Compute the Christoffel symbol.
sage: var('r t theta phi')
(r, t, theta, phi)
sage: m = matrix(SR, [[(1-1/r),0,0,0],[0,-(1-1/r)^(-1),0,0],[0,0,-r^2,0],[0,0,0,-r^2*(sin(theta))^2]])
sage: print m
[ -1/r + 1 0 0 0]
[ 0 1/(1/r - 1) 0 0]
[ 0 0 -r^2 0]
[ 0 0 0 -r^2*sin(theta)^2]
sage: def christoffel(i,j,k,vars,g):
... s = 0
... ginv = g^(-1)
... for l in range(g.nrows()):
... s = s + (1/2)*ginv[k,l]*(g[j,l].diff(vars[i])+g[i,l].diff(vars[j])-g[i,j].diff(vars[l]))
... return s
sage: christoffel(3,3,2, [t,r,theta,phi], m)
-sin(theta)*cos(theta)
sage: X = christoffel(1,1,1,[t,r,theta,phi],m)
sage: X
1/2/((1/r - 1)*r^2)
sage: X.rational_simplify()
-1/2/(r^2 - r)
Some basic things:
sage: f(x,y) = x^3 + sinh(1/y)
sage: f
(x, y) |--> x^3 + sinh(1/y)
sage: f^3
(x, y) |--> (x^3 + sinh(1/y))^3
sage: (f^3).expand()
(x, y) |--> x^9 + 3*x^6*sinh(1/y) + 3*x^3*sinh(1/y)^2 + sinh(1/y)^3
A polynomial over a symbolic base ring:
sage: R = SR[x]
sage: f = R([1/sqrt(2), 1/(4*sqrt(2))])
sage: f
1/8*sqrt(2)*x + 1/2*sqrt(2)
sage: -f
-1/8*sqrt(2)*x - 1/2*sqrt(2)
sage: (-f).degree()
1
A big product. Notice that simplifying simplifies the product further:
sage: A = exp(I*pi/5)
sage: b = A*A*A*A*A*A*A*A*A*A
sage: b
1
We check a statement made at the beginning of Friedlander and Joshi’s book on Distributions:
sage: f(x) = sin(x^2)
sage: g(x) = cos(x) + x^3
sage: u = f(x+t) + g(x-t)
sage: u
-(t - x)^3 + sin((t + x)^2) + cos(-t + x)
sage: u.diff(t,2) - u.diff(x,2)
0
Restoring variables after they have been turned into functions:
sage: x = function('x')
sage: type(x)
<class 'sage.symbolic.function_factory.NewSymbolicFunction'>
sage: x(2/3)
x(2/3)
sage: restore('x')
sage: sin(x).variables()
(x,)
MATHEMATICA: Some examples of integration and differentiation taken from some Mathematica docs:
sage: var('x n a')
(x, n, a)
sage: diff(x^n, x) # the output looks funny, but is correct
n*x^(n - 1)
sage: diff(x^2 * log(x+a), x)
2*x*log(a + x) + x^2/(a + x)
sage: derivative(arctan(x), x)
1/(x^2 + 1)
sage: derivative(x^n, x, 3)
(n - 2)*(n - 1)*n*x^(n - 3)
sage: derivative( function('f')(x), x)
D[0](f)(x)
sage: diff( 2*x*f(x^2), x)
4*x^2*D[0](f)(x^2) + 2*f(x^2)
sage: integrate( 1/(x^4 - a^4), x)
1/4*log(-a + x)/a^3 - 1/4*log(a + x)/a^3 - 1/2*arctan(x/a)/a^3
sage: expand(integrate(log(1-x^2), x))
x*log(-x^2 + 1) - 2*x - log(x - 1) + log(x + 1)
sage: integrate(log(1-x^2)/x, x)
log(-x^2 + 1)*log(x) + 1/2*polylog(2, -x^2 + 1)
sage: integrate(exp(1-x^2),x)
1/2*sqrt(pi)*e*erf(x)
sage: integrate(sin(x^2),x)
1/8*((I - 1)*sqrt(2)*erf((1/2*I - 1/2)*sqrt(2)*x) + (I + 1)*sqrt(2)*erf((1/2*I + 1/2)*sqrt(2)*x))*sqrt(pi)
sage: integrate((1-x^2)^n,x)
integrate((-x^2 + 1)^n, x)
sage: integrate(x^x,x)
integrate(x^x, x)
sage: integrate(1/(x^3+1),x)
1/3*sqrt(3)*arctan(1/3*(2*x - 1)*sqrt(3)) + 1/3*log(x + 1) - 1/6*log(x^2 - x + 1)
sage: integrate(1/(x^3+1), x, 0, 1)
1/9*pi*sqrt(3) + 1/3*log(2)
sage: forget()
sage: c = var('c')
sage: assume(c > 0)
sage: integrate(exp(-c*x^2), x, -oo, oo)
sqrt(pi)/sqrt(c)
sage: forget()
The following are a bunch of examples of integrals that Mathematica can do, but Sage currently can’t do:
sage: integrate(sqrt(x + sqrt(x)), x) # todo -- Mathematica can do this
integrate(sqrt(x + sqrt(x)), x)
sage: integrate(log(x)*exp(-x^2), x) # todo -- Mathematica can do this
integrate(e^(-x^2)*log(x), x)
Todo - Mathematica can do this and gets 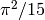 .
.
sage: integrate(log(1+sqrt(1+4*x)/2)/x, x, 0, 1) # not tested
...
ValueError: Integral is divergent.
sage: integrate(ceil(x^2 + floor(x)), x, 0, 5) # todo: Mathematica can do this
integrate(ceil(x^2) + floor(x), x, 0, 5)
MAPLE: The basic differentiation and integration examples in the Maple documentation:
sage: diff(sin(x), x)
cos(x)
sage: diff(sin(x), y)
0
sage: diff(sin(x), x, 3)
-cos(x)
sage: diff(x*sin(cos(x)), x)
-x*sin(x)*cos(cos(x)) + sin(cos(x))
sage: diff(tan(x), x)
tan(x)^2 + 1
sage: f = function('f'); f
f
sage: diff(f(x), x)
D[0](f)(x)
sage: diff(f(x,y), x, y)
D[0, 1](f)(x, y)
sage: diff(f(x,y), x, y) - diff(f(x,y), y, x)
0
sage: g = function('g')
sage: var('x y z')
(x, y, z)
sage: diff(g(x,y,z), x,z,z)
D[0, 2, 2](g)(x, y, z)
sage: integrate(sin(x), x)
-cos(x)
sage: integrate(sin(x), x, 0, pi)
2
sage: var('a b')
(a, b)
sage: integrate(sin(x), x, a, b)
cos(a) - cos(b)
sage: integrate( x/(x^3-1), x)
1/3*sqrt(3)*arctan(1/3*(2*x + 1)*sqrt(3)) + 1/3*log(x - 1) - 1/6*log(x^2 + x + 1)
sage: integrate(exp(-x^2), x)
1/2*sqrt(pi)*erf(x)
sage: integrate(exp(-x^2)*log(x), x) # todo: maple can compute this exactly.
integrate(e^(-x^2)*log(x), x)
sage: f = exp(-x^2)*log(x)
sage: f.nintegral(x, 0, 999)
(-0.87005772672831..., 7.5584...e-10, 567, 0)
sage: integral(1/sqrt(2*t^4 - 3*t^2 - 2), t, 2, 3) # todo: maple can do this
integrate(1/sqrt(2*t^4 - 3*t^2 - 2), t, 2, 3)
sage: integral(integral(x*y^2, x, 0, y), y, -2, 2)
32/5
We verify several standard differentiation rules:
sage: function('f, g')
(f, g)
sage: diff(f(t)*g(t),t)
f(t)*D[0](g)(t) + g(t)*D[0](f)(t)
sage: diff(f(t)/g(t), t)
-f(t)*D[0](g)(t)/g(t)^2 + D[0](f)(t)/g(t)
sage: diff(f(t) + g(t), t)
D[0](f)(t) + D[0](g)(t)
sage: diff(c*f(t), t)
c*D[0](f)(t)