Various parts of schemes were implemented by David Kohel, David Joyner, and William Stein.
AUTHORS:
Scheme: A scheme whose datatype might be not be defined in terms of algebraic equations: e.g. the Jacobian of a curve may be represented by means of a Scheme.
AlgebraicScheme: A scheme defined by means of polynomial equations, which may be reducible or defined over a ring other than a field. In particular, the defining ideal need not be a radical ideal, and an algebraic scheme may be defined over Spec(R).
AmbientSpaces: Most effective models of algebraic scheme will be defined, not by generic gluings, but by embeddings in some fixed ambient space.
AffineSpace: Affine spaces, and their affine subschemes form the most important universal objects from which algebraic schemes are built. The affine spaces form universal objects in the sense that a morphism is uniquely determined by the images of its coordinate functions and any such images determine a well-defined morphism.
By default affine spaces will embed in some ordinary projective space, unless it is created as an affine patch of another object.
ProjectiveSpace: The projective spaces are the most natural ambient spaces for most projective objects. They are locally universal objects.
ProjectiveSpace_ordinary (not implemented)
The ordinary projective spaces have the standard weights ![[1,..,1]](../../_images/math/af0f4c34a15ad888fa89ce66e4afd2f6a2bd8369.png) on their coefficients.
on their coefficients.
ProjectiveSpace_weighted (not implemented): A special subtype for non-standard weights.
ToricSpace (not implemented): This defines a projective toric variety, which defines a space equipped with a toral action and certain defining data. These generalise projective spaces, but it is not envisioned that the latter should inherit from the ToricSpace type.
AlgebraicScheme_subscheme_affine: An algebraic scheme defined by means of an embedding in a fixed ambient affine space.
AlgebraicScheme_subscheme_projective: An algebraic scheme defined by means of an embedding in a fixed ambient projective space.
QuasiAffineScheme (not yet implemented):
An open subset 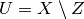 of a closed subset
of a closed subset  of affine space; note
that this is mathematically a quasi-projective scheme, but its
ambient space is an affine space and its points are represented by
affine rather than projective points.
of affine space; note
that this is mathematically a quasi-projective scheme, but its
ambient space is an affine space and its points are represented by
affine rather than projective points.
Note
AlgebraicScheme_quasi is implemented, as a base class for this.
QuasiProjectiveScheme (not yet implemented):
An open subset of a closed subset of projective space; this datatype
stores the defining polynomial, polynomials, or ideal defining the
projective closure  plus the closed subscheme
plus the closed subscheme 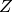 of
of  whose complement
whose complement
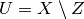 is the quasi-projective scheme.
is the quasi-projective scheme.
Note: the quasi-affine and quasi-projective datatype lets one create
schemes like the multiplicative group scheme  and the non-affine scheme
and the non-affine scheme 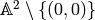 . The
latter is not affine and is not of the form
. The
latter is not affine and is not of the form 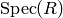 .
.
PointSets and points over a ring:
For algebraic schemes 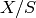 and
and  over
over 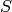 , one can form
the point set
, one can form
the point set  of morphisms from
of morphisms from  over
over 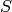 .
.
sage: PP.<X,Y,Z> = ProjectiveSpace(2, QQ)
sage: PP
Projective Space of dimension 2 over Rational Field
The last line is an abuse of language – returning the generators of the coordinate ring by gens().
A projective space object in the category of schemes is a locally
free object – the images of the generator functions locally
determine a point. Over a field, one can choose one of the standard
affine patches by the condition that a coordinate function 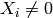
sage: PP(QQ)
Set of Rational Points of Projective Space of dimension 2 over Rational Field
sage: PP(QQ)([-2,3,5])
(-2/5 : 3/5 : 1)
Over a ring, this is not true, e.g. even over an integral domain which is not a PID, there may be no single affine patch which covers a point.
sage: R.<x> = ZZ[]
sage: S.<t> = R.quo(x^2+5)
sage: P.<X,Y,Z> = ProjectiveSpace(2, S)
sage: P(S)
Set of Rational Points of Projective Space of dimension 2 over
Univariate Quotient Polynomial Ring in t over Integer Ring with
modulus x^2 + 5
In order to represent the projective point 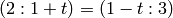 we
note that the first representative is not well-defined at the
prime
we
note that the first representative is not well-defined at the
prime 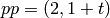 and the second element is not well-defined at
the prime
and the second element is not well-defined at
the prime 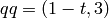 , but that
, but that 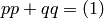 , so globally the
pair of coordinate representatives is well-defined.
, so globally the
pair of coordinate representatives is well-defined.
sage: P( [2, 1+t] )
...
NotImplementedError
In fact, we need a test R.ideal([2,1+t]) == R.ideal([1]) in order to make this meaningful.