AUTHORS:
- William Stein (August 2009)– most of the initial version
- Robert Bradshaw (July 2009) – an early version of some specific code
EXAMPLES:
sage: E = EllipticCurve('433a')
sage: P = E.heegner_point(-8,3)
sage: z = P.point_exact(200); z
(-4/3 : 1/27*a - 4/27 : 1)
sage: parent(z)
Abelian group of points on Elliptic Curve defined by y^2 + x*y = x^3 + 1 over Number Field in a with defining polynomial x^2 - 44*x + 1159
sage: parent(z[0]).discriminant()
-3
sage: E.quadratic_twist(-3).rank()
1
sage: K.<a> = QuadraticField(-8)
sage: K.factor(3)
(Fractional ideal (1/2*a + 1)) * (Fractional ideal (-1/2*a + 1))
Next try an inert prime:
sage: K.factor(5)
Fractional ideal (5)
sage: P = E.heegner_point(-8,5)
sage: z = P.point_exact(300)
sage: z[0].charpoly().factor()
(x^6 + x^5 - 1/4*x^4 + 19/10*x^3 + 31/20*x^2 - 7/10*x + 49/100)^2
sage: z[1].charpoly().factor()
x^12 - x^11 + 6/5*x^10 - 33/40*x^9 - 89/320*x^8 + 3287/800*x^7 - 5273/1600*x^6 + 993/4000*x^5 + 823/320*x^4 - 2424/625*x^3 + 12059/12500*x^2 + 3329/25000*x + 123251/250000
sage: f = P.x_poly_exact(300); f
x^6 + x^5 - 1/4*x^4 + 19/10*x^3 + 31/20*x^2 - 7/10*x + 49/100
sage: f.discriminant().factor()
-1 * 2^-9 * 5^-9 * 7^2 * 281^2 * 1021^2
We find some Mordell-Weil generators in the rank 1 case using Heegner points:
sage: E = EllipticCurve('43a'); P = E.heegner_point(-7)
sage: P.x_poly_exact()
x
sage: P.point_exact()
(0 : 0 : 1)
sage: E = EllipticCurve('997a')
sage: E.rank()
1
sage: E.heegner_discriminants_list(10)
[-19, -23, -31, -35, -39, -40, -52, -55, -56, -59]
sage: P = E.heegner_point(-19)
sage: P.x_poly_exact()
x - 141/49
sage: P.point_exact()
(141/49 : -162/343 : 1)
Here we find that the Heegner point generates a subgroup of index 3:
sage: E = EllipticCurve('92b1')
sage: E.heegner_discriminants_list(1)
[-7]
sage: P = E.heegner_point(-7); z = P.point_exact(); z
(0 : 1 : 1)
sage: E.regulator()
0.0498083972980648
sage: z.height()
0.448275575682583
sage: P = E(1,1); P # a generator
(1 : 1 : 1)
sage: -3*P
(0 : 1 : 1)
sage: E.tamagawa_product()
3
The above is consistent with the following analytic computation:
sage: E.heegner_index(-7)
3.0000?
Bases: sage.structure.sage_object.SageObject
An abstract automorphism of a ring class field.
Return the domain of this automorphism.
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: s = E.heegner_point(-7,5).ring_class_field().galois_group().complex_conjugation()
sage: s.domain()
Ring class field extension of QQ[sqrt(-7)] of conductor 5
Return the parent of this automorphism, which is a Galois group of a ring class field.
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: s = E.heegner_point(-7,5).ring_class_field().galois_group().complex_conjugation()
sage: s.parent()
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 5
Bases: sage.schemes.elliptic_curves.heegner.GaloisAutomorphism
The complex conjugation automorphism of a ring class field.
EXAMPLES:
sage: conj = heegner_point(37,-7,5).ring_class_field().galois_group().complex_conjugation()
sage: conj
Complex conjugation automorphism of Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: conj.domain()
Ring class field extension of QQ[sqrt(-7)] of conductor 5
TESTS:
sage: type(conj)
<class 'sage.schemes.elliptic_curves.heegner.GaloisAutomorphismComplexConjugation'>
sage: loads(dumps(conj)) == conj
True
EXAMPLES:
sage: conj = heegner_point(37,-7,5).ring_class_field().galois_group().complex_conjugation()
sage: conj.order()
2
Bases: sage.schemes.elliptic_curves.heegner.GaloisAutomorphism
An automorphism of a ring class field defined by a quadratic form.
EXAMPLES:
sage: H = heegner_points(389,-20,3)
sage: sigma = H.ring_class_field().galois_group(H.quadratic_field())[0]; sigma
Class field automorphism defined by x^2 + 45*y^2
sage: type(sigma)
<class 'sage.schemes.elliptic_curves.heegner.GaloisAutomorphismQuadraticForm'>
sage: loads(dumps(sigma)) == sigma
True
Optional data that specified element corresponding element of
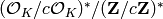 , via class
field theory.
, via class
field theory.
This is a generator of the ideal corresponding to this automorphism.
EXAMPLES:
sage: K3 = heegner_points(389,-52,3).ring_class_field()
sage: K1 = heegner_points(389,-52,1).ring_class_field()
sage: G = K3.galois_group(K1)
sage: orb = sorted([g.alpha() for g in G]); orb # random (the sign depends on the database being installed or not)
[1, 1/2*sqrt_minus_52 + 1, -1/2*sqrt_minus_52, 1/2*sqrt_minus_52 - 1]
sage: [x^2 for x in orb] # this is just for testing
[1, sqrt_minus_52 - 12, -13, -sqrt_minus_52 - 12]
sage: K5 = heegner_points(389,-52,5).ring_class_field()
sage: K1 = heegner_points(389,-52,1).ring_class_field()
sage: G = K5.galois_group(K1)
sage: orb = sorted([g.alpha() for g in G]); orb # random (the sign depends on the database being installed or not)
[1, -1/2*sqrt_minus_52, 1/2*sqrt_minus_52 + 1, 1/2*sqrt_minus_52 - 1, 1/2*sqrt_minus_52 - 2, -1/2*sqrt_minus_52 - 2]
sage: [x^2 for x in orb] # just for testing
[1, -13, sqrt_minus_52 - 12, -sqrt_minus_52 - 12, -2*sqrt_minus_52 - 9, 2*sqrt_minus_52 - 9]
Return ideal of ring of integers of quadratic imaginary field corresponding to this quadratic form. This is the ideal
.
EXAMPLES:
sage: E = EllipticCurve('389a'); F= E.heegner_point(-20,3).ring_class_field()
sage: G = F.galois_group(F.quadratic_field())
sage: G[1].ideal()
Fractional ideal (2, -1/2*sqrt_minus_20 + 1)
sage: [s.ideal().gens() for s in G]
[(1, 3/2*sqrt_minus_20), (2, 3/2*sqrt_minus_20 - 1), (5, 3/2*sqrt_minus_20), (7, 3/2*sqrt_minus_20 - 2)]
Return the multiplicative order of this Galois group automorphism.
EXAMPLES:
sage: K3 = heegner_points(389,-52,3).ring_class_field()
sage: K1 = heegner_points(389,-52,1).ring_class_field()
sage: G = K3.galois_group(K1)
sage: sorted([g.order() for g in G])
[1, 2, 4, 4]
sage: K5 = heegner_points(389,-52,5).ring_class_field()
sage: K1 = heegner_points(389,-52,1).ring_class_field()
sage: G = K5.galois_group(K1)
sage: sorted([g.order() for g in G])
[1, 2, 3, 3, 6, 6]
Return element of the projective line corresponding to this automorphism.
This only makes sense if this automorphism is in the Galois
group 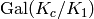 .
.
EXAMPLES:
sage: K3 = heegner_points(389,-52,3).ring_class_field()
sage: K1 = heegner_points(389,-52,1).ring_class_field()
sage: G = K3.galois_group(K1)
sage: sorted([g.p1_element() for g in G])
[(0, 1), (1, 0), (1, 1), (1, 2)]
sage: K5 = heegner_points(389,-52,5).ring_class_field()
sage: K1 = heegner_points(389,-52,1).ring_class_field()
sage: G = K5.galois_group(K1)
sage: sorted([g.p1_element() for g in G])
[(0, 1), (1, 0), (1, 1), (1, 2), (1, 3), (1, 4)]
Return reduced quadratic form corresponding to this Galois automorphism.
EXAMPLES:
sage: H = heegner_points(389,-20,3); s = H.ring_class_field().galois_group(H.quadratic_field())[0]
sage: s.quadratic_form()
x^2 + 45*y^2
Bases: sage.structure.sage_object.SageObject
A Galois group of a ring class field.
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: G = E.heegner_point(-7,5).ring_class_field().galois_group(); G
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: G.field()
Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: G.cardinality()
12
sage: G.complex_conjugation()
Complex conjugation automorphism of Ring class field extension of QQ[sqrt(-7)] of conductor 5
TESTS:
sage: G = heegner_point(37,-7).ring_class_field().galois_group()
sage: loads(dumps(G)) == G
True
sage: type(G)
<class 'sage.schemes.elliptic_curves.heegner.GaloisGroup'>
Return the base field, which the field fixed by all the automorphisms in this Galois group.
EXAMPLES:
sage: x = heegner_point(37,-7,5)
sage: Kc = x.ring_class_field(); Kc
Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: K = x.quadratic_field()
sage: G = Kc.galois_group(); G
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: G.base_field()
Rational Field
sage: G.cardinality()
12
sage: Kc.absolute_degree()
12
sage: G = Kc.galois_group(K); G
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 5 over Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
sage: G.cardinality()
6
sage: G.base_field()
Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
sage: G = Kc.galois_group(Kc); G
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 5 over Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: G.cardinality()
1
sage: G.base_field()
Ring class field extension of QQ[sqrt(-7)] of conductor 5
Return the cardinality of this Galois group.
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: G = E.heegner_point(-7,5).ring_class_field().galois_group(); G
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: G.cardinality()
12
sage: G = E.heegner_point(-7).ring_class_field().galois_group()
sage: G.cardinality()
2
sage: G = E.heegner_point(-7,55).ring_class_field().galois_group()
sage: G.cardinality()
120
Return the automorphism of self determined by complex conjugation. The base field must be the rational numbers.
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: G = E.heegner_point(-7,5).ring_class_field().galois_group()
sage: G.complex_conjugation()
Complex conjugation automorphism of Ring class field extension of QQ[sqrt(-7)] of conductor 5
Return the ring class field that this Galois group acts on.
EXAMPLES:
sage: G = heegner_point(389,-7,5).ring_class_field().galois_group()
sage: G.field()
Ring class field extension of QQ[sqrt(-7)] of conductor 5
Return True if conductor  is prime to the discriminant of the
quadratic field,
is prime to the discriminant of the
quadratic field,  is squarefree and each prime dividing
is squarefree and each prime dividing  is inert.
is inert.
EXAMPLES:
sage: K5 = heegner_points(389,-52,5).ring_class_field()
sage: K1 = heegner_points(389,-52,1).ring_class_field()
sage: K5.galois_group(K1).is_kolyvagin()
True
sage: K7 = heegner_points(389,-52,7).ring_class_field()
sage: K7.galois_group(K1).is_kolyvagin()
False
sage: K25 = heegner_points(389,-52,25).ring_class_field()
sage: K25.galois_group(K1).is_kolyvagin()
False
Assuming this Galois group 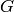 is of the form
is of the form
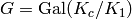 , with
, with 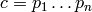 satisfying the
Kolyvagin hypothesis, this function returns noncanonical
choices of lifts of generators for each of the cyclic factors
of
satisfying the
Kolyvagin hypothesis, this function returns noncanonical
choices of lifts of generators for each of the cyclic factors
of 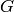 corresponding to the primes dividing
corresponding to the primes dividing  . Thus the
. Thus the
 -th returned valued is an element of
-th returned valued is an element of 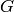 that maps to the
identity element of
that maps to the
identity element of  for all
for all 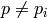 and
to a choice of generator of
and
to a choice of generator of 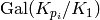 .
.
OUTPUT:
- list of elements of self
EXAMPLES:
sage: K3 = heegner_points(389,-52,3).ring_class_field()
sage: K1 = heegner_points(389,-52,1).ring_class_field()
sage: G = K3.galois_group(K1)
sage: G.kolyvagin_generators()
(Class field automorphism defined by 9*x^2 - 6*x*y + 14*y^2,)
sage: K5 = heegner_points(389,-52,5).ring_class_field()
sage: K1 = heegner_points(389,-52,1).ring_class_field()
sage: G = K5.galois_group(K1)
sage: G.kolyvagin_generators()
(Class field automorphism defined by 17*x^2 - 14*x*y + 22*y^2,)
Assuming this Galois group 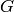 is of the form
is of the form 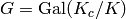 ,
this function returns noncanonical choices of lifts of the
elements of the quotient group
,
this function returns noncanonical choices of lifts of the
elements of the quotient group 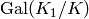 .
.
OUTPUT:
- tuple of elements of self
EXAMPLES:
sage: K5 = heegner_points(389,-52,5).ring_class_field()
sage: G = K5.galois_group(K5.quadratic_field())
sage: G.lift_of_hilbert_class_field_galois_group()
(Class field automorphism defined by x^2 + 325*y^2, Class field automorphism defined by 2*x^2 + 2*x*y + 163*y^2)
sage: G.cardinality()
12
sage: K5.quadratic_field().class_number()
2
Bases: sage.structure.sage_object.SageObject
A Heegner point of level  , discriminant
, discriminant  and conductor
and conductor  is any point on a modular curve or elliptic curve that is
concocted in some way from a quadratic imaginary
is any point on a modular curve or elliptic curve that is
concocted in some way from a quadratic imaginary 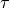 in the upper
half plane with
in the upper
half plane with 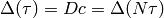 .
.
EXAMPLES:
sage: x = sage.schemes.elliptic_curves.heegner.HeegnerPoint(389,-7,13); x
Heegner point of level 389, discriminant -7, and conductor 13
sage: type(x)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerPoint'>
sage: loads(dumps(x)) == x
True
Return the conductor of this Heegner point.
EXAMPLES:
sage: heegner_point(389,-7,5).conductor()
5
sage: E = EllipticCurve('37a1'); P = E.kolyvagin_point(-67,7); P
Kolyvagin point of discriminant -67 and conductor 7 on elliptic curve of conductor 37
sage: P.conductor()
7
sage: E = EllipticCurve('389a'); P = E.heegner_point(-7, 5); P.conductor()
5
Return the discriminant of the quadratic imaginary field associated to this Heegner point.
EXAMPLES:
sage: heegner_point(389,-7,5).discriminant()
-7
sage: E = EllipticCurve('37a1'); P = E.kolyvagin_point(-67,7); P
Kolyvagin point of discriminant -67 and conductor 7 on elliptic curve of conductor 37
sage: P.discriminant()
-67
sage: E = EllipticCurve('389a'); P = E.heegner_point(-7, 5); P.discriminant()
-7
Return the level of this Heegner point, which is the level of the
modular curve 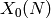 on which this is a Heegner point.
on which this is a Heegner point.
EXAMPLES:
sage: heegner_point(389,-7,5).level()
389
Return the quadratic number field of discriminant  .
.
EXAMPLES:
sage: x = heegner_point(37,-7,5)
sage: x.quadratic_field()
Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
sage: E = EllipticCurve('37a'); P = E.heegner_point(-40)
sage: P.quadratic_field()
Number Field in sqrt_minus_40 with defining polynomial x^2 + 40
sage: P.quadratic_field() is P.quadratic_field()
True
sage: type(P.quadratic_field())
<class 'sage.rings.number_field.number_field.NumberField_quadratic_with_category'>
Return the order in the quadratic imaginary field of conductor
 , where
, where  is the conductor of this Heegner point.
is the conductor of this Heegner point.
EXAMPLES:
sage: heegner_point(389,-7,5).quadratic_order()
Order in Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
sage: heegner_point(389,-7,5).quadratic_order().basis()
[1, 5*sqrt_minus_7]
sage: E = EllipticCurve('37a'); P = E.heegner_point(-40,11)
sage: P.quadratic_order()
Order in Number Field in sqrt_minus_40 with defining polynomial x^2 + 40
sage: P.quadratic_order().basis()
[1, 11*sqrt_minus_40]
Return the ring class field associated to this Heegner point.
This is an extension  over
over  , where
, where  is the
quadratic imaginary field and
is the
quadratic imaginary field and  is the conductor associated
to this Heegner point. This Heegner point is defined over
is the conductor associated
to this Heegner point. This Heegner point is defined over
 and the Galois group
and the Galois group 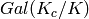 acts transitively on
the Galois conjugates of this Heegner point.
acts transitively on
the Galois conjugates of this Heegner point.
EXAMPLES:
sage: E = EllipticCurve('389a'); K.<a> = QuadraticField(-5)
sage: len(K.factor(5))
1
sage: len(K.factor(23))
2
sage: E.heegner_point(-7, 5).ring_class_field().degree_over_K()
6
sage: E.heegner_point(-7, 23).ring_class_field().degree_over_K()
22
sage: E.heegner_point(-7, 5*23).ring_class_field().degree_over_K()
132
sage: E.heegner_point(-7, 5^2).ring_class_field().degree_over_K()
...
NotImplementedError: degree only implemented when c squarefree
sage: E.heegner_point(-7, 7).ring_class_field().degree_over_K()
...
ValueError: conductor and discriminant must be coprime
Bases: sage.schemes.elliptic_curves.heegner.HeegnerPoint
A Heegner point on a curve associated to an order in a quadratic imaginary field.
EXAMPLES:
sage: E = EllipticCurve('37a'); P = E.heegner_point(-7,5); P
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 37
sage: type(P)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerPointOnEllipticCurve'>
Return the 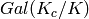 conjugates of this Heegner point.
conjugates of this Heegner point.
EXAMPLES:
sage: E = EllipticCurve('77a')
sage: y = E.heegner_point(-52,5); y
Heegner point of discriminant -52 and conductor 5 on elliptic curve of conductor 77
sage: print [z.quadratic_form() for z in y.conjugates_over_K()]
[77*x^2 + 52*x*y + 13*y^2, 154*x^2 + 206*x*y + 71*y^2, 539*x^2 + 822*x*y + 314*y^2, 847*x^2 + 1284*x*y + 487*y^2, 1001*x^2 + 52*x*y + y^2, 1078*x^2 + 822*x*y + 157*y^2, 1309*x^2 + 360*x*y + 25*y^2, 1309*x^2 + 2054*x*y + 806*y^2, 1463*x^2 + 976*x*y + 163*y^2, 2233*x^2 + 2824*x*y + 893*y^2, 2387*x^2 + 2054*x*y + 442*y^2, 3619*x^2 + 3286*x*y + 746*y^2]
sage: y.quadratic_form()
77*x^2 + 52*x*y + 13*y^2
Return the elliptic curve on which this is a Heegner point.
EXAMPLES:
sage: E = EllipticCurve('389a'); P = E.heegner_point(-7, 5)
sage: P.curve()
Elliptic Curve defined by y^2 + y = x^3 + x^2 - 2*x over Rational Field
sage: P.curve() is E
True
Return Heegner point on 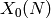 that maps to this Heegner point on
that maps to this Heegner point on  .
.
EXAMPLES:
sage: E = EllipticCurve('37a'); P = E.heegner_point(-7,5); P
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 37
sage: P.heegner_point_on_X0N()
Heegner point 5/74*sqrt(-7) - 11/74 of discriminant -7 and conductor 5 on X_0(37)
Return the Kolyvagin class associated to this Heegner point.
INPUT:
– positive integer that divides the gcd of
and
for all
dividing the conductor. If
is None, choose the largest valid
.
EXAMPLES:
sage: y = EllipticCurve('389a').heegner_point(-7,5)
sage: y.kolyvagin_cohomology_class(3)
Kolyvagin cohomology class c(5) in H^1(K,E[3])
Return the Kolyvagin point corresponding to this Heegner
point. This is the point obtained by applying the Kolyvagin
operator 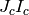 in the group ring of the Galois group to
this Heegner point. It is a point that defines an element
of
in the group ring of the Galois group to
this Heegner point. It is a point that defines an element
of ![H^1(K, E[n])](../../../_images/math/5c2fac7152fb59d5458c3c52f9d3cfe49c8e3c0f.png) , under certain hypotheses on
, under certain hypotheses on  .
.
EXAMPLES:
sage: E = EllipticCurve('37a1'); y = E.heegner_point(-7); y
Heegner point of discriminant -7 on elliptic curve of conductor 37
sage: P = y.kolyvagin_point(); P
Kolyvagin point of discriminant -7 on elliptic curve of conductor 37
sage: P.numerical_approx()
(-3.4...e-16 - 2.00...e-16*I : 3.4...e-16 + 2.000...e-16*I : 1.00000000000000)
Return the point in the subfield 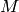 of the complex numbers
(well defined only modulo the period lattice) corresponding to
this Heegner point.
of the complex numbers
(well defined only modulo the period lattice) corresponding to
this Heegner point.
EXAMPLES:
We compute a nonzero Heegner point over a ring class field on a curve of rank 2:
sage: E = EllipticCurve('389a'); y = E.heegner_point(-7,5)
sage: y.map_to_complex_numbers()
1.49979679635196 + 0.369156204821526*I
sage: y.map_to_complex_numbers(100)
1.4997967963519640592142411892 + 0.36915620482152626830089145962*I
sage: y.map_to_complex_numbers(10)
1.5 + 0.37*I
Here we see that the Heegner point is 0 since it lies in the lattice:
sage: E = EllipticCurve('389a'); y = E.heegner_point(-7)
sage: y.map_to_complex_numbers(10)
0.0034 - 3.9*I
sage: y.map_to_complex_numbers()
4.71844785465692e-15 - 3.94347540310330*I
sage: E.period_lattice().basis()
(2.49021256085505, 1.97173770155165*I)
sage: 2*E.period_lattice().basis()[1]
3.94347540310330*I
You can also directly coerce to the complex field:
sage: E = EllipticCurve('389a'); y = E.heegner_point(-7)
sage: ComplexField(100)(y)
-8.6774699574311298595290142181e-30 - 3.9434754031032964088448153963*I
Return a numerical approximation to this Heegner point computed using a working precision of prec bits.
Warning
The answer is not provably correct to prec bits! A priori, due to rounding and other errors, it’s possible that not a single digit is correct.
INPUT:
- prec – (default: None) the working precision
EXAMPLES:
sage: E = EllipticCurve('37a'); P = E.heegner_point(-7); P
Heegner point of discriminant -7 on elliptic curve of conductor 37
sage: P.numerical_approx()
(-3.41...e-16 - 2.000...e-16*I : 3.42...e-16 + 2.00...e-16*I : 1.00000000000000)
sage: P.numerical_approx(10)
(0.0030 - 0.0028*I : -0.0030 + 0.0028*I : 1.0)
sage: P.numerical_approx(100)[0]
8.4419827889841225189186778139e-31 + 6.0876...e-31*I
sage: E = EllipticCurve('37a'); P = E.heegner_point(-40); P
Heegner point of discriminant -40 on elliptic curve of conductor 37
sage: P.numerical_approx()
(-6.68...e-16 + 1.41421356237310*I : 1.00000000000000 - 1.41421356237309*I : 1.00000000000000)
A rank 2 curve, where all Heegner points of conductor 1 are 0:
sage: E = EllipticCurve('389a'); E.rank()
2
sage: P = E.heegner_point(-7); P
Heegner point of discriminant -7 on elliptic curve of conductor 389
sage: P.numerical_approx()
(4.08580183114324e28 + 1.50348132882460e28*I : -7.84283601876376e42 - 4.58366020722762e42*I : 1.00000000000000) # 64-bit
(0 : 1.00000000000000 : 0) # 32-bit
sage: P.numerical_approx(70)
(0 : 1.0000000000000000000 : 0)
However, Heegner points of bigger conductor are often nonzero:
sage: E = EllipticCurve('389a'); P = E.heegner_point(-7, 5); P
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 389
sage: P.numerical_approx()
(0.6755075569268... + 0.3447496493026...*I : -0.3771429314018... + 0.8433662271371...*I : 1.00000000000000)
sage: E.heegner_point(-7, 11).numerical_approx()
(0.1795583794118... + 0.02035501750912...*I : -0.5573941377055... + 0.2738940831635...*I : 1.00000000000000)
sage: E.heegner_point(-7, 13).numerical_approx()
(1.034302915374... - 3.302744319777...*I : 1.323937875767... + 6.908264226850...*I : 1.00000000000000)
We find (probably) the definining polynomial of the
 -coordinate of
-coordinate of 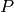 , which defines a class field. The shape of
the discriminant below is strong confirmation – but not proof
– that this polynomial is correct:
, which defines a class field. The shape of
the discriminant below is strong confirmation – but not proof
– that this polynomial is correct:
sage: f = P.numerical_approx(70)[0].algdep(6); f
1225*x^6 + 1750*x^5 - 21675*x^4 - 380*x^3 + 110180*x^2 - 129720*x + 48771
sage: f.discriminant().factor()
2^6 * 3^2 * 5^11 * 7^4 * 13^2 * 19^6 * 199^2 * 719^2 * 26161^2
Return exact point on the elliptic curve over a number field defined by computing this Heegner point to the given number of bits of precision. A ValueError is raised if the precision is clearly insignificant to define a point on the curve.
Warning
It is in theory possible for this function to not raise a ValueError, find a point on the curve, but via some very unlikely coincidence that point is not actually this Heegner point.
Warning
Currently we make an arbitrary choice of 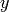 -coordinate for
the lift of the
-coordinate for
the lift of the  -coordinate.
-coordinate.
INPUT:
- prec – integer (default: 53)
- algorithm – see the description of the algorithm parameter for the exact_x_poly method.
- var – string (default: ‘a’)
- optimize – book (default; False) if True, try to optimize defining polynomial for the number field that the point is defined over. Off by default, since this can be very expensive.
EXAMPLES:
sage: E = EllipticCurve('389a'); P = E.heegner_point(-7, 5); P
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 389
sage: z = P.point_exact(100, optimize=True)
sage: z[1].charpoly()
x^12 + 6*x^11 + 90089/1715*x^10 + 71224/343*x^9 + 52563964/588245*x^8 - 483814934/588245*x^7 - 156744579/16807*x^6 - 2041518032/84035*x^5 + 1259355443184/14706125*x^4 + 3094420220918/14706125*x^3 + 123060442043827/367653125*x^2 + 82963044474852/367653125*x + 211679465261391/1838265625
sage: f = P.numerical_approx(500)[1].algdep(12); f / f.leading_coefficient()
x^12 + 6*x^11 + 90089/1715*x^10 + 71224/343*x^9 + 52563964/588245*x^8 - 483814934/588245*x^7 - 156744579/16807*x^6 - 2041518032/84035*x^5 + 1259355443184/14706125*x^4 + 3094420220918/14706125*x^3 + 123060442043827/367653125*x^2 + 82963044474852/367653125*x + 211679465261391/1838265625
Return the integral primitive positive definite binary quadratic form associated to this Heegner point.
EXAMPLES:
sage: EllipticCurve('389a').heegner_point(-7, 5).quadratic_form()
389*x^2 + 147*x*y + 14*y^2
sage: P = EllipticCurve('389a').heegner_point(-7, 5, (778,925,275)); P
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 389
sage: P.quadratic_form()
778*x^2 + 925*x*y + 275*y^2
Return True if this Heegner point and  satisfy the
Kolyvagin hypothesis, i.e., that each prime dividing the
conductor
satisfy the
Kolyvagin hypothesis, i.e., that each prime dividing the
conductor  of self is inert in K and coprime to
of self is inert in K and coprime to 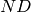 .
Moreover, if
.
Moreover, if  isn’t None, also check that for each prime
isn’t None, also check that for each prime
 dividing
dividing  we have that
we have that 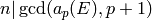 .
.
INPUT:
– positive integer
EXAMPLES:
sage: EllipticCurve('389a').heegner_point(-7).satisfies_kolyvagin_hypothesis()
True
sage: EllipticCurve('389a').heegner_point(-7,5).satisfies_kolyvagin_hypothesis()
True
sage: EllipticCurve('389a').heegner_point(-7,11).satisfies_kolyvagin_hypothesis()
False
Return 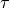 in the upper half plane that maps via the
modular parametrization to this Heegner point.
in the upper half plane that maps via the
modular parametrization to this Heegner point.
EXAMPLES:
sage: E = EllipticCurve('389a'); P = E.heegner_point(-7, 5)
sage: P.tau()
5/778*sqrt_minus_7 - 147/778
Return irreducible polynomial over the rational numbers
satisfied by the  coordinate of this Heegner point. A
ValueError is raised if the precision is clearly insignificant
to define a point on the curve.
coordinate of this Heegner point. A
ValueError is raised if the precision is clearly insignificant
to define a point on the curve.
Warning
It is in theory possible for this function to not raise a ValueError, find a polynomial, but via some very unlikely coincidence that point is not actually this Heegner point.
INPUT:
prec – integer (default: 53)
- algorithm – ‘conjugates’ (default) or ‘lll’; if
‘conjugates’, compute numerically all the conjugates y[i] of the Heegner point and construct the characteristic polynomial as the product
. If ‘lll’, compute only one of the conjugates y[0], then uses the LLL algorithm to guess
.
EXAMPLES:
We compute some  -coordinate polynomials of some conductor 1
Heegner points:
-coordinate polynomials of some conductor 1
Heegner points:
sage: E = EllipticCurve('37a')
sage: v = E.heegner_discriminants_list(10)
sage: [E.heegner_point(D).x_poly_exact() for D in v]
[x, x, x^2 + 2, x^5 - x^4 + x^3 + x^2 - 2*x + 1, x - 6, x^7 - 2*x^6 + 9*x^5 - 10*x^4 - x^3 + 8*x^2 - 5*x + 1, x^3 + 5*x^2 + 10*x + 4, x^4 - 10*x^3 + 10*x^2 + 12*x - 12, x^8 - 5*x^7 + 7*x^6 + 13*x^5 - 10*x^4 - 4*x^3 + x^2 - 5*x + 7, x^6 - 2*x^5 + 11*x^4 - 24*x^3 + 30*x^2 - 16*x + 4]
We compute  -coordinate polynomials for some Heegner points
of conductor bigger than 1 on a rank 2 curve:
-coordinate polynomials for some Heegner points
of conductor bigger than 1 on a rank 2 curve:
sage: E = EllipticCurve('389a'); P = E.heegner_point(-7, 5); P
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 389
sage: P.x_poly_exact()
...
ValueError: insufficient precision to determine Heegner point (fails discriminant test)
sage: P.x_poly_exact(75)
x^6 + 10/7*x^5 - 867/49*x^4 - 76/245*x^3 + 3148/35*x^2 - 25944/245*x + 48771/1225
sage: E.heegner_point(-7,11).x_poly_exact(300)
x^10 + 282527/52441*x^9 + 27049007420/2750058481*x^8 - 22058564794/2750058481*x^7 - 140054237301/2750058481*x^6 + 696429998952/30250643291*x^5 + 2791387923058/30250643291*x^4 - 3148473886134/30250643291*x^3 + 1359454055022/30250643291*x^2 - 250620385365/30250643291*x + 181599685425/332757076201
Here we compute a Heegner point of conductor 5 on a rank 3 curve:
sage: E = EllipticCurve('5077a'); P = E.heegner_point(-7,5); P
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 5077
sage: P.x_poly_exact(300)
x^6 + 1108754853727159228/72351048803252547*x^5 + 88875505551184048168/1953478317687818769*x^4 - 2216200271166098662132/3255797196146364615*x^3 + 14941627504168839449851/9767391588439093845*x^2 - 3456417460183342963918/3255797196146364615*x + 1306572835857500500459/5426328660243941025
Bases: sage.schemes.elliptic_curves.heegner.HeegnerPoint
A Heegner point as a point on the modular curve 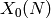 , which we
view as the upper half plane modulo the action of
, which we
view as the upper half plane modulo the action of 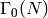 .
.
EXAMPLES:
sage: x = heegner_point(37,-7,5); x
Heegner point 5/74*sqrt(-7) - 11/74 of discriminant -7 and conductor 5 on X_0(37)
sage: type(x)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerPointOnX0N'>
sage: x.level()
37
sage: x.conductor()
5
sage: x.discriminant()
-7
sage: x.quadratic_field()
Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
sage: x.quadratic_form()
37*x^2 + 11*x*y + 2*y^2
sage: x.quadratic_order()
Order in Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
sage: x.tau()
5/74*sqrt_minus_7 - 11/74
sage: loads(dumps(x)) == x
True
Given an integer Q dividing the level N such that 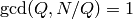 , returns the
image of this Heegner point under the Atkin-Lehner operator
, returns the
image of this Heegner point under the Atkin-Lehner operator 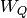 .
.
INPUT:
– positive divisor of
; if not given, default to
EXAMPLES:
sage: x = heegner_point(389,-7,5)
sage: x.atkin_lehner_act()
Heegner point 5/199168*sqrt(-7) - 631/199168 of discriminant -7 and conductor 5 on X_0(389)
sage: x = heegner_point(45,D=-11,c=1); x
Heegner point 1/90*sqrt(-11) - 13/90 of discriminant -11 on X_0(45)
sage: x.atkin_lehner_act(5)
Heegner point 1/90*sqrt(-11) + 23/90 of discriminant -11 on X_0(45)
sage: y = x.atkin_lehner_act(9); y
Heegner point 1/90*sqrt(-11) - 23/90 of discriminant -11 on X_0(45)
sage: z = y.atkin_lehner_act(9); z
Heegner point 1/90*sqrt(-11) - 13/90 of discriminant -11 on X_0(45)
sage: z == x
True
Return the 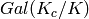 -orbit of this Heegner point.
-orbit of this Heegner point.
EXAMPLES:
sage: x = heegner_point(389,-7,3); x
Heegner point 3/778*sqrt(-7) - 223/778 of discriminant -7 and conductor 3 on X_0(389)
sage: x.galois_orbit_over_K()
[Heegner point 3/778*sqrt(-7) - 223/778 of discriminant -7 and conductor 3 on X_0(389), Heegner point 3/1556*sqrt(-7) - 223/1556 of discriminant -7 and conductor 3 on X_0(389), Heegner point 3/1556*sqrt(-7) - 1001/1556 of discriminant -7 and conductor 3 on X_0(389), Heegner point 3/3112*sqrt(-7) - 223/3112 of discriminant -7 and conductor 3 on X_0(389)]
Return the image of this Heegner point on the elliptic curve
 , which must also have conductor
, which must also have conductor  , where
, where  is the
level of self.
is the
level of self.
EXAMPLES:
sage: x = heegner_point(389,-7,5); x
Heegner point 5/778*sqrt(-7) - 147/778 of discriminant -7 and conductor 5 on X_0(389)
sage: y = x.map_to_curve(EllipticCurve('389a')); y
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 389
sage: y.curve().cremona_label()
'389a1'
sage: y.heegner_point_on_X0N()
Heegner point 5/778*sqrt(-7) - 147/778 of discriminant -7 and conductor 5 on X_0(389)
You can also directly apply the modular parametrization of the elliptic curve:
sage: x = heegner_point(37,-7); x
Heegner point 1/74*sqrt(-7) - 17/74 of discriminant -7 on X_0(37)
sage: E = EllipticCurve('37a'); phi = E.modular_parametrization()
sage: phi(x)
Heegner point of discriminant -7 on elliptic curve of conductor 37
Draw a point at 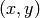 where this Heegner point is
represented by the point
where this Heegner point is
represented by the point 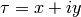 in the upper half
plane.
in the upper half
plane.
The kwds get passed onto the point plotting command.
EXAMPLES:
sage: heegner_point(389,-7,1).plot(pointsize=50)
Return the integral primitive positive-definite binary quadratic form associated to this Heegner point.
EXAMPLES:
sage: heegner_point(389,-7,5).quadratic_form()
389*x^2 + 147*x*y + 14*y^2
Return reduced binary quadratic corresponding to this Heegner point.
EXAMPLES:
sage: x = heegner_point(389,-7,5)
sage: x.quadratic_form()
389*x^2 + 147*x*y + 14*y^2
sage: x.reduced_quadratic_form()
4*x^2 - x*y + 11*y^2
Return an element tau in the upper half plane that corresponds to this particular Heegner point (actually, tau is in the quadratic imagqinary field K associated to this Heegner point).
EXAMPLES:
sage: x = heegner_point(37,-7,5); tau = x.tau(); tau
5/74*sqrt_minus_7 - 11/74
sage: 37 * tau.minpoly()
37*x^2 + 11*x + 2
sage: x.quadratic_form()
37*x^2 + 11*x*y + 2*y^2
Bases: sage.structure.sage_object.SageObject
The set of Heegner points with given parameters.
EXAMPLES:
sage: H = heegner_points(389); H
Set of all Heegner points on X_0(389)
sage: type(H)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerPoints_level'>
sage: isinstance(H, sage.schemes.elliptic_curves.heegner.HeegnerPoints)
True
Return the level  of the modular curve
of the modular curve 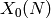 .
.
EXAMPLES:
sage: heegner_points(389).level()
389
Bases: sage.schemes.elliptic_curves.heegner.HeegnerPoints
Return the infinite set of all Heegner points on 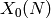 for all
quadratic imaginary fields.
for all
quadratic imaginary fields.
EXAMPLES:
sage: H = heegner_points(11); H
Set of all Heegner points on X_0(11)
sage: type(H)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerPoints_level'>
sage: loads(dumps(H)) == H
True
Return the first  quadratic imaginary discriminants that
satisfy the Heegner hypothesis for
quadratic imaginary discriminants that
satisfy the Heegner hypothesis for  .
.
INPUTS:
– nonnegative integer
- weak – bool (default: False); if True only require weak Heegner hypothesis, which is the same as usual but without the condition that
.
EXAMPLES:
sage: X = heegner_points(37)
sage: X.discriminants(5)
[-7, -11, -40, -47, -67]
The default is 10:
sage: X.discriminants()
[-7, -11, -40, -47, -67, -71, -83, -84, -95, -104]
sage: X.discriminants(15)
[-7, -11, -40, -47, -67, -71, -83, -84, -95, -104, -107, -115, -120, -123, -127]
The discriminant -111 satisfies only the weak Heegner hypothesis, since it is divisible by 37:
sage: X.discriminants(15,weak=True)
[-7, -11, -40, -47, -67, -71, -83, -84, -95, -104, -107, -111, -115, -120, -123]
eturn object that allows for computation with Heegner points
of level  modulo the prime
modulo the prime 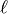 , represented using
quaternion algebras.
, represented using
quaternion algebras.
INPUT:
– prime
EXAMPLES:
sage: heegner_points(389).reduce_mod(7).quaternion_algebra()
Quaternion Algebra (-1, -7) with base ring Rational Field
Bases: sage.schemes.elliptic_curves.heegner.HeegnerPoints
Set of Heegner points of given level and all conductors associated to a quadratic imaginary field.
EXAMPLES:
sage: H = heegner_points(389,-7); H
Set of all Heegner points on X_0(389) associated to QQ[sqrt(-7)]
sage: type(H)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerPoints_level_disc'>
sage: H._repr_()
'Set of all Heegner points on X_0(389) associated to QQ[sqrt(-7)]'
sage: H.discriminant()
-7
sage: H.quadratic_field()
Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
sage: H.kolyvagin_conductors()
[1, 3, 5, 13, 15, 17, 19, 31, 39, 41]
sage: loads(dumps(H)) == H
True
Return the discriminant of the quadratic imaginary extension  .
.
EXAMPLES:
sage: heegner_points(389,-7).discriminant()
-7
Return the first  conductors that are squarefree products
of distinct primes inert in the quadratic imaginary field
conductors that are squarefree products
of distinct primes inert in the quadratic imaginary field
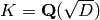 . If
. If  is specified, return only
conductors that are a product of
is specified, return only
conductors that are a product of  distinct primes all inert
in
distinct primes all inert
in  . If
. If 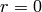 , always return the list [1],
no matter what.
, always return the list [1],
no matter what.
If the optional elliptic curve  and integer
and integer 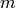 are given,
then only include conductors
are given,
then only include conductors  such that for each prime
divisor
such that for each prime
divisor  of
of  we have
we have 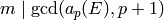 .
.
INPUT:
– (default: None) nonnegative integer or None
– positive integer
– an elliptic curve
– a positive integer
EXAMPLES:
sage: H = heegner_points(389,-7)
sage: H.kolyvagin_conductors(0)
[1]
sage: H.kolyvagin_conductors(1)
[3, 5, 13, 17, 19, 31, 41, 47, 59, 61]
sage: H.kolyvagin_conductors(1,15)
[3, 5, 13, 17, 19, 31, 41, 47, 59, 61, 73, 83, 89, 97, 101]
sage: H.kolyvagin_conductors(1,5)
[3, 5, 13, 17, 19]
sage: H.kolyvagin_conductors(1,5,EllipticCurve('389a'),3)
[5, 17, 41, 59, 83]
sage: H.kolyvagin_conductors(2,5,EllipticCurve('389a'),3)
[85, 205, 295, 415, 697]
Return the quadratic imaginary field 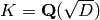 .
.
EXAMPLES:
sage: E = EllipticCurve('389a'); K = E.heegner_point(-7,5).ring_class_field()
sage: K.quadratic_field()
Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
Bases: sage.schemes.elliptic_curves.heegner.HeegnerPoints_level, sage.schemes.elliptic_curves.heegner.HeegnerPoints_level_disc
The set of Heegner points of given level, discriminant, and conductor.
EXAMPLES:
sage: H = heegner_points(389,-7,5); H
All Heegner points of conductor 5 on X_0(389) associated to QQ[sqrt(-7)]
sage: type(H)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerPoints_level_disc_cond'>
sage: H.discriminant()
-7
sage: H.level()
389
sage: len(H.points())
12
sage: H.points()[0]
Heegner point 5/778*sqrt(-7) - 147/778 of discriminant -7 and conductor 5 on X_0(389)
sage: H.betas()
(147, 631)
sage: H.quadratic_field()
Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
sage: H.ring_class_field()
Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: H.kolyvagin_conductors()
[1, 3, 5, 13, 15, 17, 19, 31, 39, 41]
sage: H.satisfies_kolyvagin_hypothesis()
True
sage: H = heegner_points(389,-7,5)
sage: loads(dumps(H)) == H
True
Return the square roots of 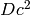 modulo
modulo 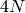 all reduced
mod
all reduced
mod 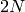 , without multiplicity.
, without multiplicity.
EXAMPLES:
sage: X = heegner_points(45,-11,1); X
All Heegner points of conductor 1 on X_0(45) associated to QQ[sqrt(-11)]
sage: [x.quadratic_form() for x in X]
[45*x^2 + 13*x*y + y^2,
45*x^2 + 23*x*y + 3*y^2,
45*x^2 + 67*x*y + 25*y^2,
45*x^2 + 77*x*y + 33*y^2]
sage: X.betas()
(13, 23, 67, 77)
sage: X.points(13)
(Heegner point 1/90*sqrt(-11) - 13/90 of discriminant -11 on X_0(45),)
sage: [x.quadratic_form() for x in X.points(13)]
[45*x^2 + 13*x*y + y^2]
Return the level of the conductor.
EXAMPLES:
sage: heegner_points(389,-7,5).conductor()
5
Returns plot of all the representatives in the upper half plane of the Heegner points in this set of Heegner points.
The inputs to this function get passed onto the point command.
EXAMPLES:
sage: heegner_points(389,-7,5).plot(pointsize=50, rgbcolor='red')
sage: heegner_points(53,-7,15).plot(pointsize=50, rgbcolor='purple')
Return the Heegner points in self. If  is given,
return only those Heegner points with given
is given,
return only those Heegner points with given  , i.e.,
whose quadratic form has
, i.e.,
whose quadratic form has 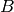 congruent to
congruent to  modulo
modulo 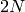 .
.
Use self.beta() to get a list of betas.
EXAMPLES:
sage: H = heegner_points(389,-7,5); H
All Heegner points of conductor 5 on X_0(389) associated to QQ[sqrt(-7)]
sage: H.points()
(Heegner point 5/778*sqrt(-7) - 147/778 of discriminant -7 and conductor 5 on X_0(389), ..., Heegner point 5/5446*sqrt(-7) - 757/778 of discriminant -7 and conductor 5 on X_0(389))
sage: H.betas()
(147, 631)
sage: [x.tau() for x in H.points(147)]
[5/778*sqrt_minus_7 - 147/778, 5/1556*sqrt_minus_7 - 147/1556, 5/1556*sqrt_minus_7 - 925/1556, 5/3112*sqrt_minus_7 - 1703/3112, 5/3112*sqrt_minus_7 - 2481/3112, 5/5446*sqrt_minus_7 - 21/778]
sage: [x.tau() for x in H.points(631)]
[5/778*sqrt_minus_7 - 631/778, 5/1556*sqrt_minus_7 - 631/1556, 5/1556*sqrt_minus_7 - 1409/1556, 5/3112*sqrt_minus_7 - 631/3112, 5/3112*sqrt_minus_7 - 1409/3112, 5/5446*sqrt_minus_7 - 757/778]
The result is cached and is a tuple (since it is immutable):
sage: H.points() is H.points()
True
sage: type(H.points())
<type 'tuple'>
Return the ring class field associated to this set of Heegner
points. This is an extension  over
over  , where
, where  is the
quadratic imaginary field and
is the
quadratic imaginary field and  the conductor associated to
this Heegner point. This Heegner point is defined over
the conductor associated to
this Heegner point. This Heegner point is defined over  and the Galois group
and the Galois group 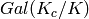 acts transitively on the
Galois conjugates of this Heegner point.
acts transitively on the
Galois conjugates of this Heegner point.
EXAMPLES:
sage: heegner_points(389,-7,5).ring_class_field()
Ring class field extension of QQ[sqrt(-7)] of conductor 5
Return True if self satisfies the Kolyvagin hypothesis, i.e.,
that each prime dividing the conductor  of self is inert in
of self is inert in
 and coprime to
and coprime to 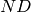 .
.
EXAMPLES:
The prime 5 is inert, but the prime 11 isn’t:
sage: heegner_points(389,-7,5).satisfies_kolyvagin_hypothesis()
True
sage: heegner_points(389,-7,11).satisfies_kolyvagin_hypothesis()
False
Bases: sage.structure.sage_object.SageObject
Heegner points viewed as supersingular points on the modular curve
 .
.
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(13); H
Heegner points on X_0(11) over F_13
sage: type(H)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerQuatAlg'>
sage: loads(dumps(H)) == H
True
Return the Brandt module of right ideal classes that we used to represent the set of supersingular points on the modular curve.
EXAMPLES:
sage: heegner_points(11).reduce_mod(3).brandt_module()
Brandt module of dimension 2 of level 3*11 of weight 2 over Rational Field
Compute dictionary mapping 2-tuples that defined normalized
elements of 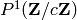
INPUT:
– right ideal of Eichler order or in quaternion algebra
– square free integer (currently must be odd prime
and coprime to level, discriminant, characteristic, etc.
OUTPUT:
- dictionary mapping 2-tuples (u,v) to ideals
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(7)
sage: I = H.brandt_module().right_ideals()[0]
sage: sorted(H.cyclic_subideal_p1(I,3).iteritems())
[((0, 1),
Fractional ideal (2 + 2*j + 32*k, 2*i + 8*j + 82*k, 12*j + 60*k, 132*k)),
((1, 0),
Fractional ideal (2 + 10*j + 28*k, 2*i + 4*j + 62*k, 12*j + 60*k, 132*k)),
((1, 1),
Fractional ideal (2 + 2*j + 76*k, 2*i + 4*j + 106*k, 12*j + 60*k, 132*k)),
((1, 2),
Fractional ideal (2 + 10*j + 116*k, 2*i + 8*j + 38*k, 12*j + 60*k, 132*k))]
sage: len(H.cyclic_subideal_p1(I,17))
18
Return the prime 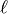 modulo which we are working.
modulo which we are working.
EXAMPLES:
sage: heegner_points(11).reduce_mod(3).ell()
3
Return the Galois group of the extension of ring class fields
 over the Hilbert class field
over the Hilbert class field  of the quadratic
imaginary field of discriminant
of the quadratic
imaginary field of discriminant  .
.
INPUT:
– fundamental discriminant
– conductor (square-free integer)
EXAMPLES:
sage: N = 37; D = -7; ell = 17; c = 41; p = 3
sage: H = heegner_points(N).reduce_mod(ell)
sage: H.galois_group_over_hilbert_class_field(D, c)
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 41 over Hilbert class field of QQ[sqrt(-7)]
Return the Galois group of the extension of ring class fields
 over the quadratic imaginary field
over the quadratic imaginary field  of discriminant
of discriminant  .
.
INPUT:
– fundamental discriminant
– conductor (square-free integer)
EXAMPLES:
sage: N = 37; D = -7; ell = 17; c = 41; p = 3
sage: H = heegner_points(N).reduce_mod(ell)
sage: H.galois_group_over_quadratic_field(D, c)
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 41 over Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
Return the first  negative fundamental discriminants
coprime to
negative fundamental discriminants
coprime to 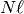 such that
such that 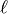 is inert in the
corresponding quadratic imaginary field and that field
satisfies the Heegner hypothesis.
is inert in the
corresponding quadratic imaginary field and that field
satisfies the Heegner hypothesis.
INPUT:
– negative integer; a fundamental Heegner discriminant
– positive integer (default: 5)
OUTPUT:
- list
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3)
sage: H.heegner_conductors(-7)
[1, 2, 4, 5, 8]
sage: H.heegner_conductors(-7, 10)
[1, 2, 4, 5, 8, 10, 13, 16, 17, 19]
Return the first  negative fundamental discriminants
coprime to
negative fundamental discriminants
coprime to 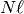 such that
such that 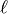 is inert in the
corresponding quadratic imaginary field and that field
satisfies the Heegner hypothesis, and
is inert in the
corresponding quadratic imaginary field and that field
satisfies the Heegner hypothesis, and  is the level.
is the level.
INPUT:
– positive integer (default: 5)
OUTPUT:
- list
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3)
sage: H.heegner_discriminants()
[-7, -19, -40, -43, -52]
sage: H.heegner_discriminants(10)
[-7, -19, -40, -43, -52, -79, -127, -139, -151, -184]
Return Heegner divisor as an element of the Brandt module
corresponding to the discriminant  and conductor
and conductor  , which
both must be coprime to
, which
both must be coprime to 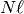 .
.
More precisely, we compute the sum of the reductions of the
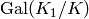 -conjugates of each choice of
-conjugates of each choice of 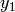 ,
where the choice comes from choosing the ideal
,
where the choice comes from choosing the ideal 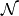 .
Then we apply the Hecke operator
.
Then we apply the Hecke operator 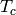 to this sum.
to this sum.
INPUT:
– discriminant (negative integer)
– conductor (positive integer)
OUTPUT:
- Brandt module element
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(7)
sage: H.heegner_discriminants()
[-8, -39, -43, -51, -79]
sage: H.heegner_divisor(-8)
(1, 0, 0, 1, 0, 0)
sage: H.heegner_divisor(-39)
(1, 2, 2, 1, 2, 0)
sage: H.heegner_divisor(-43)
(1, 0, 0, 1, 0, 0)
sage: H.heegner_divisor(-51)
(1, 0, 0, 1, 0, 2)
sage: H.heegner_divisor(-79)
(3, 2, 2, 3, 0, 0)
sage: sum(H.heegner_divisor(-39).element())
8
sage: QuadraticField(-39,'a').class_number()
4
Return list of pairs 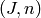 where
where 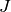 runs through the
cyclic subideals of
runs through the
cyclic subideals of  of index
of index  , and
, and  for some fixed choice of cyclic subideal
for some fixed choice of cyclic subideal  .
.
INPUT:
– right ideal of the quaternion algebra
– prime number
- alpha_quaternion – image in the quaternion algebra
of generator
for
.
OUTPUT:
- list of 2-tuples
EXAMPLES:
sage: N = 37; D = -7; ell = 17; c=5
sage: H = heegner_points(N).reduce_mod(ell)
sage: B = H.brandt_module(); I = B.right_ideals()[32]
sage: f = H.optimal_embeddings(D, 1, I.left_order())[0]
sage: g = H.kolyvagin_generators(f.domain().number_field(), c)
sage: alpha_quaternion = f(g[0]); alpha_quaternion
1 - 5/128*i - 77/192*j + 137/384*k
sage: H.kolyvagin_cyclic_subideals(I, 5, alpha_quaternion)
[(Fractional ideal (2 + 874/3*j + 128356/3*k, 2*i + 932/3*j + 198806/3*k, 2560/3*j + 33280/3*k, 94720*k), 0), (Fractional ideal (2 + 462*j + 82892*k, 2*i + 932/3*j + 141974/3*k, 2560/3*j + 33280/3*k, 94720*k), 1), (Fractional ideal (2 + 2410/3*j + 261988/3*k, 2*i + 652*j + 89650*k, 2560/3*j + 33280/3*k, 94720*k), 2), (Fractional ideal (2 + 2410/3*j + 91492/3*k, 2*i + 1444/3*j + 148630/3*k, 2560/3*j + 33280/3*k, 94720*k), 3), (Fractional ideal (2 + 874/3*j + 71524/3*k, 2*i + 2468/3*j + 275606/3*k, 2560/3*j + 33280/3*k, 94720*k), 4), (Fractional ideal (2 + 462*j + 63948*k, 2*i + 2468/3*j + 218774/3*k, 2560/3*j + 33280/3*k, 94720*k), 5)]
Return element in  that maps to the multiplicative generator
for the quotient group
that maps to the multiplicative generator
for the quotient group
of the form  with
with  minimal.
minimal.
INPUT:
– quadratic imaginary field
– inert prime
EXAMPLES:
sage: N = 37; D = -7; ell = 17; p=5
sage: H = heegner_points(N).reduce_mod(ell)
sage: B = H.brandt_module(); I = B.right_ideals()[32]
sage: f = H.optimal_embeddings(D, 1, I.left_order())[0]
sage: H.kolyvagin_generator(f.domain().number_field(), 5)
a + 1
This function requires that p be prime, but kolyvagin_generators works in general:
sage: H.kolyvagin_generator(f.domain().number_field(), 5*17)
...
NotImplementedError: p must be prime
sage: H.kolyvagin_generators(f.domain().number_field(), 5*17)
[-34*a + 1, 35*a + 106]
Return elements in 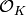 that map to multiplicative generators
for the factors of the quotient group
that map to multiplicative generators
for the factors of the quotient group
corresponding to the prime divisors of c. Each generator is
of the form 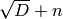 with
with  minimal.
minimal.
INPUT:
– quadratic imaginary field
– square free product of inert prime
EXAMPLES:
sage: N = 37; D = -7; ell = 17; p=5
sage: H = heegner_points(N).reduce_mod(ell)
sage: B = H.brandt_module(); I = B.right_ideals()[32]
sage: f = H.optimal_embeddings(D, 1, I.left_order())[0]
sage: H.kolyvagin_generators(f.domain().number_field(), 5*17)
[-34*a + 1, 35*a + 106]
Compute image of the Kolyvagin divisor 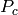 in
in
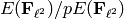 . Note that
this image is by definition only well defined up to
scalars. However, doing multiple computations
will always yield the same result, and working
modulo different
. Note that
this image is by definition only well defined up to
scalars. However, doing multiple computations
will always yield the same result, and working
modulo different 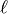 is compatible (since we
always chose the same generator for
is compatible (since we
always chose the same generator for 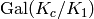 ).
).
INPUT:
– fundamental negative discriminant
– conductor
– elliptic curve of conductor the level of self
– odd prime number such that we consider image in
bound – integer (default: 10)
EXAMPLES:
sage: N = 37; D = -7; ell = 17; c = 41; p = 3
sage: H = heegner_points(N).reduce_mod(ell)
sage: H.kolyvagin_point_on_curve(D, c, EllipticCurve('37a'), p)
[1, 1]
Return the action of the Kolyvagin sigma operator on the  -th
basis vector.
-th
basis vector.
INPUT:
– fundamental discriminant
– conductor (square-free integer, need not be prime)
– nonnegative integer
- bound – (default: None), if given, controls precision of computation of theta series, which could impact performance, but does not impact correctness
EXAMPLES:
We first try to verify Kolyvagin’s conjecture for a rank 2
curve by working modulo 5, but we are unlucky with 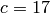 :
:
sage: N = 389; D = -7; ell = 5; c = 17; q = 3
sage: H = heegner_points(N).reduce_mod(ell)
sage: V = H.modp_dual_elliptic_curve_factor(EllipticCurve('389a'), q, 5)
sage: k118 = H.kolyvagin_sigma_operator(D, c, 118)
sage: k104 = H.kolyvagin_sigma_operator(D, c, 104)
sage: [b.dot_product(k104.element().change_ring(GF(3))) for b in V.basis()]
[0, 0]
sage: [b.dot_product(k118.element().change_ring(GF(3))) for b in V.basis()]
[0, 0]
Next we try again with 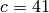 and this does work, in that we
get something nonzero, when dotting with V:
and this does work, in that we
get something nonzero, when dotting with V:
sage: c = 41
sage: k118 = H.kolyvagin_sigma_operator(D, c, 118)
sage: k104 = H.kolyvagin_sigma_operator(D, c, 104)
sage: [b.dot_product(k118.element().change_ring(GF(3))) for b in V.basis()]
[1, 0]
sage: [b.dot_product(k104.element().change_ring(GF(3))) for b in V.basis()]
[1, 0]
By the way, the above is the first ever provable verification of Kolyvagin’s conjecture for any curve of rank at least 2.
Another example, but where the curve has rank 1:
sage: N = 37; D = -7; ell = 17; c = 41; q = 3
sage: H = heegner_points(N).reduce_mod(ell)
sage: H.heegner_divisor(D,1).element().nonzero_positions()
[32, 51]
sage: k32 = H.kolyvagin_sigma_operator(D, c, 32); k32
(63, 68, 47, 47, 31, 52, 37, 0, 0, 47, 3, 31, 47, 7, 21, 26, 19, 10, 0, 0, 11, 28, 41, 2, 47, 25, 0, 0, 36, 0, 33, 0, 0, 0, 40, 6, 14, 22, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
sage: k51 = H.kolyvagin_sigma_operator(D, c, 51); k51
(5, 13, 0, 0, 14, 0, 21, 0, 0, 0, 29, 0, 0, 45, 0, 6, 0, 40, 0, 61, 0, 0, 40, 32, 0, 9, 0, 0, 0, 0, 17, 0, 0, 0, 77, 40, 2, 10, 18, 0, 0, 61, 19, 45, 26, 80, 61, 35, 35, 19, 1, 0)
sage: V = H.modp_dual_elliptic_curve_factor(EllipticCurve('37a'), q, 5); V
Vector space of degree 52 and dimension 2 over Ring of integers modulo 3
Basis matrix:
2 x 52 dense matrix over Ring of integers modulo 3
sage: [b.dot_product(k32.element().change_ring(GF(q))) for b in V.basis()]
[1, 1]
sage: [b.dot_product(k51.element().change_ring(GF(q))) for b in V.basis()]
[1, 1]
An example with  a product of two primes:
a product of two primes:
sage: N = 389; D = -7; ell = 5; q = 3
sage: H = heegner_points(N).reduce_mod(ell)
sage: V = H.modp_dual_elliptic_curve_factor(EllipticCurve('389a'), q, 5)
sage: k = H.kolyvagin_sigma_operator(D, 17*41, 104) # long time
sage: k # long time
(990, 656, 219, ..., 246, 534, 1254)
sage: [b.dot_product(k.element().change_ring(GF(3))) for b in V.basis()] # long time (but only because depends on something slow)
[0, 0]
Return the left orders associated to the representative right ideals in the Brandt module.
EXAMPLES:
sage: heegner_points(11).reduce_mod(3).left_orders()
[Order of Quaternion Algebra (-1, -3) with base ring Rational Field with basis (1/2 + 1/2*j + 7*k, 1/2*i + 13/2*k, j + 3*k, 11*k),
Order of Quaternion Algebra (-1, -3) with base ring Rational Field with basis (1/2 + 1/2*j + 7*k, 1/4*i + 1/2*j + 63/4*k, j + 14*k, 22*k)]
Return the level.
EXAMPLES:
sage: heegner_points(11).reduce_mod(3).level()
11
Return the factor of the Brandt module space modulo  corresponding to the elliptic curve
corresponding to the elliptic curve  , cut out using
Hecke operators up to bound.
, cut out using
Hecke operators up to bound.
INPUT:
– elliptic curve of conductor equal to the level of self
– prime number
– positive integer (default: 10)
EXAMPLES:
sage: N = 37; D = -7; ell = 17; c = 41; q = 3
sage: H = heegner_points(N).reduce_mod(ell)
sage: V = H.modp_dual_elliptic_curve_factor(EllipticCurve('37a'), q, 5); V
Vector space of degree 52 and dimension 2 over Ring of integers modulo 3
Basis matrix:
2 x 52 dense matrix over Ring of integers modulo 3
Return mod  splitting data for the quaternion algebra at the
unramified prime
splitting data for the quaternion algebra at the
unramified prime  . This is a pair of
. This is a pair of  matrices
matrices
 ,
, 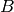 over the finite field
over the finite field 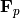 such that if the
quaternion algebra has generators
such that if the
quaternion algebra has generators 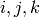 , then the
homomorphism sending
, then the
homomorphism sending  to
to  and
and 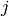 to
to 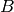 maps any
maximal order homomorphically onto the ring of
maps any
maximal order homomorphically onto the ring of  matrices.
matrices.
Because of how the homomorphism is defined, we must assume that the
prime  is odd.
is odd.
INPUT:
– unramified odd prime
OUTPUT:
- 2-tuple of matrices over finite field
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(7)
sage: H.quaternion_algebra()
Quaternion Algebra (-1, -7) with base ring Rational Field
sage: I, J = H.modp_splitting_data(13)
sage: I
[ 0 12]
[ 1 0]
sage: J
[7 3]
[3 6]
sage: I^2
[12 0]
[ 0 12]
sage: J^2
[6 0]
[0 6]
sage: I*J == -J*I
True
The following is a good test because of the asserts in the code:
sage: v = [H.modp_splitting_data(p) for p in primes(13,200)]
Some edge cases:
sage: H.modp_splitting_data(11)
(
[ 0 10] [6 1]
[ 1 0], [1 5]
)
Proper error handling:
sage: H.modp_splitting_data(7)
...
ValueError: p (=7) must be an unramified prime
sage: H.modp_splitting_data(2)
...
ValueError: p must be odd
Return (algebra) map from the ( -integral) quaternion algebra to
the set of
-integral) quaternion algebra to
the set of  matrices over
matrices over 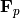 .
.
INPUT:
– prime number
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(7)
sage: f = H.modp_splitting_map(13)
sage: B = H.quaternion_algebra(); B
Quaternion Algebra (-1, -7) with base ring Rational Field
sage: i,j,k = H.quaternion_algebra().gens()
sage: a = 2+i-j+3*k; b = 7+2*i-4*j+k
sage: f(a*b)
[12 3]
[10 5]
sage: f(a)*f(b)
[12 3]
[10 5]
INPUT:
– negative fundamental disriminant
– integer coprime
– Eichler order
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3)
sage: R = H.left_orders()[0]
sage: H.optimal_embeddings(-7, 1, R)
[Embedding sending sqrt(-7) to -i + j + k,
Embedding sending sqrt(-7) to i - j - k]
sage: H.optimal_embeddings(-7, 2, R)
[Embedding sending 2*sqrt(-7) to -5*i + k,
Embedding sending 2*sqrt(-7) to 5*i - k,
Embedding sending 2*sqrt(-7) to -2*i + 2*j + 2*k,
Embedding sending 2*sqrt(-7) to 2*i - 2*j - 2*k]
Return our fixed choice of quadratic imaginary field of
discriminant  .
.
INPUT:
– fundamental discriminant
OUTPUT:
- a quadratic number field
EXAMPLES:
sage: H = heegner_points(389).reduce_mod(5)
sage: H.quadratic_field(-7)
Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
Return the rational quaternion algebra used to implement self.
EXAMPLES:
sage: heegner_points(389).reduce_mod(7).quaternion_algebra()
Quaternion Algebra (-1, -7) with base ring Rational Field
Return the Kolyvagin divisor as an element of the Brandt module
corresponding to the discriminant  and conductor
and conductor  , which
both must be coprime to
, which
both must be coprime to 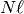 .
.
INPUT:
– discriminant (negative integer)
– conductor (positive integer)
OUTPUT:
- Brandt module element (or tuple of them)
EXAMPLES:
sage: N = 389; D = -7; ell = 5; c = 17; q = 3
sage: H = heegner_points(N).reduce_mod(ell)
sage: k = H.rational_kolyvagin_divisor(D, c); k
(2, 0, 0, 0, 0, 0, 16, 0, 0, 0, 0, 4, 0, 0, 9, 11, 0, 6, 0, 0, 7, 0, 0, 0, 0, 14, 12, 13, 15, 17, 0, 0, 0, 0, 8, 0, 0, 0, 0, 10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
sage: V = H.modp_dual_elliptic_curve_factor(EllipticCurve('389a'), q, 2)
sage: [b.dot_product(k.element().change_ring(GF(q))) for b in V.basis()]
[0, 0]
sage: k = H.rational_kolyvagin_divisor(D, 59)
sage: [b.dot_product(k.element().change_ring(GF(q))) for b in V.basis()]
[2, 0]
Return representative right ideals in the Brandt module.
EXAMPLES:
sage: heegner_points(11).reduce_mod(3).right_ideals()
(Fractional ideal (2 + 2*j + 28*k, 2*i + 26*k, 4*j + 12*k, 44*k),
Fractional ideal (2 + 2*j + 28*k, 2*i + 4*j + 38*k, 8*j + 24*k, 88*k))
The fundamental discriminant  must be coprime to
must be coprime to 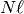 ,
and must define a quadratic imaginary field
,
and must define a quadratic imaginary field  in which
in which 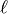 is inert. Also, all primes dividing
is inert. Also, all primes dividing  must split in
must split in  ,
and
,
and  must be squarefree and coprime to
must be squarefree and coprime to 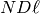 .
.
INPUT:
– negative integer
– positive integer (default: 1)
OUTPUT:
- bool
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(7)
sage: H.satisfies_heegner_hypothesis(-5)
False
sage: H.satisfies_heegner_hypothesis(-7)
False
sage: H.satisfies_heegner_hypothesis(-8)
True
sage: [D for D in [-1,-2..-100] if H.satisfies_heegner_hypothesis(D)]
[-8, -39, -43, -51, -79, -95]
Bases: sage.structure.sage_object.SageObject
The homomorphism 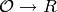 , where
, where 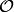 is the
order of conductor
is the
order of conductor  in the quadratic field of discriminant
in the quadratic field of discriminant  ,
and
,
and 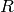 is an Eichler order in a quaternion algebra.
is an Eichler order in a quaternion algebra.
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3); R = H.left_orders()[0]
sage: f = H.optimal_embeddings(-7, 2, R)[0]; f
Embedding sending 2*sqrt(-7) to -5*i + k
sage: type(f)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerQuatAlgEmbedding'>
sage: loads(dumps(f)) == f
True
Return the element  in the quaternion algebra order
that
in the quaternion algebra order
that 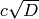 maps to.
maps to.
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3); R = H.left_orders()[0]
sage: H.optimal_embeddings(-7, 2, R)[0].beta()
-5*i + k
Return the codomain of this embedding.
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3); R = H.left_orders()[0]
sage: H.optimal_embeddings(-7, 2, R)[0].codomain()
Order of Quaternion Algebra (-1, -3) with base ring Rational Field with basis (1/2 + 1/2*j + 7*k, 1/2*i + 13/2*k, j + 3*k, 11*k)
Return the conjugate of this embedding, which is also an embedding.
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3); R = H.left_orders()[0]
sage: f = H.optimal_embeddings(-7, 2, R)[0]
sage: f.conjugate()
Embedding sending 2*sqrt(-7) to 5*i - k
sage: f
Embedding sending 2*sqrt(-7) to -5*i + k
Return the domain of this embedding.
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3); R = H.left_orders()[0]
sage: H.optimal_embeddings(-7, 2, R)[0].domain()
Order in Number Field in a with defining polynomial x^2 + 7
Return the conductor of the domain.
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3); R = H.left_orders()[0]
sage: H.optimal_embeddings(-7, 2, R)[0].domain_conductor()
2
Return the specific generator 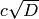 for the domain
order.
for the domain
order.
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3); R = H.left_orders()[0]
sage: f = H.optimal_embeddings(-7, 2, R)[0]
sage: f.domain_gen()
2*a
sage: f.domain_gen()^2
-28
Return matrix over  of this morphism, with respect to the
basis 1,
of this morphism, with respect to the
basis 1, 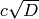 of the domain and the basis
of the domain and the basis 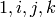 of
the ambient rational quaternion algebra (which contains the
domain).
of
the ambient rational quaternion algebra (which contains the
domain).
EXAMPLES:
sage: H = heegner_points(11).reduce_mod(3); R = H.left_orders()[0]
sage: f = H.optimal_embeddings(-7, 1, R)[0]; f
Embedding sending sqrt(-7) to -i + j + k
sage: f.matrix()
[ 1 0 0 0]
[ 0 -1 1 1]
sage: f.conjugate().matrix()
[ 1 0 0 0]
[ 0 1 -1 -1]
Bases: sage.structure.sage_object.SageObject
A Kolyvagin cohomology class in ![H^1(K,E[n])](../../../_images/math/9b6b97aaf88b9aa1af24cf820fb825728dcbcb77.png) or
or ![H^1(K,E)[n]](../../../_images/math/67af596547aa0ea058e56108b9f83a39f6c12560.png) attached to a Heegner point.
attached to a Heegner point.
EXAMPLES:
sage: y = EllipticCurve('37a').heegner_point(-7)
sage: c = y.kolyvagin_cohomology_class(3); c
Kolyvagin cohomology class c(1) in H^1(K,E[3])
sage: type(c)
<class 'sage.schemes.elliptic_curves.heegner.KolyvaginCohomologyClassEn'>
sage: loads(dumps(c)) == c
True
sage: y.kolyvagin_cohomology_class(5)
Kolyvagin cohomology class c(1) in H^1(K,E[5])
Return the integer  such that this cohomology class is associated
to the Heegner point
such that this cohomology class is associated
to the Heegner point 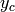 .
.
EXAMPLES:
sage: y = EllipticCurve('37a').heegner_point(-7,5)
sage: t = y.kolyvagin_cohomology_class()
sage: t.conductor()
5
Return the Heegner point 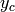 to which this cohomology class
is associated.
to which this cohomology class
is associated.
EXAMPLES:
sage: y = EllipticCurve('37a').heegner_point(-7,5)
sage: t = y.kolyvagin_cohomology_class()
sage: t.heegner_point()
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 37
Return the Kolyvagin point 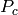 to which this cohomology
class is associated.
to which this cohomology
class is associated.
EXAMPLES:
sage: y = EllipticCurve('37a').heegner_point(-7,5)
sage: t = y.kolyvagin_cohomology_class()
sage: t.kolyvagin_point()
Kolyvagin point of discriminant -7 and conductor 5 on elliptic curve of conductor 37
Return the integer  so that this is a cohomology class in
so that this is a cohomology class in
![H^1(K,E[n])](../../../_images/math/9b6b97aaf88b9aa1af24cf820fb825728dcbcb77.png) or
or ![H^1(K,E)[n]](../../../_images/math/67af596547aa0ea058e56108b9f83a39f6c12560.png) .
.
EXAMPLES:
sage: y = EllipticCurve('37a').heegner_point(-7)
sage: t = y.kolyvagin_cohomology_class(3); t
Kolyvagin cohomology class c(1) in H^1(K,E[3])
sage: t.n()
3
Bases: sage.schemes.elliptic_curves.heegner.KolyvaginCohomologyClass
EXAMPLES:
Bases: sage.schemes.elliptic_curves.heegner.HeegnerPoint
A Kolyvagin point.
EXAMPLES:
We create a few Kolyvagin points:
sage: EllipticCurve('11a1').kolyvagin_point(-7)
Kolyvagin point of discriminant -7 on elliptic curve of conductor 11
sage: EllipticCurve('37a1').kolyvagin_point(-7)
Kolyvagin point of discriminant -7 on elliptic curve of conductor 37
sage: EllipticCurve('37a1').kolyvagin_point(-67)
Kolyvagin point of discriminant -67 on elliptic curve of conductor 37
sage: EllipticCurve('389a1').kolyvagin_point(-7, 5)
Kolyvagin point of discriminant -7 and conductor 5 on elliptic curve of conductor 389
One can also associated a Kolyvagin point to a Heegner point:
sage: y = EllipticCurve('37a1').heegner_point(-7); y
Heegner point of discriminant -7 on elliptic curve of conductor 37
sage: y.kolyvagin_point()
Kolyvagin point of discriminant -7 on elliptic curve of conductor 37
TESTS:
sage: y = EllipticCurve('37a1').heegner_point(-7)
sage: type(y)
<class 'sage.schemes.elliptic_curves.heegner.HeegnerPointOnEllipticCurve'>
sage: loads(dumps(y)) == y
True
Return the elliptic curve over  on which this Kolyvagin
point sits.
on which this Kolyvagin
point sits.
EXAMPLES:
sage: E = EllipticCurve('37a1'); P = E.kolyvagin_point(-67, 3)
sage: P.curve()
Elliptic Curve defined by y^2 + y = x^3 - x over Rational Field
This Kolyvagin point 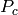 is associated to some Heegner point
is associated to some Heegner point
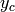 via Kolyvagin’s construction. This function returns that
point
via Kolyvagin’s construction. This function returns that
point 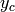 .
.
EXAMPLES:
sage: E = EllipticCurve('37a1')
sage: P = E.kolyvagin_point(-67); P
Kolyvagin point of discriminant -67 on elliptic curve of conductor 37
sage: y = P.heegner_point(); y
Heegner point of discriminant -67 on elliptic curve of conductor 37
sage: y.kolyvagin_point() is P
True
Return index of this Kolyvagin point in the full group of
 rational points on
rational points on  .
.
When the conductor is 1, this is computed numerically using
the Gross-Zagier formula and explicit point search, and it may
be off by  . See the documentation for E.heegner_index,
where
. See the documentation for E.heegner_index,
where  is the curve attached to self.
is the curve attached to self.
EXAMPLES:
sage: E = EllipticCurve('37a1'); P = E.kolyvagin_point(-67); P.index()
6
INPUT:
– positive integer that divides the gcd of
and
for all
dividing the conductor. If
is None, choose the largest valid
.
EXAMPLES:
sage: y = EllipticCurve('389a').heegner_point(-7,5)
sage: P = y.kolyvagin_point()
sage: P.kolyvagin_cohomology_class(3)
Kolyvagin cohomology class c(5) in H^1(K,E[3])
sage: y = EllipticCurve('37a').heegner_point(-7,5).kolyvagin_point()
sage: y.kolyvagin_cohomology_class()
Kolyvagin cohomology class c(5) in H^1(K,E[2])
Return the trace of the reduction 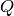 modulo a prime over
modulo a prime over  of this
Kolyvagin point as an element of
of this
Kolyvagin point as an element of 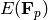 , where
, where
 is any prime that is inert in
is any prime that is inert in  that is coprime to
that is coprime to 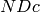 .
The point
.
The point 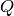 is only well defined up to an element of
is only well defined up to an element of
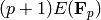 , i.e., it gives a well defined element
of the abelian group
, i.e., it gives a well defined element
of the abelian group 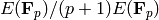 .
.
See Stein, “Toward a Generalization of the Gross-Zagier Conjecture”, Proposition 5.4 for a proof of the above well-definedness assertion.
EXAMPLES:
A Kolyvagin point on a rank 1 curve:
sage: E = EllipticCurve('37a1'); P = E.kolyvagin_point(-67)
sage: P.mod(2)
(1 : 1 : 1)
sage: P.mod(3)
(1 : 0 : 1)
sage: P.mod(5)
(2 : 2 : 1)
sage: P.mod(7)
(6 : 0 : 1)
sage: P.trace_to_real_numerical()
(1.61355529131986 : -2.18446840788880 : 1.00000000000000)
sage: P._trace_exact_conductor_1() # the actual point we're reducing
(1357/841 : -53277/24389 : 1)
sage: (P._trace_exact_conductor_1().height() / E.regulator()).sqrt()
12.0000000000000
Here the Kolyvagin point is a torsion point (since  has
rank 1), and we reduce it modulo several primes.:
has
rank 1), and we reduce it modulo several primes.:
sage: E = EllipticCurve('11a1'); P = E.kolyvagin_point(-7)
sage: P.mod(3,70)
(1 : 2 : 1)
sage: P.mod(5,70)
(1 : 4 : 1)
sage: P.mod(7,70)
...
ValueError: p must be coprime to conductors and discriminant
sage: P.mod(11,70)
...
ValueError: p must be coprime to conductors and discriminant
sage: P.mod(13,70)
(3 : 4 : 1)
Return a numerical approximation to this Kolyvagin point using prec bits of working precision.
INPUT:
- prec – precision in bits (default: 53)
EXAMPLES:
sage: P = EllipticCurve('37a1').kolyvagin_point(-7); P
Kolyvagin point of discriminant -7 on elliptic curve of conductor 37
sage: P.numerical_approx()
(-3.4...e-16 - 2.00...e-16*I : 3.42...e-16 + 2.00...e-16*I : 1.00000000000000)
sage: P.numerical_approx(10)
(0.0030 - 0.0028*I : -0.0030 + 0.0028*I : 1.0)
sage: P.numerical_approx(100)[0]
8.4419827889841225189186778139e-31 + 6.087647...e-31*I
sage: P = EllipticCurve('389a1').kolyvagin_point(-7, 5); P
Kolyvagin point of discriminant -7 and conductor 5 on elliptic curve of conductor 389
Numerical approximation is not yet implemented:
sage: P.numerical_approx()
...
NotImplementedError
Plot a Kolyvagin point  if it is defined over the
rational numbers.
if it is defined over the
rational numbers.
EXAMPLES:
sage: E = EllipticCurve('37a'); P = E.heegner_point(-11).kolyvagin_point()
sage: P.plot(prec=30, pointsize=50, rgbcolor='red') + E.plot()
INPUT:
- prec – precision in bits (default: 53)
EXAMPLES:
A rank 1 curve:
sage: E = EllipticCurve('37a1'); P = E.kolyvagin_point(-67)
sage: P.point_exact()
(6 : -15 : 1)
sage: P.point_exact(40)
(6 : -15 : 1)
sage: P.point_exact(20)
...
RuntimeError: insufficient precision to find exact point
A rank 0 curve:
sage: E = EllipticCurve('11a1'); P = E.kolyvagin_point(-7)
sage: P.point_exact()
(-1/2*sqrt_minus_7 + 1/2 : -2*sqrt_minus_7 - 2 : 1)
A rank 2 curve:
sage: E = EllipticCurve('389a1'); P = E.kolyvagin_point(-7)
sage: P.point_exact()
... # 64-bit
RuntimeError: insufficient precision to find exact point # 64-bit
(0 : 1 : 0) # 32-bit
sage: P.point_exact(100)
(0 : 1 : 0)
Return True if this Kolyvagin point satisfies the Heegner
hypothesis for  , so that it defines a Galois equivariant
element of
, so that it defines a Galois equivariant
element of  .
.
EXAMPLES:
sage: y = EllipticCurve('389a').heegner_point(-7,5); P = y.kolyvagin_point()
sage: P.kolyvagin_cohomology_class(3)
Kolyvagin cohomology class c(5) in H^1(K,E[3])
sage: P.satisfies_kolyvagin_hypothesis(3)
True
sage: P.satisfies_kolyvagin_hypothesis(5)
False
sage: P.satisfies_kolyvagin_hypothesis(7)
False
sage: P.satisfies_kolyvagin_hypothesis(11)
False
Return the trace of this Kolyvagin point down to the real numbers, computed numerically using prec bits of working precision.
EXAMPLES:
sage: E = EllipticCurve('37a1'); P = E.kolyvagin_point(-67)
sage: P.numerical_approx()
(6.00000000000000 + 8.0...e-16*I : -15.0000000000000 - 2.96897922913431e-15*I : 1.00000000000000)
sage: P.trace_to_real_numerical()
(1.61355529131986 : -2.18446840788880 : 1.00000000000000)
sage: P.trace_to_real_numerical(prec=80)
(1.6135552913198573127230 : -2.1844684078888023289187 : 1.0000000000000000000000)
Bases: sage.structure.sage_object.SageObject
A Ring class field of a quadratic imaginary field of given conductor.
NOTE: This is a ring class field, not a ray class field. In general, the ring class field of given conductor is a subfield of the ray class field of the same conductor.
EXAMPLES:
sage: heegner_point(37,-7).ring_class_field()
Hilbert class field of QQ[sqrt(-7)]
sage: heegner_point(37,-7,5).ring_class_field()
Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: heegner_point(37,-7,55).ring_class_field()
Ring class field extension of QQ[sqrt(-7)] of conductor 55
TESTS:
sage: K_c = heegner_point(37,-7).ring_class_field()
sage: type(K_c)
<class 'sage.schemes.elliptic_curves.heegner.RingClassField'>
sage: loads(dumps(K_c)) == K_c
True
Return the absolute degree of this field over  .
.
EXAMPLES:
sage: E = EllipticCurve('389a'); K = E.heegner_point(-7,5).ring_class_field()
sage: K.absolute_degree()
12
sage: K.degree_over_K()
6
Return the conductor of this ring class field.
EXAMPLES:
sage: E = EllipticCurve('389a'); K5 = E.heegner_point(-7,5).ring_class_field()
sage: K5.conductor()
5
Return the degree of this field over the Hilbert class field  of
of  .
.
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: E.heegner_point(-59).ring_class_field().degree_over_H()
1
sage: E.heegner_point(-59).ring_class_field().degree_over_K()
3
sage: QuadraticField(-59,'a').class_number()
3
Return the relative degree of this ring class field over the
quadratic imaginary field  .
.
EXAMPLES:
sage: E = EllipticCurve('389a'); P = E.heegner_point(-7,5)
sage: K5 = P.ring_class_field(); K5
Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: K5.degree_over_K()
6
sage: type(K5.degree_over_K())
<type 'sage.rings.integer.Integer'>
sage: E = EllipticCurve('389a'); E.heegner_point(-20).ring_class_field().degree_over_K()
2
sage: E.heegner_point(-20,3).ring_class_field().degree_over_K()
4
sage: kronecker(-20,11)
-1
sage: E.heegner_point(-20,11).ring_class_field().degree_over_K()
24
Return the absolute degree of this field over  .
.
EXAMPLES:
sage: E = EllipticCurve('389a'); K = E.heegner_point(-7,5).ring_class_field()
sage: K.absolute_degree()
12
sage: K.degree_over_K()
6
Return the discriminant of the quadratic imaginary field  contained in self.
contained in self.
EXAMPLES:
sage: E = EllipticCurve('389a'); K5 = E.heegner_point(-7,5).ring_class_field()
sage: K5.discriminant_of_K()
-7
Return the Galois group of self over base.
INPUT:
- base – (default:
) a subfield of self or
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: A = E.heegner_point(-7,5).ring_class_field()
sage: A.galois_group()
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: B = E.heegner_point(-7).ring_class_field()
sage: C = E.heegner_point(-7,15).ring_class_field()
sage: A.galois_group()
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: A.galois_group(B)
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 5 over Hilbert class field of QQ[sqrt(-7)]
sage: A.galois_group().cardinality()
12
sage: A.galois_group(B).cardinality()
6
sage: C.galois_group(A)
Galois group of Ring class field extension of QQ[sqrt(-7)] of conductor 15 over Ring class field extension of QQ[sqrt(-7)] of conductor 5
sage: C.galois_group(A).cardinality()
4
Return True if this ring class field is a subfield of the ring class field 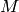 .
If
.
If 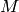 is not a ring class field, then a TypeError is raised.
is not a ring class field, then a TypeError is raised.
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: A = E.heegner_point(-7,5).ring_class_field()
sage: B = E.heegner_point(-7).ring_class_field()
sage: C = E.heegner_point(-20).ring_class_field()
sage: D = E.heegner_point(-7,15).ring_class_field()
sage: B.is_subfield(A)
True
sage: B.is_subfield(B)
True
sage: B.is_subfield(D)
True
sage: B.is_subfield(C)
False
sage: A.is_subfield(B)
False
sage: A.is_subfield(D)
True
Return the quadratic imaginary field 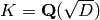 .
.
EXAMPLES:
sage: E = EllipticCurve('389a'); K = E.heegner_point(-7,5).ring_class_field()
sage: K.quadratic_field()
Number Field in sqrt_minus_7 with defining polynomial x^2 + 7
Return the primes of  that ramify in this ring class field.
that ramify in this ring class field.
EXAMPLES:
sage: E = EllipticCurve('389a'); K55 = E.heegner_point(-7,55).ring_class_field()
sage: K55.ramified_primes()
[5, 7, 11]
sage: E.heegner_point(-7).ring_class_field().ramified_primes()
[7]
Return the class number of the quadratic field with fundamental
discriminant  .
.
INPUT:
– integer
EXAMPLES:
sage: sage.schemes.elliptic_curves.heegner.class_number(-20)
2
sage: sage.schemes.elliptic_curves.heegner.class_number(-23)
3
sage: sage.schemes.elliptic_curves.heegner.class_number(-163)
1
A ValueError is raised when  is not a fundamental
discriminant:
is not a fundamental
discriminant:
sage: sage.schemes.elliptic_curves.heegner.class_number(-5)
...
ValueError: D (=-5) must be a fundamental discriminant
Return the list of self’s Heegner discriminants between -1 and -bound.
INPUT:
OUTPUT: The list of Heegner discriminants between -1 and -bound for the given elliptic curve.
EXAMPLES:
sage: E=EllipticCurve('11a')
sage: E.heegner_discriminants(30) # indirect doctest
[-7, -8, -19, -24]
Return the list of self’s first  Heegner discriminants smaller
than -5.
Heegner discriminants smaller
than -5.
INPUT:
OUTPUT: The list of the first n Heegner discriminants smaller than -5 for the given elliptic curve.
EXAMPLE:
sage: E=EllipticCurve('11a')
sage: E.heegner_discriminants_list(4) # indirect doctest
[-7, -8, -19, -24]
Returns the Heegner point on this curve associated to the
quadratic imaginary field  .
.
If the optional parameter  is given, returns the higher Heegner
point associated to the order of conductor
is given, returns the higher Heegner
point associated to the order of conductor  .
.
INPUT:
- `D` -- a Heegner discriminant
- `c` -- (default: 1) conductor, must be coprime to `DN`
- `f` -- binary quadratic form or 3-tuple `(A,B,C)` of coefficients
of `AX^2 + BXY + CY^2`
- ``check`` -- bool (default: True)
OUTPUT:
The Heegner point `y_c`.
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: E.heegner_discriminants_list(10)
[-7, -11, -40, -47, -67, -71, -83, -84, -95, -104]
sage: P = E.heegner_point(-7); P # indirect doctest
Heegner point of discriminant -7 on elliptic curve of conductor 37
sage: P.point_exact()
(0 : 0 : 1)
sage: P.curve()
Elliptic Curve defined by y^2 + y = x^3 - x over Rational Field
sage: P = E.heegner_point(-40).point_exact(); P
(a : a - 2 : 1)
sage: P = E.heegner_point(-47).point_exact(); P
(a : a^4 + a - 1 : 1)
sage: P[0].parent()
Number Field in a with defining polynomial x^5 - x^4 + x^3 + x^2 - 2*x + 1
Working out the details manually:
sage: P = E.heegner_point(-47).numerical_approx(prec=200)
sage: f = algdep(P[0], 5); f
x^5 - x^4 + x^3 + x^2 - 2*x + 1
sage: f.discriminant().factor()
47^2
The Heegner hypothesis is checked:
sage: E = EllipticCurve('389a'); P = E.heegner_point(-5,7);
...
ValueError: N (=389) and D (=-5) must satisfy the Heegner hypothesis
We can specify the quadratic form:
sage: P = EllipticCurve('389a').heegner_point(-7, 5, (778,925,275)); P
Heegner point of discriminant -7 and conductor 5 on elliptic curve of conductor 389
sage: P.quadratic_form()
778*x^2 + 925*x*y + 275*y^2
Return an interval that contains the index of the Heegner
point 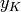 in the group of
in the group of  -rational points modulo torsion
on this elliptic curve, computed using the Gross-Zagier
formula and/or a point search, or possibly half the index
if the rank is greater than one.
-rational points modulo torsion
on this elliptic curve, computed using the Gross-Zagier
formula and/or a point search, or possibly half the index
if the rank is greater than one.
Note
If min_p is bigger than 2 then the index can be off by
any prime less than min_p. This function returns the
index divided by  exactly when the rank of
exactly when the rank of 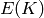 is
greater than 1 and
is
greater than 1 and 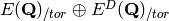 has index
has index  in
in 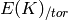 , where the second factor
undergoes a twist.
, where the second factor
undergoes a twist.
INPUT:
OUTPUT: an interval that contains the index, or half the index
EXAMPLES:
sage: E = EllipticCurve('11a')
sage: E.heegner_discriminants(50)
[-7, -8, -19, -24, -35, -39, -40, -43]
sage: E.heegner_index(-7)
1.00000?
sage: E = EllipticCurve('37b')
sage: E.heegner_discriminants(100)
[-3, -4, -7, -11, -40, -47, -67, -71, -83, -84, -95]
sage: E.heegner_index(-95) # long time (1 second)
2.00000?
This tests doing direct computation of the Mordell-Weil group.
sage: EllipticCurve('675b').heegner_index(-11)
3.0000?
Currently discriminants -3 and -4 are not supported:
sage: E.heegner_index(-3)
...
ArithmeticError: Discriminant (=-3) must not be -3 or -4.
The curve 681b returns the true index, which is 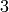 :
:
sage: E = EllipticCurve('681b')
sage: I = E.heegner_index(-8); I
3.0000?
In fact, whenever the returned index has a denominator of
 , the true index is got by multiplying the returned
index by
, the true index is got by multiplying the returned
index by  . Unfortunately, this is not an if and only if
condition, i.e., sometimes the index must be multiplied by
. Unfortunately, this is not an if and only if
condition, i.e., sometimes the index must be multiplied by
 even though the denominator is not
even though the denominator is not  .
.
This example demonstrates the 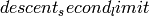 option,
which can be used to fine tune the 2-descent used to compute
the regulator of the twist:
option,
which can be used to fine tune the 2-descent used to compute
the regulator of the twist:
sage: E = EllipticCurve([0, 0, 1, -34874, -2506691])
sage: E.heegner_index(-8)
...
RuntimeError: ...
However when we search higher, we find the points we need:
sage: E.heegner_index(-8, descent_second_limit=16)
1.00000?
Assume self has rank 0.
Return a list  of primes such that if an odd prime
of primes such that if an odd prime  divides
the index of the Heegner point in the group of rational points
modulo torsion, then
divides
the index of the Heegner point in the group of rational points
modulo torsion, then  is in
is in  .
.
If 0 is in the interval of the height of the Heegner point
computed to the given prec, then this function returns 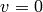 . This does not mean that the Heegner point is torsion, just
that it is very likely torsion.
. This does not mean that the Heegner point is torsion, just
that it is very likely torsion.
If we obtain no information from a search up to max_height,
e.g., if the Siksek et al. bound is bigger than max_height,
then we return 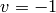 .
.
INPUT:
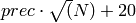 terms of
terms of  -series in computations, where
-series in computations, where  is the conductor.
is the conductor.OUTPUT:
 was automatically selected).
was automatically selected).EXAMPLES:
sage: E = EllipticCurve('11a1')
sage: E.heegner_index_bound()
([2], -7)
Return a specific Heegner point of level  with given
discriminant and conductor. If
with given
discriminant and conductor. If  is not specified, then the
first valid Heegner discriminant is used. If
is not specified, then the
first valid Heegner discriminant is used. If  is not given,
then
is not given,
then  is used.
is used.
INPUT:
– level (positive integer)
– discriminant (optional: default first valid
)
– conductor (positive integer, optional, default: 1)
EXAMPLES:
sage: heegner_point(389)
Heegner point 1/778*sqrt(-7) - 185/778 of discriminant -7 on X_0(389)
sage: heegner_point(389,-7)
Heegner point 1/778*sqrt(-7) - 185/778 of discriminant -7 on X_0(389)
sage: heegner_point(389,-7,5)
Heegner point 5/778*sqrt(-7) - 147/778 of discriminant -7 and conductor 5 on X_0(389)
sage: heegner_point(389,-20)
Heegner point 1/778*sqrt(-20) - 165/389 of discriminant -20 on X_0(389)
Use the Gross-Zagier formula to compute the Neron-Tate canonical
height over  of the Heegner point corresponding to
of the Heegner point corresponding to  , as an
interval (it’s computed to some precision using
, as an
interval (it’s computed to some precision using  -functions).
-functions).
INPUT:
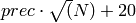 terms of
terms of  -series in computations, where
-series in computations, where  is the conductor.
is the conductor.OUTPUT: Interval that contains the height of the Heegner point.
EXAMPLE:
sage: E = EllipticCurve('11a')
sage: E.heegner_point_height(-7)
0.22227?
Return all Heegner points of given level  . Can also restrict
to Heegner points with specified discriminant
. Can also restrict
to Heegner points with specified discriminant  and optionally
conductor
and optionally
conductor  .
.
INPUT:
– level (positive integer)
– discriminant (negative integer)
– conductor (positive integer)
EXAMPLES:
sage: heegner_points(389,-7)
Set of all Heegner points on X_0(389) associated to QQ[sqrt(-7)]
sage: heegner_points(389,-7,1)
All Heegner points of conductor 1 on X_0(389) associated to QQ[sqrt(-7)]
sage: heegner_points(389,-7,5)
All Heegner points of conductor 5 on X_0(389) associated to QQ[sqrt(-7)]
Return the conjectural (analytic) order of Sha for E over the field  .
.
INPUT:
 – negative integer; the Heegner discriminant
– negative integer; the Heegner discriminantOUTPUT:
(floating point number) an approximation to the conjectural order of Sha.
Note
Often you’ll want to do proof.elliptic_curve(False) when using this function, since often the twisted elliptic curves that come up have enormous conductor, and Sha is nontrivial, which makes provably finding the Mordell-Weil group using 2-descent difficult.
EXAMPLES:
An example where E has conductor 11:
sage: E = EllipticCurve('11a')
sage: E.heegner_sha_an(-7) # long
1.00000000000000
The cache works:
sage: E.heegner_sha_an(-7) is E.heegner_sha_an(-7) # long
True
Lower precision:
sage: E.heegner_sha_an(-7,10) # long
1.0
Checking that the cache works for any precision:
sage: E.heegner_sha_an(-7,10) is E.heegner_sha_an(-7,10) # long
True
Next we consider a rank 1 curve with nontrivial Sha over the
quadratic imaginary field  ; however, there is no Sha for
; however, there is no Sha for  over
over  or for the quadratic twist of
or for the quadratic twist of  :
:
sage: E = EllipticCurve('37a')
sage: E.heegner_sha_an(-40) # long
4.00000000000000
sage: E.quadratic_twist(-40).sha().an() # long
1
sage: E.sha().an() # long
1
A rank 2 curve:
sage: E = EllipticCurve('389a') # long
sage: E.heegner_sha_an(-7) # long
1.00000000000000
If we remove the hypothesis that 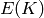 has rank 1 in Conjecture
2.3 in [Gross-Zagier, 1986, page 311], then that conjecture is
false, as the following example shows:
has rank 1 in Conjecture
2.3 in [Gross-Zagier, 1986, page 311], then that conjecture is
false, as the following example shows:
sage: E = EllipticCurve('65a') # long
sage: E.heegner_sha_an(-56) # long
1.00000000000000
sage: E.torsion_order() # long
2
sage: E.tamagawa_product() # long
1
sage: E.quadratic_twist(-56).rank() # long
2
Return True if p is an inert prime in the field 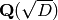 .
.
INPUT:
– fundamental discriminant
– prime integer
EXAMPLES:
sage: sage.schemes.elliptic_curves.heegner.is_inert(-7,3)
True
sage: sage.schemes.elliptic_curves.heegner.is_inert(-7,7)
False
sage: sage.schemes.elliptic_curves.heegner.is_inert(-7,11)
False
Return True if  is a Kolyvagin conductor for level
is a Kolyvagin conductor for level  ,
discriminant
,
discriminant  , mod
, mod  , etc., i.e.,
, etc., i.e.,  is divisible by exactly
is divisible by exactly
 prime factors, is coprime to
prime factors, is coprime to 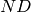 , each prime dividing
, each prime dividing  is
inert, and if
is
inert, and if  is not None then
is not None then  for each prime
for each prime  dividing
dividing  .
.
INPUT:
– level (positive integer)
– elliptic curve or None
– negative fundamental discriminant
– number of prime factors (nonnegative integer) or None
– torsion order (i.e., do we get class in
?)
– conductor (positive integer)
EXAMPLES:
sage: from sage.schemes.elliptic_curves.heegner import is_kolyvagin_conductor
sage: is_kolyvagin_conductor(389,None,-7,1,None,5)
True
sage: is_kolyvagin_conductor(389,None,-7,1,None,7)
False
sage: is_kolyvagin_conductor(389,None,-7,1,None,11)
False
sage: is_kolyvagin_conductor(389,EllipticCurve('389a'),-7,1,3,5)
True
sage: is_kolyvagin_conductor(389,EllipticCurve('389a'),-7,1,11,5)
False
Return True if p is a ramified prime in the field 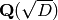 .
.
INPUT:
– fundamental discriminant
– prime integer
EXAMPLES:
sage: sage.schemes.elliptic_curves.heegner.is_ramified(-7,2)
False
sage: sage.schemes.elliptic_curves.heegner.is_ramified(-7,7)
True
sage: sage.schemes.elliptic_curves.heegner.is_ramified(-1,2)
True
Return True if p is a split prime in the field 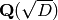 .
.
INPUT:
– fundamental discriminant
– prime integer
EXAMPLES:
sage: sage.schemes.elliptic_curves.heegner.is_split(-7,3)
False
sage: sage.schemes.elliptic_curves.heegner.is_split(-7,7)
False
sage: sage.schemes.elliptic_curves.heegner.is_split(-7,11)
True
Returns the Kolyvagin point on this curve associated to the
quadratic imaginary field  and conductor
and conductor  .
.
INPUT:
– a Heegner discriminant
– (default: 1) conductor, must be coprime to
- check – bool (default: True)
OUTPUT:
The Kolyvagin pointof conductor
.
EXAMPLES:
sage: E = EllipticCurve('37a1')
sage: P = E.kolyvagin_point(-67); P
Kolyvagin point of discriminant -67 on elliptic curve of conductor 37
sage: P.numerical_approx()
(6.00000000000000 + 8.0...e-16*I : -15.0000000000000 - 2.96897922913431e-15*I : 1.00000000000000)
sage: P.index()
6
sage: g = E((0,-1,1)) # a generator
sage: E.regulator() == E.regulator_of_points([g])
True
sage: 6*g
(6 : -15 : 1)
Given an elliptic curve of positive rank and a prime  , this
function returns data about how to use Kolyvagin’s
, this
function returns data about how to use Kolyvagin’s  -torsion
Heegner point Euler system to do computations with this curve.
See the precise description of the output below.
-torsion
Heegner point Euler system to do computations with this curve.
See the precise description of the output below.
INPUT:
– elliptic curve over
of rank 1 or 2
– an odd prime that doesn’t divide the order of the
rational torsion subgroup of
- first_only – bool (default: True) whether two only return
the first prime that one can work modulo to get data about the Euler system
OUTPUT in the rank 1 case or when the default flag first_only=True:
– first good odd prime satisfying the Kolyvagin
condition that
divides gcd(a_{ell},ell+1)` and the reduction map is surjective to
– discriminant of the first quadratic imaginary field
that satisfies the Heegner hypothesis for
such that both
is inert in
, and the twist
has analytic rank
– the class number of
the dimension of the Brandt module
, where
is the conductor of
OUTPUT in the rank 2 case:
– first prime (as above in the rank 1 case) where reduction map is surjective
– second prime (as above) where reduction map is surjective
– discriminant of the first quadratic imaginary field
that satisfies the Heegner hypothesis for
such that both
and
are simultaneously inert in
, and the twist
has analytic rank
– the class number of
the dimension of the Brandt module
, where
is the conductor of
the dimension of the Brandt module
EXAMPLES:
Import this function:
sage: from sage.schemes.elliptic_curves.heegner import kolyvagin_reduction_data
A rank 1 example:
sage: kolyvagin_reduction_data(EllipticCurve('37a1'),3)
(17, -7, 1, 52)
A rank 3 example:
sage: kolyvagin_reduction_data(EllipticCurve('5077a1'),3)
(11, -47, 5, 4234)
sage: H = heegner_points(5077, -47)
sage: [c for c in H.kolyvagin_conductors(2,10,EllipticCurve('5077a1'),3) if c%11]
[667, 943, 1189, 2461]
sage: factor(667)
23 * 29
A rank 4 example (the first Kolyvagin class that we could try to
compute would be 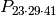 , and would require
working in a space of dimension 293060 (so prohibitive at
present):
, and would require
working in a space of dimension 293060 (so prohibitive at
present):
sage: E = elliptic_curves.rank(4)[0]
sage: kolyvagin_reduction_data(E,3) # long
(11, -71, 7, 293060)
sage: H = heegner_points(293060, -71)
sage: H.kolyvagin_conductors(1,4,E,3)
[11, 17, 23, 41]
The first rank 2 example:
sage: kolyvagin_reduction_data(EllipticCurve('389a'),3)
(5, -7, 1, 130)
sage: kolyvagin_reduction_data(EllipticCurve('389a'),3, first_only=False)
(5, 17, -7, 1, 130, 520)
A large 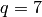 :
:
sage: kolyvagin_reduction_data(EllipticCurve('1143c1'),7, first_only=False)
(13, 83, -59, 3, 1536, 10496)
Additive reduction:
sage: kolyvagin_reduction_data(EllipticCurve('2350g1'),5, first_only=False)
(19, 239, -311, 19, 6480, 85680)
make_monic returns a monic integral polynomial  and an
integer
and an
integer  such that if
such that if 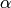 is a root of
is a root of 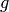 then a root of
then a root of
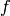 is
is 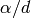 .
.
INPUT:
- f – polynomial over the rational numbers
EXAMPLES:
sage: R.<x> = QQ[]
sage: sage.schemes.elliptic_curves.heegner.make_monic(3*x^3 + 14*x^2 - 7*x + 5)
(x^3 + 14*x^2 - 21*x + 45, 3)
In this example we verify that make_monic does what we claim it does:
sage: K.<a> = NumberField(x^3 + 17*x - 3)
sage: f = (a/7+2/3).minpoly(); f
x^3 - 2*x^2 + 247/147*x - 4967/9261
sage: g, d = sage.schemes.elliptic_curves.heegner.make_monic(f)
sage: g
x^3 - 18522*x^2 + 144110421*x - 426000323007
sage: d
9261
sage: K.<b> = NumberField(g)
sage: (b/d).minpoly()
x^3 - 2*x^2 + 247/147*x - 4967/9261
Return a polynomial whose coefficients are rational numbers close
to the coefficients of 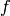 .
.
INPUT:
– polynomial with real floating point entries
- **kwds – passed on to nearby_rational method
EXAMPLES:
sage: R.<x> = RR[]
sage: sage.schemes.elliptic_curves.heegner.nearby_rational_poly(2.1*x^2 + 3.5*x - 1.2, max_error=10e-16)
21/10*X^2 + 7/2*X - 6/5
sage: sage.schemes.elliptic_curves.heegner.nearby_rational_poly(2.1*x^2 + 3.5*x - 1.2, max_error=10e-17)
4728779608739021/2251799813685248*X^2 + 7/2*X - 5404319552844595/4503599627370496
sage: RR(4728779608739021/2251799813685248 - 21/10)
8.88178419700125e-17
Return order of conductor  in quadratic field with fundamental
discriminant
in quadratic field with fundamental
discriminant  .
.
INPUT:
– fundamental discriminant
– conductor
- names – string (default: ‘a’)
OUTPUT:
- order
of conductor
in an imaginary quadratic field
- the element
as an element of
The generator for the field is named ‘a’ by default.
EXAMPLES:
sage: sage.schemes.elliptic_curves.heegner.quadratic_order(-7,3)
(Order in Number Field in a with defining polynomial x^2 + 7, 3*a)
sage: sage.schemes.elliptic_curves.heegner.quadratic_order(-7,3,'alpha')
(Order in Number Field in alpha with defining polynomial x^2 + 7, 3*alpha)
Returns True precisely when  is a fundamental discriminant that
satisfies the Heegner hypothesis for this elliptic curve.
is a fundamental discriminant that
satisfies the Heegner hypothesis for this elliptic curve.
EXAMPLES:
sage: E = EllipticCurve('11a1')
sage: E.satisfies_heegner_hypothesis(-7)
True
sage: E.satisfies_heegner_hypothesis(-11)
False
Check that  satisfies the weak Heegner hypothesis relative to
satisfies the weak Heegner hypothesis relative to  .
This is all that is needed to define Heegner points.
.
This is all that is needed to define Heegner points.
The condition is that  is a fundamental discriminant and that
each unramified prime dividing
is a fundamental discriminant and that
each unramified prime dividing  splits in
splits in  and
each ramified prime exactly divides
and
each ramified prime exactly divides  . We also do not require
that
. We also do not require
that  .
.
INPUT:
– positive integer
– negative integer
EXAMPLES:
sage: s = sage.schemes.elliptic_curves.heegner.satisfies_weak_heegner_hypothesis
sage: s(37,-7)
True
sage: s(37,-37)
False
sage: s(37,-37*4)
True
sage: s(100,-4)
False
sage: [D for D in [-1,-2,..,-40] if s(37,D)]
[-3, -4, -7, -11, -40]
sage: [D for D in [-1,-2,..,-100] if s(37,D)]
[-3, -4, -7, -11, -40, -47, -67, -71, -83, -84, -95]
sage: EllipticCurve('37a').heegner_discriminants_list(10)
[-7, -11, -40, -47, -67, -71, -83, -84, -95, -104]
Return a polynomial whose coefficients are as simple as possible rationals that are also close to the coefficients of f.
INPUT:
– polynomial with real floating point entries
- prec – positive integer
EXAMPLES:
sage: R.<x> = RR[]
sage: sage.schemes.elliptic_curves.heegner.simplest_rational_poly(2.1*x^2 + 3.5*x - 1.2, 53)
21/10*X^2 + 7/2*X - 6/5