Quotients of Univariate Polynomial Rings

EXAMPLES:

sage: R.<x> = QQ[]
sage: S = R.quotient(x**3-3*x+1, 'alpha')
sage: S.gen()**2 in S
True
sage: x in S
True
sage: S.gen() in R
False
sage: 1 in S
True

sage.rings.polynomial.polynomial_quotient_ring.PolynomialQuotientRing(ring, polynomial, names=None)

Create a quotient of a polynomial ring.

INPUT:

• ring - a univariate polynomial ring in one variable.
• polynomial - element
• names - (optional) name for the variable

OUTPUT: Creates the quotient ring R/I, where R is the ring and I is the principal ideal generated by the polynomial.

EXAMPLES:

We create the quotient ring , and demonstrate many basic functions with it:

sage: Z = IntegerRing()
sage: R = PolynomialRing(Z,'x'); x = R.gen()
sage: S = R.quotient(x^3 + 7, 'a'); a = S.gen()
sage: S
Univariate Quotient Polynomial Ring in a over Integer Ring with modulus x^3 + 7
sage: a^3
-7
sage: S.is_field()
False
sage: a in S
True
sage: x in S
True
sage: a in R
False
sage: S.polynomial_ring()
Univariate Polynomial Ring in x over Integer Ring
sage: S.modulus()
x^3 + 7
sage: S.degree()
3

We create the “iterated” polynomial ring quotient

sage: A.<y> = PolynomialRing(GF(2)); A
Univariate Polynomial Ring in y over Finite Field of size 2 (using NTL)
sage: B = A.quotient(y^2 + y + 1, 'y2'); print B
Univariate Quotient Polynomial Ring in y2 over Finite Field of size 2 with modulus y^2 + y + 1
sage: C = PolynomialRing(B, 'x'); x=C.gen(); print C
Univariate Polynomial Ring in x over Univariate Quotient Polynomial Ring in y2 over Finite Field of size 2 with modulus y^2 + y + 1
sage: R = C.quotient(x^3 - 5); print R
Univariate Quotient Polynomial Ring in xbar over Univariate Quotient Polynomial Ring in y2 over Finite Field of size 2 with modulus y^2 + y + 1 with modulus x^3 + 1

Next we create a number field, but viewed as a quotient of a polynomial ring over :

sage: R = PolynomialRing(RationalField(), 'x'); x = R.gen()
sage: S = R.quotient(x^3 + 2*x - 5, 'a')
sage: S
Univariate Quotient Polynomial Ring in a over Rational Field with modulus x^3 + 2*x - 5
sage: S.is_field()
True
sage: S.degree()
3

There are conversion functions for easily going back and forth between quotients of polynomial rings over and number fields:

sage: K = S.number_field(); K
Number Field in a with defining polynomial x^3 + 2*x - 5
sage: K.polynomial_quotient_ring()
Univariate Quotient Polynomial Ring in a over Rational Field with modulus x^3 + 2*x - 5

The leading coefficient must be a unit (but need not be 1).

sage: R = PolynomialRing(Integers(9), 'x'); x = R.gen()
sage: S = R.quotient(2*x^4 + 2*x^3 + x + 2, 'a')
sage: S = R.quotient(3*x^4 + 2*x^3 + x + 2, 'a')
...
TypeError: polynomial must have unit leading coefficient

Another example:

sage: R.<x> = PolynomialRing(IntegerRing())
sage: f = x^2 + 1
sage: R.quotient(f)
Univariate Quotient Polynomial Ring in xbar over Integer Ring with modulus x^2 + 1

This shows that the issue at trac 5482 is solved:

sage: R.<x> = PolynomialRing(QQ)
sage: f = x^2-1
sage: R.quotient_by_principal_ideal(f)
Univariate Quotient Polynomial Ring in xbar over Rational Field with modulus x^2 - 1

class sage.rings.polynomial.polynomial_quotient_ring.PolynomialQuotientRing_domain(ring, polynomial, name=None)

Bases: sage.rings.polynomial.polynomial_quotient_ring.PolynomialQuotientRing_generic, sage.rings.ring.IntegralDomain

EXAMPLES:

sage: R.<x> = PolynomialRing(ZZ)
sage: S.<xbar> = R.quotient(x^2 + 1)
sage: S
Univariate Quotient Polynomial Ring in xbar over Integer Ring with modulus x^2 + 1
sage: loads(S.dumps()) == S
True
sage: loads(xbar.dumps()) == xbar
True

field_extension(names)

Takes a polynomial quotient ring, and returns a tuple with three elements: the NumberField defined by the same polynomial quotient ring, a homomorphism from its parent to the NumberField sending the generators to one another, and the inverse isomorphism.

OUTPUT:

• field
• homomorphism from self to field
• homomorphism from field to self

EXAMPLES:

sage: R.<x> = PolynomialRing(Rationals())
sage: S.<alpha> = R.quotient(x^3-2)
sage: F.<b>, f, g = S.field_extension()
sage: F
Number Field in b with defining polynomial x^3 - 2
sage: a = F.gen()
sage: f(alpha)
b
sage: g(a)
alpha

Note that the parent ring must be an integral domain:

sage: R.<x> = GF(25,'f25')['x']
sage: S.<a> = R.quo(x^3 - 2)
sage: F, g, h = S.field_extension('b')
...
AttributeError: 'PolynomialQuotientRing_generic' object has no attribute 'field_extension'

Over a finite field, the corresponding field extension is not a number field:

sage: R.<x> = GF(25, 'a')['x']
sage: S.<a> = R.quo(x^3 + 2*x + 1)
sage: F, g, h = S.field_extension('b')
sage: h(F.0^2 + 3)
a^2 + 3
sage: g(x^2 + 2)
b^2 + 2

We do an example involving a relative number field:

sage: R.<x> = QQ['x']
sage: K.<a> = NumberField(x^3 - 2)
sage: S.<X> = K['X']
sage: Q.<b> = S.quo(X^3 + 2*X + 1)
sage: Q.field_extension('b')
(Number Field in b with defining polynomial X^3 + 2*X + 1 over its base field, ...
  Defn: b |--> b, Relative number field morphism:
  From: Number Field in b with defining polynomial X^3 + 2*X + 1 over its base field
  To:   Univariate Quotient Polynomial Ring in b over Number Field in a with defining polynomial x^3 - 2 with modulus X^3 + 2*X + 1
  Defn: b |--> b
        a |--> a)

We slightly change the example above so it works.

sage: R.<x> = QQ['x']
sage: K.<a> = NumberField(x^3 - 2)
sage: S.<X> = K['X']
sage: f = (X+a)^3 + 2*(X+a) + 1
sage: f
X^3 + 3*a*X^2 + (3*a^2 + 2)*X + 2*a + 3
sage: Q.<z> = S.quo(f)
sage: F.<w>, g, h = Q.field_extension()
sage: c = g(z)
sage: f(c)
0
sage: h(g(z))
z
sage: g(h(w))
w        

AUTHORS:

• Craig Citro (2006-08-07)
• William Stein (2006-08-06)

is_finite()

Return whether or not this quotient ring is finite.

EXAMPLES:

sage: R.<x> = ZZ[]
sage: R.quo(1).is_finite()
True
sage: R.quo(x^3-2).is_finite()
False

sage: R.<x> = GF(9,'a')[]
sage: R.quo(2*x^3+x+1).is_finite()
True
sage: R.quo(2).is_finite()
True

class sage.rings.polynomial.polynomial_quotient_ring.PolynomialQuotientRing_field(ring, polynomial, name=None)

Bases: sage.rings.polynomial.polynomial_quotient_ring.PolynomialQuotientRing_domain, sage.rings.ring.Field

EXAMPLES:

sage: R.<x> = PolynomialRing(QQ)
sage: S.<xbar> = R.quotient(x^2 + 1)
sage: S
Univariate Quotient Polynomial Ring in xbar over Rational Field with modulus x^2 + 1        
sage: loads(S.dumps()) == S
True
sage: loads(xbar.dumps()) == xbar
True

base_field()

Alias for base_ring, when we’re defined over a field.

complex_embeddings(prec=53)

Return all homomorphisms of this ring into the approximate complex field with precision prec.

EXAMPLES:

sage: R.<x> = QQ[]
sage: f = x^5 + x + 17
sage: k = R.quotient(f)
sage: v = k.complex_embeddings(100)
sage: [phi(k.0^2) for phi in v]
[2.9757207403766761469671194565, -2.4088994371613850098316292196 + 1.9025410530350528612407363802*I, -2.4088994371613850098316292196 - 1.9025410530350528612407363802*I, 0.92103906697304693634806949137 - 3.0755331188457794473265418086*I, 0.92103906697304693634806949137 + 3.0755331188457794473265418086*I]

class sage.rings.polynomial.polynomial_quotient_ring.PolynomialQuotientRing_generic(ring, polynomial, name=None)

Bases: sage.rings.ring.CommutativeRing

Quotient of a univariate polynomial ring by an ideal.

EXAMPLES:

sage: R.<x> = PolynomialRing(Integers(8)); R
Univariate Polynomial Ring in x over Ring of integers modulo 8
sage: S.<xbar> = R.quotient(x^2 + 1); S
Univariate Quotient Polynomial Ring in xbar over Ring of integers modulo 8 with modulus x^2 + 1

We demonstrate object persistence.

sage: loads(S.dumps()) == S
True
sage: loads(xbar.dumps()) == xbar
True

We create some sample homomorphisms;

sage: R.<x> = PolynomialRing(ZZ)
sage: S = R.quo(x^2-4)
sage: f = S.hom([2])
sage: f
Ring morphism:
  From: Univariate Quotient Polynomial Ring in xbar over Integer Ring with modulus x^2 - 4
  To:   Integer Ring
  Defn: xbar |--> 2        
sage: f(x)
2
sage: f(x^2 - 4)
0
sage: f(x^2)
4

S_class_group(S, proof=True)

If this quotient ring is over a number field K, by a polynomial with nonzero discriminant, and S is a set of primes of K, this function returns a list of representatives which generate the S-class group.

NOTE:

Since the ideal function behaves differently over number fields than over polynomial quotient rings (i.e. the quotient does not even know its ring of integers), we return a set of generators of each ideal. The format for each generator is (gen, order, pr), where order is the multiplicative order of gen, i.e. gen^order is a principal ideal, gen is a tuple of generators of the representative ideal, and pr is a generator of the principal ideal gen^order.

INPUT:

• S - a set of primes of the coefficient ring
• proof - if False, assume Pari’s GRH++ in computing the class group

OUTPUT:

A list of tuples (gen, order, pr), where gen is a tuple of elements which generate a fractional ideal representative of the class group generator of order order, and pr is a principal generator of .

EXAMPLES:

A trivial algebra over 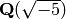has the same class group as its base:

sage: K.<a> = QuadraticField(-5)
sage: R.<x> = K[]
sage: S.<xbar> = R.quotient(x)
sage: S.S_class_group([])
[((2, -a + 1), 2, 2)]

When we include the prime , the S-class group becomes trivial:

sage: S.S_class_group([K.ideal(2, -a+1)])
[]

Here is an example where the base and the extension both contribute to the class group:

sage: K.<a> = QuadraticField(-5)
sage: K.class_group()
Class group of order 2 with structure C2 of Number Field in a with defining polynomial x^2 + 5
sage: R.<x> = K[]
sage: S.<xbar> = R.quotient(x^2 + 23)
sage: S.S_class_group([])
[((3, -3*a, 3/2*xbar - 3/2, (-1/2*a + 1)*xbar - 1/2*a + 1),
  6,
  (1/2*a - 101/2)*xbar + 187/2*a + 67/2)]
sage: S.S_class_group([K.ideal(3, a-1)])
[]
sage: S.S_class_group([K.ideal(2, a+1)])
[]
sage: S.S_class_group([K.ideal(a)])
[((3, -3*a, 3/2*xbar - 3/2, (-1/2*a + 1)*xbar - 1/2*a + 1),
  6,
  (1/2*a - 101/2)*xbar + 187/2*a + 67/2)]

Now we take an example over a nontrivial base with two factors, each contributing to the class group:

sage: K.<a> = QuadraticField(-5)
sage: R.<x> = K[]
sage: S.<xbar> = R.quotient((x^2 + 23)*(x^2 + 31))
sage: S.S_class_group([])
[((3/8*xbar^2 + 93/8,
   -3/8*a*xbar^2 - 93/8*a, 3/16*xbar^3 - 3/16*xbar^2 + 93/16*xbar - 93/16,
   (-1/16*a + 1/8)*xbar^3 + (-1/16*a + 1/8)*xbar^2 + (-31/16*a + 31/8)*xbar - 31/16*a + 31/8),
  6,
  (1/16*a - 101/16)*xbar^3 + (187/16*a + 65/16)*xbar^2 + (31/16*a - 3131/16)*xbar + 5797/16*a + 2031/16),
 ((-1/4*xbar^2 - 23/4,
   (1/8*a - 1/8)*xbar^2 + 23/8*a - 23/8,
   -1/16*xbar^3 ...xbar^2 - 23/16*xbar ...,
   1/16*a*xbar^3 ...xbar^2 + 23/16*a*xbar ...),
  6,
  1/16*xbar^3 + 1/16*xbar^2 + 23/16*xbar + 39/16),
 ((-5/4*xbar^2 - 115/4,
   5/4*a*xbar^2 + 115/4*a,
   -5/16*xbar^3 - 5/16*xbar^2 - 115/16*xbar - 115/16,   
   1/16*a*xbar^3 + 13/16*a*xbar^2 + 23/16*a*xbar + 299/16*a),
  2,
  5/16*xbar^3 - 33/16*xbar^2 + 115/16*xbar - 743/16)]   

By using the ideal , we cut the part of the class group coming from 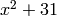from 12 to 2, i.e. we lose a generator of order 6:

sage: S.S_class_group([K.ideal(a)])
[((3/8*xbar^2 + 93/8,
   -3/8*a*xbar^2 - 93/8*a,
   3/16*xbar^3 - 3/16*xbar^2 + 93/16*xbar - 93/16,
   (-1/16*a + 1/8)*xbar^3 + (-1/16*a + 1/8)*xbar^2 + (-31/16*a + 31/8)*xbar - 31/16*a + 31/8),
  6,
  (...1/16*a ... 101/16)*xbar^3 + (...187/16*a ...)*xbar^2 + (...31/16*a ... 3131/16)*xbar ... 5797/16*a ...),
 ((-1/4*xbar^2 - 23/4,
   (1/8*a - 1/8)*xbar^2 + 23/8*a - 23/8,
   -1/16*xbar^3 ...,
   1/16*a*xbar^3 ...),
  2,
  -1/8*xbar^2 - 15/8)]

Note that all the returned values live where we expect them to:

sage: CG = S.S_class_group([])
sage: type(CG[0][0][1])
<class 'sage.rings.polynomial.polynomial_quotient_ring_element.PolynomialQuotientRingElement'>
sage: type(CG[0][1])
<type 'sage.rings.integer.Integer'>
sage: type(CG[0][2])
<class 'sage.rings.polynomial.polynomial_quotient_ring_element.PolynomialQuotientRingElement'>

S_units(S, proof=True)

If this quotient ring is over a number field K, by a polynomial with nonzero discriminant, and S is a set of primes of K, this function returns a list of generators of the S-units.

INPUT:

- ``S`` - a set of primes of the coefficient ring

• proof - if False, assume Pari’s GRH++ in computing the class group

OUTPUT:

A list of generators of the unit group, in the form (gen, order), where gen is a unit of order order.

EXAMPLES:

sage: K.<a> = QuadraticField(-3)
sage: K.unit_group()
Unit group with structure C6 of Number Field in a with defining polynomial x^2 + 3
sage: K.<a> = QQ['x'].quotient(x^2 + 3)
sage: u,o = K.S_units([])[0]; u, o
(-1/2*a + 1/2, 6)
sage: u^6
1
sage: u^3
-1
sage: u^2
-1/2*a - 1/2

sage: K.<a> = QuadraticField(-3)
sage: y = polygen(K)
sage: L.<b> = K['y'].quotient(y^3 + 5); L
Univariate Quotient Polynomial Ring in b over Number Field in a with defining polynomial x^2 + 3 with modulus y^3 + 5
sage: L.S_units([])
[(-1/2*a + 1/2, 6),
 ((...1/3*a - 1)*b^2 + ...*b + ...*a + ..., +Infinity),
 ((...1/3*a + 1)*b^2 ...*b ...*a ..., +Infinity)]
sage: L.S_units([K.ideal(1/2*a - 3/2)])
[((...1/6*a - 1/2)*b^2 + (...1/3*a + 1)*b ... 2/3*a - 2, +Infinity),
 (-1/2*a + 1/2, 6),
 ((-1/3*a + 1)*b^2 + (2/3*a - 2)*b - 5/6*a + 7/2, +Infinity),
 ((...1/3*a ... 1)*b^2 + (...2/3*a - 2)*b + ...*a + ..., +Infinity)]
sage: L.S_units([K.ideal(2)])
[((...*a ... 1/2)*b^2 + (...a ... 1)*b + ...*a ... 3/2, +Infinity),
 ((1/6*a + 1/2)*b^2 + (-1/3*a - 1)*b + 1/6*a + 3/2, +Infinity),
 ((...*a + 1/2)*b^2 + (...a - 1)*b ...*a + ..., +Infinity),
 (-1/2*a + 1/2, 6),
 ((-1/3*a + 1)*b^2 + (2/3*a - 2)*b - 5/6*a + 7/2, +Infinity),
 ((-1/3*a + 1)*b^2 - 4/3*a*b - 4/3*a - 3, +Infinity)]   

Note that all the returned values live where we expect them to:

sage: U = L.S_units([])
sage: type(U[0][0])
<class 'sage.rings.polynomial.polynomial_quotient_ring_element.PolynomialQuotientRingElement'>
sage: type(U[0][1])
<type 'sage.rings.integer.Integer'>
sage: type(U[1][1])
<class 'sage.rings.infinity.PlusInfinity'>

base_ring()

Return the base ring of the polynomial ring, of which this ring is a quotient.

EXAMPLES:

The base ring of is .

sage: R.<z> = PolynomialRing(ZZ)
sage: S.<beta> = R.quo(z^3 + z^2 + z + 1)
sage: S.base_ring()
Integer Ring

Next we make a polynomial quotient ring over 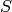and ask for its base ring.

sage: T.<t> = PolynomialRing(S)
sage: W = T.quotient(t^99 + 99)
sage: W.base_ring()
Univariate Quotient Polynomial Ring in beta over Integer Ring with modulus z^3 + z^2 + z + 1

characteristic()

Return the characteristic of this quotient ring.

This is always the same as the characteristic of the base ring.

EXAMPLES:

sage: R.<z> = PolynomialRing(ZZ)
sage: S.<a> = R.quo(z - 19)
sage: S.characteristic()
0
sage: R.<x> = PolynomialRing(GF(9,'a'))
sage: S = R.quotient(x^3 + 1)
sage: S.characteristic()
3

class_group(proof=True)

If this quotient ring is over a number field K, by a polynomial of nonzero discriminant, returns a list of representatives which generate the class group.

NOTE:

Since the ideal function behaves differently over number fields than over polynomial quotient rings (i.e. the quotient does not even know its ring of integers), we return a set of generators of each ideal. The format for each generator is (gen, order, pr), where order is the multiplicative order of gen, i.e. gen^order is a principal ideal, gen is a tuple of generators of the representative ideal, and pr is a generator of the principal ideal gen^order.

INPUT:

- ``proof`` - if False, assume Pari's GRH++ in computing the class group

OUTPUT:

A list of tuples (gen, order, pr), where gen is a tuple of elements which generate a fractional ideal representative of the class group generator of order order, and pr is a principal generator of .

EXAMPLES::

sage: K.<a> = QuadraticField(-3) sage: K.class_group() Class group of order 1 with structure of Number Field in a with defining polynomial x^2 + 3 sage: K.<a> = QQ[‘x’].quotient(x^2 + 3) sage: K.class_group() []

A trivial algebra over 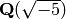has the same class group as its base:

sage: K.<a> = QuadraticField(-5)
sage: R.<x> = K[]
sage: S.<xbar> = R.quotient(x)
sage: S.class_group()
[((2, -a + 1), 2, 2)]

Here is an example where the base and the extension both contribute to the class group:

sage: K.<a> = QuadraticField(-5)
sage: K.class_group()
Class group of order 2 with structure C2 of Number Field in a with defining polynomial x^2 + 5
sage: R.<x> = K[]
sage: S.<xbar> = R.quotient(x^2 + 23)
sage: S.class_group()
[((3, -3*a, 3/2*xbar - 3/2, (-1/2*a + 1)*xbar - 1/2*a + 1),
  6,
  (1/2*a - 101/2)*xbar + 187/2*a + 67/2)]

Here is an example of a product of number fields, both of which contribute to the class group:

sage: R.<x> = QQ[]
sage: S.<xbar> = R.quotient((x^2 + 23)*(x^2 + 47))
sage: S.class_group()
[((1/12*xbar^2 + 47/12,
   1/48*xbar^3 - 1/48*xbar^2 + 47/48*xbar - 47/48),
  3,
  -1/48*xbar^3 - 5/48*xbar^2 - 47/48*xbar - 187/48),
 ((-1/12*xbar^2 - 23/12,
   -1/48*xbar^3 - ...xbar^2 - 23/48*xbar - ...),
  5,
  -1/48*xbar^3 ...xbar^2 - 23/48*xbar ...)]

Now we take an example over a nontrivial base with two factors, each contributing to the class group:

sage: K.<a> = QuadraticField(-5)
sage: R.<x> = K[]
sage: S.<xbar> = R.quotient((x^2 + 23)*(x^2 + 31))
sage: S.class_group()
[((3/8*xbar^2 + 93/8,
   -3/8*a*xbar^2 - 93/8*a, 3/16*xbar^3 - 3/16*xbar^2 + 93/16*xbar - 93/16,
   (-1/16*a + 1/8)*xbar^3 + (-1/16*a + 1/8)*xbar^2 + (-31/16*a + 31/8)*xbar - 31/16*a + 31/8),
  6,
  (1/16*a - 101/16)*xbar^3 + (187/16*a + 65/16)*xbar^2 + (31/16*a - 3131/16)*xbar + 5797/16*a + 2031/16),
 ((-1/4*xbar^2 - 23/4,
   (1/8*a - 1/8)*xbar^2 + 23/8*a - 23/8,
   -1/16*xbar^3 ...,
   1/16*a*xbar^3 ...),
  6,
  1/16*xbar^3 + 1/16*xbar^2 + 23/16*xbar + 39/16),
 ((-5/4*xbar^2 - 115/4,
   5/4*a*xbar^2 + 115/4*a,
   -5/16*xbar^3 - 5/16*xbar^2 - 115/16*xbar - 115/16,  
   1/16*a*xbar^3 + 13/16*a*xbar^2 + 23/16*a*xbar + 299/16*a),
  2,
  5/16*xbar^3 - 33/16*xbar^2 + 115/16*xbar - 743/16)]

Note that all the returned values live where we expect them to:

sage: CG = S.class_group()
sage: type(CG[0][0][1])
<class 'sage.rings.polynomial.polynomial_quotient_ring_element.PolynomialQuotientRingElement'>
sage: type(CG[0][1])
<type 'sage.rings.integer.Integer'>
sage: type(CG[0][2])
<class 'sage.rings.polynomial.polynomial_quotient_ring_element.PolynomialQuotientRingElement'>

cover_ring()

Return the polynomial ring of which this ring is the quotient.

EXAMPLES:

sage: R.<x> = PolynomialRing(QQ)
sage: S = R.quotient(x^2-2)
sage: S.polynomial_ring()
Univariate Polynomial Ring in x over Rational Field

degree()

Return the degree of this quotient ring. The degree is the degree of the polynomial that we quotiented out by.

EXAMPLES:

sage: R.<x> = PolynomialRing(GF(3))
sage: S = R.quotient(x^2005 + 1)
sage: S.degree()
2005

discriminant(v=None)

Return the discriminant of this ring over the base ring. This is by definition the discriminant of the polynomial that we quotiented out by.

EXAMPLES:

sage: R.<x> = PolynomialRing(QQ)
sage: S = R.quotient(x^3 + x^2 + x + 1)
sage: S.discriminant()
-16
sage: S = R.quotient((x + 1) * (x + 1))
sage: S.discriminant()
0

The discriminant of the quotient polynomial ring need not equal the discriminant of the corresponding number field, since the discriminant of a number field is by definition the discriminant of the ring of integers of the number field:

sage: S = R.quotient(x^2 - 8)
sage: S.number_field().discriminant()
8
sage: S.discriminant()
32

gen(n=0)

Return the generator of this quotient ring. This is the equivalence class of the image of the generator of the polynomial ring.

EXAMPLES:

sage: R.<x> = PolynomialRing(QQ)
sage: S = R.quotient(x^2 - 8, 'gamma')
sage: S.gen()
gamma

is_field(proof=True)

Return whether or not this quotient ring is a field.

EXAMPLES:

sage: R.<z> = PolynomialRing(ZZ)
sage: S = R.quo(z^2-2)
sage: S.is_field()
False
sage: R.<x> = PolynomialRing(QQ)
sage: S = R.quotient(x^2 - 2)
sage: S.is_field()
True

krull_dimension()

modulus()

Return the polynomial modulus of this quotient ring.

EXAMPLES:

sage: R.<x> = PolynomialRing(GF(3))
sage: S = R.quotient(x^2 - 2)
sage: S.modulus()
x^2 + 1

ngens()

Return the number of generators of this quotient ring over the base ring. This function always returns 1.

EXAMPLES:

sage: R.<x> = PolynomialRing(QQ)
sage: S.<y> = PolynomialRing(R)
sage: T.<z> = S.quotient(y + x)
sage: T
Univariate Quotient Polynomial Ring in z over Univariate Polynomial Ring in x over Rational Field with modulus y + x
sage: T.ngens()
1

number_field()

Return the number field isomorphic to this quotient polynomial ring, if possible.

EXAMPLES:

sage: R.<x> = PolynomialRing(QQ)
sage: S.<alpha> = R.quotient(x^29 - 17*x - 1)
sage: K = S.number_field()
sage: K
Number Field in alpha with defining polynomial x^29 - 17*x - 1
sage: alpha = K.gen()
sage: alpha^29
17*alpha + 1

order()

Return the number of elements of this quotient ring.

EXAMPLES:

sage: F1.<a> = GF(2^7)
sage: P1.<x> = F1[]
sage: F2 = F1.extension(x^2+x+1, 'u')
sage: F2.order()
16384

sage: F1 = QQ
sage: P1.<x> = F1[]
sage: F2 = F1.extension(x^2+x+1, 'u')
sage: F2.order()
+Infinity

polynomial_ring()

Return the polynomial ring of which this ring is the quotient.

EXAMPLES:

sage: R.<x> = PolynomialRing(QQ)
sage: S = R.quotient(x^2-2)
sage: S.polynomial_ring()
Univariate Polynomial Ring in x over Rational Field

random_element(*args, **kwds)

Return a random element of this quotient ring.

INPUT:

• *args, **kwds - Arguments for randomization that are passed on to the random_element method of the polynomial ring, and from there to the base ring

OUTPUT:

• Element of this quotient ring

EXAMPLES:

sage: F1.<a> = GF(2^7)
sage: P1.<x> = F1[]
sage: F2 = F1.extension(x^2+x+1, 'u')
sage: F2.random_element()
(a^6 + 1)*u + a^5 + a^4 + a^3 + 1

selmer_group(S, m, proof=True)

If is an etale algebra over a number field (i.e. the coefficient ring is a number field and the modulus is squarefree), then compute the Selmer group 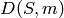, which is defined to be the subgroup of 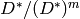consisting of elements such that is unramified at all primes of lying above a place outside of .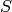

INPUT:

• S - A set of primes of the coefficient ring (which is a number field).
• m - a positive integer
• proof - if False, assume Pari’s GRH++ in computing the class group

OUTPUT:

A list of generators of .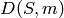

EXAMPLES:

sage: K.<a> = QuadraticField(-5)
sage: R.<x> = K[]
sage: D.<T> = R.quotient(x)
sage: D.selmer_group((), 2)
[-1, 2]
sage: D.selmer_group([K.ideal(2, -a+1)], 2)
[2, -1]
sage: D.selmer_group([K.ideal(2, -a+1), K.ideal(3, a+1)], 2)
[2, -a - 1, -1]
sage: D.selmer_group((K.ideal(2, -a+1),K.ideal(3, a+1)), 4)
[2, -a - 1, -1]
sage: D.selmer_group([K.ideal(2, -a+1)], 3)
[2]
sage: D.selmer_group([K.ideal(2, -a+1), K.ideal(3, a+1)], 3)
[2, -a - 1]
sage: D.selmer_group([K.ideal(2, -a+1), K.ideal(3, a+1), K.ideal(a)], 3)
[2, -a - 1, -a]

units(proof=True)

If this quotient ring is over a number field K, by a polynomial of nonzero discriminant, returns a list of generators of the units.

INPUT:

- ``proof`` - if False, assume Pari's GRH++ in computing the class group

OUTPUT:

A list of generators of the unit group, in the form (gen, order), where gen is a unit of order order.

EXAMPLES::

sage: K.<a> = QuadraticField(-3) sage: K.unit_group() Unit group with structure C6 of Number Field in a with defining polynomial x^2 + 3 sage: K.<a> = QQ[‘x’].quotient(x^2 + 3) sage: u = K.units()[0][0]; u -1/2*a + 1/2 sage: u^6 1 sage: u^3 -1 sage: u^2 -1/2*a - 1/2

sage: K.<a> = QuadraticField(-3)
sage: y = polygen(K)
sage: L.<b> = K['y'].quotient(y^3 + 5); L
Univariate Quotient Polynomial Ring in b over Number Field in a with defining polynomial x^2 + 3 with modulus y^3 + 5
sage: L.units()
[(-1/2*a + 1/2, 6),
 ((...1/3*a - 1)*b^2 + ...*b + ...*a + ..., +Infinity),
 ((-1/3*a + 1)*b^2 + (2/3*a - 2)*b - 5/6*a + 7/2, +Infinity)]
sage: L.<b> = K.extension(y^3 + 5)
sage: L.unit_group()
Unit group with structure C6 x Z x Z of Number Field in b with defining polynomial x^3 + 5 over its base field
sage: L.unit_group().gens()
[-1/2*a + 1/2,
 (...1/3*a - 1)*b^2 + ...*b + ...*a + ...,
 (-1/3*a + 1)*b^2 + (2/3*a - 2)*b - 5/6*a + 7/2]

Note that all the returned values live where we expect them to:

sage: L.<b> = K['y'].quotient(y^3 + 5)
sage: U = L.units()
sage: type(U[0][0])
<class 'sage.rings.polynomial.polynomial_quotient_ring_element.PolynomialQuotientRingElement'>
sage: type(U[0][1])
<type 'sage.rings.integer.Integer'>
sage: type(U[1][1])
<class 'sage.rings.infinity.PlusInfinity'>

sage.rings.polynomial.polynomial_quotient_ring.is_PolynomialQuotientRing(x)