The classes in this file are designed to be attached to p-adic parents and elements for Cython access to properties of the parent.
In addition to storing the defining polynomial (as an NTL polynomial) at different precisions, they also cache powers of p and data to speed right shifting of elements.
The hierarchy of PowComputers splits first at whether it’s for a base ring (Qp or Zp) or an extension.
Among the extension classes (those in this file), they are first split by the type of NTL polynomial (ntl_ZZ_pX or ntl_ZZ_pEX), then by the amount and style of caching (see below). Finally, there are subclasses of the ntl_ZZ_pX PowComputers that cache additional information for Eisenstein extensions.
There are three styles of caching:
- FM: caches powers of p up to the cache_limit, only caches the polynomial modulus and the ntl_ZZ_pContext of precision prec_cap.
- small: Requires cache_limit = prec_cap. Caches p^k for every k up to the cache_limit and caches a polynomial modulus and a ntl_ZZ_pContext for each such power of p.
- big: Caches as the small does up to cache_limit and caches prec_cap. Also has a dictionary that caches values above the cache_limit when they are computed (rather than at ring creation time).
AUTHORS:
Bases: sage.rings.padics.pow_computer_ext.PowComputer_ext
Returns the polynomial (with coefficient precision prec_cap) associated to this PowComputer.
The polynomial is output as an ntl_ZZ_pX.
EXAMPLES:
sage: PC = PowComputer_ext_maker(5, 5, 10, 20, False, ntl.ZZ_pX([-5,0,1],5^10), 'FM', 'e',ntl.ZZ_pX([1],5^10))
sage: PC.polynomial()
[9765620 0 1]
Runs a speed test.
INPUT:
n -- input to a function to be tested (the function needs to be set in the source code).
runs -- The number of runs of that function
OUTPUT:
The time in seconds that it takes to call the function on n, runs times.
sage: PC = PowComputer_ext_maker(5, 10, 10, 20, False, ntl.ZZ_pX([-5, 0, 1], 5^10), 'small', 'e',ntl.ZZ_pX([1],5^10))
sage: PC.speed_test(10, 10^6) # random
0.0090679999999991878
Bases: sage.rings.padics.pow_computer_ext.PowComputer_ZZ_pX
This class only caches a context and modulus for p^prec_cap.
Designed for use with fixed modulus p-adic rings, in Eisenstein
and unramified extensions of  .
.
Bases: sage.rings.padics.pow_computer_ext.PowComputer_ZZ_pX_FM
This class computes and stores low_shifter and high_shifter, which aid in right shifting elements.
Bases: sage.rings.padics.pow_computer_ext.PowComputer_ZZ_pX
This class caches all contexts and moduli between 1 and cache_limit, and also caches for prec_cap. In addition, it stores a dictionary of contexts and moduli of
Resets the dictionaries. Note that if there are elements lying around that need access to these dictionaries, calling this function and then doing arithmetic with those elements could cause trouble (if the context object gets garbage collected for example. The bugs introduced could be very subtle, because NTL will generate a new context object and use it, but there’s the potential for the object to be incompatible with the different context object).
EXAMPLES:
sage: A = PowComputer_ext_maker(5, 6, 10, 20, False, ntl.ZZ_pX([-5,0,1],5^10), 'big','e',ntl.ZZ_pX([1],5^10))
sage: P = A._get_context_test(8)
sage: A._context_dict()
{8: NTL modulus 390625}
sage: A.reset_dictionaries()
sage: A._context_dict()
{}
Bases: sage.rings.padics.pow_computer_ext.PowComputer_ZZ_pX_big
This class computes and stores low_shifter and high_shifter, which aid in right shifting elements. These are only stored at maximal precision: in order to get lower precision versions just reduce mod p^n.
Bases: sage.rings.padics.pow_computer_ext.PowComputer_ZZ_pX
This class caches contexts and moduli densely between 1 and cache_limit. It requires cache_limit == prec_cap.
It is intended for use with capped relative and capped absolute rings and fields, in Eisenstein and unramified extensions of the base p-adic fields.
Bases: sage.rings.padics.pow_computer_ext.PowComputer_ZZ_pX_small
This class computes and stores low_shifter and high_shifter, which aid in right shifting elements. These are only stored at maximal precision: in order to get lower precision versions just reduce mod p^n.
Returns a PowComputer that caches the values 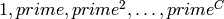 ,
where
,
where  is cache_limit.
is cache_limit.
Once you create a PowComputer, merely call it to get values out. You can input any integer, even if it’s outside of the precomputed range.
INPUT:
- prime -- An integer, the base that you want to exponentiate.
- cache_limit -- A positive integer that you want to cache
powers up to.
- prec_cap -- The cap on precisions of elements. For ramified
extensions, p^((prec_cap - 1) // e) will be the largest
power of p distinguishable from zero
- in_field -- Boolean indicating whether this PowComputer is
attached to a field or not.
- poly -- An ntl_ZZ_pX or ntl_ZZ_pEX defining the extension.
It should be defined modulo p^((prec_cap - 1) // e + 1)
- prec_type -- 'FM', 'small', or 'big', defining how caching
is done.
- ext_type -- 'u' = unramified, 'e' = Eisenstein, 't' =
two-step
- shift_seed -- (required only for Eisenstein and two-step)
For Eisenstein and two-step extensions, if f = a_n x^n - p
a_{n-1} x^{n-1} - ... - p a_0 with a_n a unit, then
shift_seed should be 1/a_n (a_{n-1} x^{n-1} + ... + a_0)
EXAMPLES:
sage: PC = PowComputer_ext_maker(5, 10, 10, 20, False, ntl.ZZ_pX([-5, 0, 1], 5^10), 'small','e',ntl.ZZ_pX([1],5^10))
sage: PC
PowComputer_ext for 5, with polynomial [9765620 0 1]
Shifts _a right _n x-adic digits, where x is considered modulo the polynomial in _shifter.
EXAMPLES:
sage: from sage.rings.padics.pow_computer_ext import ZZ_pX_eis_shift_test
sage: A = PowComputer_ext_maker(5, 3, 10, 40, False, ntl.ZZ_pX([-5,75,15,0,1],5^10), 'big', 'e',ntl.ZZ_pX([1,-15,-3],5^10))
sage: ZZ_pX_eis_shift_test(A, [0, 1], 1, 5)
[1]
sage: ZZ_pX_eis_shift_test(A, [0, 0, 1], 1, 5)
[0 1]
sage: ZZ_pX_eis_shift_test(A, [5], 1, 5)
[75 15 0 1]
sage: ZZ_pX_eis_shift_test(A, [1], 1, 5)
[]
sage: ZZ_pX_eis_shift_test(A, [17, 91, 8, -2], 1, 5)
[316 53 3123 3]
sage: ZZ_pX_eis_shift_test(A, [316, 53, 3123, 3], -1, 5)
[15 91 8 3123]
sage: ZZ_pX_eis_shift_test(A, [15, 91, 8, 3123], 1, 5)
[316 53 3123 3]