PowComputer.

A class for computing and caching powers of the same integer.

This class is designed to be used as a field of p-adic rings and fields. Since elements of p-adic rings and fields need to use powers of p over and over, this class precomputes and stores powers of p. There is no reason that the base has to be prime however.

EXAMPLES:

sage: X = PowComputer(3, 4, 10)
sage: X(3)
27
sage: X(10) == 3^10
True

AUTHORS:

• David Roe

sage.rings.padics.pow_computer.PowComputer(m, cache_limit, prec_cap, in_field=False)

Returns a PowComputer that caches the values 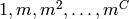, where is cache_limit.

Once you create a PowComputer, merely call it to get values out.

You can input any integer, even if it’s outside of the precomputed range.

INPUT:

* m -- An integer, the base that you want to exponentiate.
* cache_limit -- A positive integer that you want to cache powers up to.

EXAMPLES:

sage: PC = PowComputer(3, 5, 10)
sage: PC
PowComputer for 3
sage: PC(4)
81
sage: PC(6)
729
sage: PC(-1)
1/3

class sage.rings.padics.pow_computer.PowComputer_base

Bases: sage.rings.padics.pow_computer.PowComputer_class

class sage.rings.padics.pow_computer.PowComputer_class

Bases: sage.structure.sage_object.SageObject

pow_Integer_Integer(n)

Tests the pow_Integer function.

EXAMPLES:

sage: PC = PowComputer(3, 5, 10)
sage: PC.pow_Integer_Integer(4)
81
sage: PC.pow_Integer_Integer(6)
729
sage: PC.pow_Integer_Integer(0)
1
sage: PC.pow_Integer_Integer(10)
59049
sage: PC = PowComputer_ext_maker(3, 5, 10, 20, False, ntl.ZZ_pX([-3,0,1], 3^10), 'big','e',ntl.ZZ_pX([1],3^10))
sage: PC.pow_Integer_Integer(4)
81
sage: PC.pow_Integer_Integer(6)
729
sage: PC.pow_Integer_Integer(0)
1
sage: PC.pow_Integer_Integer(10)
59049

sage.rings.padics.pow_computer.clear_mpz_globals()

sage.rings.padics.pow_computer.gmp_randrange(n1, n2)

sage.rings.padics.pow_computer.init_mpz_globals()