Elements of p-Adic Rings with Fixed Modulus
AUTHORS:
Unpickles a capped relative element.
EXAMPLES:
sage: from sage.rings.padics.padic_fixed_mod_element import make_pAdicFixedModElement
sage: R = ZpFM(5)
sage: a = make_pAdicFixedModElement(R, 17*25); a
2*5^2 + 3*5^3 + O(5^20)
Bases: sage.rings.padics.padic_base_generic_element.pAdicBaseGenericElement
Returns a new element truncated modulo p^absprec.
INPUT:
- self -- a p-adic element
- absprec -- an integer
OUTPUT:
- element -- a new element truncated modulo p^absprec.
EXAMPLES:
sage: R = Zp(7,4,'fixed-mod','series'); a = R(8); a.add_bigoh(1)
1 + O(7^4)
Returns whether self is equal to right modulo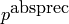 
.
If absprec is None, returns if self == 0.
INPUT:
- self -- a p-adic element
- right -- a p-addic element with the same parent
- absprec -- a positive integer (or None)
OUTPUT:
boolean -- whether self is equal to right
EXAMPLES:
sage: R = ZpFM(2, 6)
sage: R(13).is_equal_to(R(13))
True
sage: R(13).is_equal_to(R(13+2^10))
True
sage: R(13).is_equal_to(R(17), 2)
True
sage: R(13).is_equal_to(R(17), 5)
False
Returns whether self is zero modulo .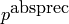
INPUT:
- self -- a p-adic element
- absprec -- an integer
OUTPUT:
boolean -- whether self is zero
EXAMPLES:
sage: R = ZpFM(17, 6)
sage: R(0).is_zero()
True
sage: R(17^6).is_zero()
True
sage: R(17^2).is_zero(absprec=2)
True
Return an integer congruent to self modulo self’s precision.
INPUT:
- self -- a p-adic element
OUTPUT:
- integer -- a integer congruent to self mod $p^{\mbox{prec}}$
EXAMPLES:
sage: R = Zp(7,4,'fixed-mod'); a = R(8); a.lift()
8
sage: type(a.lift())
<type 'sage.rings.integer.Integer'>
Returns self.
For compatibility with other p-adic types.
EXAMPLES:
sage: R = ZpFM(5); a = R(5); a.lift_to_precision(7)
5 + O(5^20)
Returns a list of coefficients of p starting with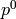 
.
INPUT:
- self -- a p-adic element
- lift_mode -- 'simple', 'smallest' or 'teichmuller' (default 'simple')
OUTPUT:
- list -- the list of coefficients of self
NOTES:
Returns a list [a_0, a_1, \ldots, a_n] so that each a_i is an integer
and \sum_{i = 0}^n a_i * p^i = self, modulo the precision cap.
If lift_mode = 'simple', 0 <= a_i < p.
If lift_mode = 'smallest', -p/2 < a_i <= p/2.
If lift_mode = 'teichmuller', a_i^p = a_i, modulo the precision cap.
EXAMPLES:
sage: R = ZpFM(7,6); a = R(12837162817); a
3 + 4*7 + 4*7^2 + 4*7^4 + O(7^6)
sage: L = a.list(); L
[3, 4, 4, 0, 4]
sage: sum([L[i] * 7^i for i in range(len(L))]) == a
True
sage: L = a.list('smallest'); L
[3, -3, -2, 1, -3, 1]
sage: sum([L[i] * 7^i for i in range(len(L))]) == a
True
sage: L = a.list('teichmuller'); L
[3 + 4*7 + 6*7^2 + 3*7^3 + 2*7^5 + O(7^6),
O(7^6),
5 + 2*7 + 3*7^3 + 6*7^4 + 4*7^5 + O(7^6),
1 + O(7^6),
3 + 4*7 + 6*7^2 + 3*7^3 + 2*7^5 + O(7^6),
5 + 2*7 + 3*7^3 + 6*7^4 + 4*7^5 + O(7^6)]
sage: sum([L[i] * 7^i for i in range(len(L))])
3 + 4*7 + 4*7^2 + 4*7^4 + O(7^6)
Returns the minimum possible multiplicative order of self.
INPUT:
- self -- a p-adic element
OUTPUT:
- integer -- the multiplicative order of self. This is
the minimum multiplicative order of all elements of Z_p
lifting self to infinite precision.
EXAMPLES:
sage: R = ZpFM(7, 6)
sage: R(1/3)
5 + 4*7 + 4*7^2 + 4*7^3 + 4*7^4 + 4*7^5 + O(7^6)
sage: R(1/3).multiplicative_order()
+Infinity
sage: R(7).multiplicative_order()
+Infinity
sage: R(1).multiplicative_order()
1
sage: R(-1).multiplicative_order()
2
sage: R.teichmuller(3).multiplicative_order()
6
Returns a list of coefficients of p starting with 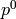up to
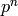exclusive (padded with zeros if needed)
INPUT:
- self -- a p-adic element
- n -- an integer
OUTPUT:
- list -- the list of coefficients of self
EXAMPLES:
sage: R = Zp(7,4,'fixed-mod'); a = R(2*7+7**2); a.padded_list(5)
[0, 2, 1, 0, 0]
NOTE:
For elements with positive valuation, this function will
return a list with leading 0s, unlike for field elements.
The slice operators throw an error if asked for a slice
above the precision, while this function works
Returns the absolute precision of self.
INPUT:
- self -- a p-adic element
OUTPUT:
- integer -- the absolute precision of self
EXAMPLES:
sage: R = Zp(7,4,'fixed-mod'); a = R(7); a.precision_absolute()
4
Returns the relative precision of self
INPUT:
- self -- a p-adic element
OUTPUT:
- integer -- the relative precision of self
EXAMPLES:
sage: R = Zp(7,4,'fixed-mod'); a = R(7); a.precision_relative()
3
sage: a = R(0); a.precision_relative()
0
Reduces this mod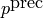 
INPUT:
- self -- a p-adic element
- absprec - an integer (default 1)
OUTPUT:
- element of Z/(p^prec Z) -- self reduced mod p^prec
EXAMPLES:
sage: R = Zp(7,4,'fixed-mod'); a = R(8); a.residue(1)
1
Returns the unit part of self.
If the valuation of self is positive, then the high digits of the result will be zero.
INPUT:
- self -- a p-adic element
OUTPUT:
- p-adic element -- the unit part of self
EXAMPLES:
sage: R = Zp(17, 4, 'fixed-mod')
sage: R(5).unit_part()
5 + O(17^4)
sage: R(18*17).unit_part()
1 + 17 + O(17^4)
sage: R(0).unit_part()
O(17^4)
sage: type(R(5).unit_part())
<type 'sage.rings.padics.padic_fixed_mod_element.pAdicFixedModElement'>
sage: R = ZpFM(5, 5); a = R(75); a.unit_part()
3 + O(5^5)
Returns a 2-tuple, the first element set to the valuation of self, and the second to the unit part of self.
If self == 0, then the unit part is O(p^self.parent().precision_cap()).
EXAMPLES:
sage: R = ZpFM(5,5)
sage: a = R(75); b = a - a
sage: a.val_unit()
(2, 3 + O(5^5))
sage: b.val_unit()
(5, O(5^5))
Returns the valuation of self.
If self is zero, the valuation returned is the precision of the ring.
INPUT:
- self -- a p-adic element
OUTPUT:
- integer -- the valuation of self.
EXAMPLES:
sage: R = Zp(17, 4,'fixed-mod')
sage: a = R(2*17^2)
sage: a.valuation()
2
sage: R = Zp(5, 4,'fixed-mod')
sage: R(0).valuation()
4
sage: R(1).valuation()
0
sage: R(2).valuation()
0
sage: R(5).valuation()
1
sage: R(10).valuation()
1
sage: R(25).valuation()
2
sage: R(50).valuation()
2
-Adic Capped Absolute Element.