 -Adic Base Generic Element.¶
-Adic Base Generic Element.¶A common superclass for features shared among all elements of  and
and
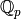 (regardless of implementation).
(regardless of implementation).
AUTHORS:
Bases: sage.rings.padics.padic_generic_element.pAdicGenericElement
Returns the  -adic absolute value of self.
-adic absolute value of self.
This is normalized so that the absolute value of  is
is 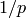 .
.
INPUT:
EXAMPLES: sage: a = Qp(5)(15); a.abs() 1/5 sage: a.abs(53) 0.200000000000000
Compute the  -adic exponential of any element of
-adic exponential of any element of
 where the series converges.
where the series converges.
EXAMPLES:
Borrowed from log.:
sage: Z13 = Zp(13, 10, print_mode='series')
sage: a = Z13(13 + 6*13**2 + 2*13**3 + 5*13**4 + 10*13**6 + 13**7 + 11*13**8 + 8*13**9).add_bigoh(10); a
13 + 6*13^2 + 2*13^3 + 5*13^4 + 10*13^6 + 13^7 + 11*13^8 + 8*13^9 + O(13^10)
sage: a.exp()
1 + 13 + O(13^10)
sage: Q13 = Qp(13, 10, print_mode='series')
sage: a = Q13(13 + 6*13**2 + 2*13**3 + 5*13**4 + 10*13**6 + 13**7 + 11*13**8 + 8*13**9).add_bigoh(10); a
13 + 6*13^2 + 2*13^3 + 5*13^4 + 10*13^6 + 13^7 + 11*13^8 + 8*13^9 + O(13^10)
sage: a.exp()
1 + 13 + O(13^10)
The next few examples illustrate precision when computing
 -adic exps. First we create a field with emph{default}
precision 10.:
-adic exps. First we create a field with emph{default}
precision 10.:
sage: R = Zp(5,10, print_mode='series')
sage: e = R(2*5 + 2*5**2 + 4*5**3 + 3*5**4 + 5**5 + 3*5**7 + 2*5**8 + 4*5**9).add_bigoh(10); e
2*5 + 2*5^2 + 4*5^3 + 3*5^4 + 5^5 + 3*5^7 + 2*5^8 + 4*5^9 + O(5^10)
sage: e.exp()*R.teichmuller(4)
4 + 2*5 + 3*5^3 + O(5^10)
sage: K = Qp(5,10, print_mode='series')
sage: e = K(2*5 + 2*5**2 + 4*5**3 + 3*5**4 + 5**5 + 3*5**7 + 2*5**8 + 4*5**9).add_bigoh(10); e
2*5 + 2*5^2 + 4*5^3 + 3*5^4 + 5^5 + 3*5^7 + 2*5^8 + 4*5^9 + O(5^10)
sage: e.exp()*K.teichmuller(4)
4 + 2*5 + 3*5^3 + O(5^10)
TESTS:
Check that results are consistent over a range of precision:
sage: max_prec = 40
sage: p = 3
sage: K = Zp(p, max_prec)
sage: full_exp = (K(p)).exp()
sage: for prec in range(2, max_prec):
... ll = (K(p).add_bigoh(prec)).exp()
... assert ll == full_exp
... assert ll.precision_absolute() == prec
sage: K = Qp(p, max_prec)
sage: full_exp = (K(p)).exp()
sage: for prec in range(2, max_prec):
... ll = (K(p).add_bigoh(prec)).exp()
... assert ll == full_exp
... assert ll.precision_absolute() == prec
AUTHORS:
Compute the  -adic logarithm of any unit in
-adic logarithm of any unit in  .
(See below for normalization.)
.
(See below for normalization.)
The usual power series for log with values in the additive
group of  only converges for 1-units (units
congruent to 1 modulo
only converges for 1-units (units
congruent to 1 modulo  ). However, there is a unique
extension of log to a homomorphism defined on all the units.
If
). However, there is a unique
extension of log to a homomorphism defined on all the units.
If 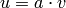 is a unit with
is a unit with 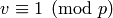 and
and
 a Teichmuller representative, then we define
a Teichmuller representative, then we define 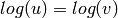 . This is the correct extension because the units
. This is the correct extension because the units 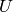 of
of  split as a product
split as a product 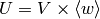 , where
, where 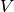 is the subgroup of 1-units and
is the subgroup of 1-units and  is a
is a
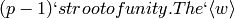 factor is
torsion, so must go to 0 under any homomorphism to the torsion
free group
factor is
torsion, so must go to 0 under any homomorphism to the torsion
free group 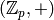 .
.
INPUTS:
 -adic element.
-adic element.NOTES:
What some other systems do:
ALGORITHM:
Input: Some p-adic unit  (or non-unit if branch is
specified).
(or non-unit if branch is
specified).
 -adic number is really a unit
(i.e., valuation 0), or take the unit part and multiply by
branch * self.valuation() if not and branch
specified.
-adic number is really a unit
(i.e., valuation 0), or take the unit part and multiply by
branch * self.valuation() if not and branch
specified.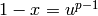 , which is a 1-unit.
, which is a 1-unit...math
\log(1-x) = F(x) = -x - 1/2*x^2 - 1/3*x^3 - 1/4*x^4 - 1/5*x^5 - \cdots
to compute the logarithm 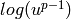 . Use enough terms so
that terms added on are zero
. Use enough terms so
that terms added on are zero
..math
\log(u) = \log(u^{p-1})/(p-1) = F(1-u^{p-1})/(p-1).
EXAMPLES:
sage: Z13 = Zp(13, 10, print_mode='series')
sage: a = Z13(14); a
1 + 13 + O(13^10)
Note that the relative precision decreases when we take log: it is the absolute precision that is preserved.:
sage: a.log()
13 + 6*13^2 + 2*13^3 + 5*13^4 + 10*13^6 + 13^7 + 11*13^8 + 8*13^9 + O(13^10)
sage: Q13 = Qp(13, 10, print_mode='series')
sage: a = Q13(14); a
1 + 13 + O(13^10)
sage: a.log()
13 + 6*13^2 + 2*13^3 + 5*13^4 + 10*13^6 + 13^7 + 11*13^8 + 8*13^9 + O(13^10)
The next few examples illustrate precision when computing
 -adic logs. First we create a field with emph{default}
precision 10.:
-adic logs. First we create a field with emph{default}
precision 10.:
sage: R = Zp(5,10, print_mode='series')
sage: e = R(389); e
4 + 2*5 + 3*5^3 + O(5^10)
sage: e.log()
2*5 + 2*5^2 + 4*5^3 + 3*5^4 + 5^5 + 3*5^7 + 2*5^8 + 4*5^9 + O(5^10)
sage: K = Qp(5,10, print_mode='series')
sage: e = K(389); e
4 + 2*5 + 3*5^3 + O(5^10)
sage: e.log()
2*5 + 2*5^2 + 4*5^3 + 3*5^4 + 5^5 + 3*5^7 + 2*5^8 + 4*5^9 + O(5^10)
Check that results are consistent over a range of precision:
sage: max_prec = 40
sage: p = 3
sage: K = Zp(p, max_prec)
sage: full_log = (K(1 + p)).log()
sage: for prec in range(2, max_prec):
... ll = (K(1 + p).add_bigoh(prec)).log()
... assert ll == full_log
... assert ll.precision_absolute() == prec
AUTHORS:
TODO:
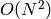 . This can be improved to
soft-
. This can be improved to
soft-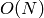 using algorithm described by Dan Bernstein:
http://cr.yp.to/lineartime/multapps-20041007.pdf
using algorithm described by Dan Bernstein:
http://cr.yp.to/lineartime/multapps-20041007.pdfReturns a minimal polynomial of this  -adic element, i.e., x - self
-adic element, i.e., x - self
INPUT:
 -adic element
-adic elementOUTPUT:
 -adic element,
i.e., x - self
-adic element,
i.e., x - selfEXAMPLES:
sage: Zp(5,5)(1/3).minimal_polynomial('x')
(1 + O(5^5))*x + (3 + 5 + 3*5^2 + 5^3 + 3*5^4 + O(5^5))
Returns the norm of this  -adic element over the ground ring.
-adic element over the ground ring.
NOTE! This is not the  -adic absolute value. This is a field
theoretic norm down to a ground ring. If you want the
-adic absolute value. This is a field
theoretic norm down to a ground ring. If you want the  -adic
absolute value, use the abs() function instead.
-adic
absolute value, use the abs() function instead.
INPUT:
 -adic element
-adic elementOUTPUT:
 -adic element over the ground
ring
-adic element over the ground
ringEXAMPLES:
sage: Zp(5)(5).norm()
5 + O(5^21)
Returns the trace of this  -adic element over the ground ring
-adic element over the ground ring
INPUT:
 -adic element
-adic elementOUTPUT:
 -adic element over the
ground ring
-adic element over the
ground ringEXAMPLES:
sage: Zp(5,5)(5).trace()
5 + O(5^6)