p-Adic Capped Relative Element.

Elements of p-Adic Rings with Capped Relative Precision

AUTHORS:

• David Roe
• Genya Zaytman: documentation
• David Harvey: doctests

TESTS:

sage: M = MatrixSpace(pAdicField(3,100),2)
sage: (M([1,0,0,90]) - (1+O(3^100)) * M(1)).left_kernel()
Vector space of degree 2 and dimension 1 over 3-adic Field with capped relative precision 100
Basis matrix:
[1 + O(3^100)            0]

sage.rings.padics.padic_capped_relative_element.clear_mpz_globals()

sage.rings.padics.padic_capped_relative_element.gmp_randrange(n1, n2)

sage.rings.padics.padic_capped_relative_element.init_mpz_globals()

class sage.rings.padics.padic_capped_relative_element.pAdicCappedRelativeElement

Bases: sage.rings.padics.padic_base_generic_element.pAdicBaseGenericElement

add_bigoh(absprec)

Returns a new element with absolute precision decreased to absprec.

INPUT:

self -- a p-adic element
absprec -- an integer

OUTPUT:

element -- self with precision set to the minimum of
           self's precision and absprec

EXAMPLE:

sage: R = Zp(7,4,'capped-rel','series'); a = R(8); a.add_bigoh(1)
1 + O(7)
sage: b = R(0); b.add_bigoh(3)
O(7^3)
sage: R = Qp(7,4); a = R(8); a.add_bigoh(1)
1 + O(7)
sage: b = R(0); b.add_bigoh(3)
O(7^3)

The precision never increases::

sage: R(4).add_bigoh(2).add_bigoh(4)
4 + O(7^2)

Another example that illustrates that the precision does
not increase::

sage: k = Qp(3,5)
sage: a = k(1234123412/3^70); a
2*3^-70 + 3^-69 + 3^-68 + 3^-67 + O(3^-65)
sage: a.add_bigoh(2)
2*3^-70 + 3^-69 + 3^-68 + 3^-67 + O(3^-65)

sage: k = Qp(5,10)
sage: a = k(1/5^3 + 5^2); a
5^-3 + 5^2 + O(5^7)
sage: a.add_bigoh(2)
5^-3 + O(5^2)
sage: a.add_bigoh(-1)
5^-3 + O(5^-1)            

is_equal_to(right, absprec=None)

Returns whether self is equal to right modulo .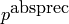

if absprec is None, returns True if self and right are equal to the minimum of their precisions.

INPUT:

• self – a p-adic element
• right – a p-addic element
• absprec – an integer or None

OUTPUT:

• boolean – whether self is equal to right (modulo )

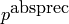EXAMPLES:

sage: R = Zp(5, 10); a = R(0); b = R(0, 3); c = R(75, 5)
sage: aa = a + 625; bb = b + 625; cc = c + 625
sage: a.is_equal_to(aa), a.is_equal_to(aa, 4), a.is_equal_to(aa, 5)
(False, True, False)
sage: a.is_equal_to(aa, 15)
...
PrecisionError: Elements not known to enough precision

sage: a.is_equal_to(a, 50000)
True

sage: a.is_equal_to(b), a.is_equal_to(b, 2)
(True, True)
sage: a.is_equal_to(b, 5)
...
PrecisionError: Elements not known to enough precision

sage: b.is_equal_to(b, 5)
...
PrecisionError: Elements not known to enough precision

sage: b.is_equal_to(bb, 3)
True
sage: b.is_equal_to(bb, 4)
...
PrecisionError: Elements not known to enough precision

sage: c.is_equal_to(b, 2), c.is_equal_to(b, 3)
(True, False)
sage: c.is_equal_to(b, 4)
...
PrecisionError: Elements not known to enough precision

sage: c.is_equal_to(cc, 2), c.is_equal_to(cc, 4), c.is_equal_to(cc, 5)
(True, True, False)

TESTS:

sage: aa.is_equal_to(a), aa.is_equal_to(a, 4), aa.is_equal_to(a, 5)
(False, True, False)
sage: aa.is_equal_to(a, 15)
...
PrecisionError: Elements not known to enough precision

sage: b.is_equal_to(a), b.is_equal_to(a, 2)
(True, True)
sage: b.is_equal_to(a, 5)
...
PrecisionError: Elements not known to enough precision

sage: bb.is_equal_to(b, 3)
True
sage: bb.is_equal_to(b, 4)
...
PrecisionError: Elements not known to enough precision

sage: b.is_equal_to(c, 2), b.is_equal_to(c, 3)
(True, False)
sage: b.is_equal_to(c, 4)
...
PrecisionError: Elements not known to enough precision

sage: cc.is_equal_to(c, 2), cc.is_equal_to(c, 4), cc.is_equal_to(c, 5)
(True, True, False)

is_zero(absprec=None)

Returns whether self is zero modulo .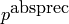

If absprec is None, returns True if this element is indistinguishable from zero.

INPUT:

- self -- a p-adic element
- absprec -- an integer or None

OUTPUT:

- boolean -- whether self is zero

EXAMPLES:

sage: R = Zp(5); a = R(0); b = R(0,5); c = R(75)
sage: a.is_zero(), a.is_zero(6)
(True, True)
sage: b.is_zero(), b.is_zero(5)
(True, True)
sage: c.is_zero(), c.is_zero(2), c.is_zero(3)
(False, True, False)
sage: b.is_zero(6)
...
PrecisionError: Not enough precision to determine if element is zero

lift()

Return an integer or rational congruent to self modulo self’s precision. If a rational is returned, its denominator will eqaul p^ordp(self).

INPUT:

- self -- a p-adic element

OUTPUT:

- integer -- a integer congruent to self mod $p^{\mbox{prec}}$

EXAMPLES:

sage: R = Zp(7,4,'capped-rel'); a = R(8); a.lift()
8
sage: R = Qp(7,4); a = R(8); a.lift()
8
sage: R = Qp(7,4); a = R(8/7); a.lift()
8/7

lift_to_precision(absprec)

Returns another element of the same parent, with absolute precision at least absprec, congruent to self modulo self’s precision.

If such lifting would yield an element with precision greater than allowed by the precision cap of self’s parent, an error is raised.

EXAMPLES:

sage: R = Zp(5); a = R(0); b = R(0,5); c = R(17,3)
sage: a.lift_to_precision(5)
0
sage: b.lift_to_precision(4)
O(5^5)
sage: b.lift_to_precision(8)
O(5^8)
sage: b.lift_to_precision(40)
O(5^40)
sage: c.lift_to_precision(1)
2 + 3*5 + O(5^3)
sage: c.lift_to_precision(8)
2 + 3*5 + O(5^8)
sage: c.lift_to_precision(40)
...
PrecisionError: Precision higher than allowed by the precision cap.

list(lift_mode='simple')

Returns a list of coefficients in a power series expansion of self in terms of p. If self is a field element, they start at p^valuation, if a ring element at p^0.

INPUT:

- self -- a p-adic element
- lift_mode - 'simple', 'smallest' or 'teichmuller'

OUTPUT:

- list -- the list of coefficients of self.  These will be integers if lift_mode is 'simple' or 'smallest', and elements of self.parent() if lift_mode is 'teichmuller'

EXAMPLES:

sage: R = Zp(7,6); a = R(12837162817); a
3 + 4*7 + 4*7^2 + 4*7^4 + O(7^6)
sage: L = a.list(); L
[3, 4, 4, 0, 4]
sage: sum([L[i] * 7^i for i in range(len(L))]) == a
True
sage: L = a.list('smallest'); L
[3, -3, -2, 1, -3, 1]
sage: sum([L[i] * 7^i for i in range(len(L))]) == a
True
sage: L = a.list('teichmuller'); L
[3 + 4*7 + 6*7^2 + 3*7^3 + 2*7^5 + O(7^6),
0,
5 + 2*7 + 3*7^3 + O(7^4),
1 + O(7^3),
3 + 4*7 + O(7^2),
5 + O(7)]
sage: sum([L[i] * 7^i for i in range(len(L))])
3 + 4*7 + 4*7^2 + 4*7^4 + O(7^6)

sage: R = Qp(7,4); a = R(6*7+7**2); a.list()
[6, 1]
sage: a.list('smallest')
[-1, 2]
sage: a.list('teichmuller')
[6 + 6*7 + 6*7^2 + 6*7^3 + O(7^4),
2 + 4*7 + 6*7^2 + O(7^3),
3 + 4*7 + O(7^2),
3 + O(7)]

NOTE:

use slice operators to get a particular range

padded_list(n, lift_mode='simple')

Returns a list of coefficients of p starting with 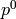up to 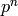exclusive (padded with zeros if needed). If a field element, starts at p^val instead.

INPUT:

self -- a p-adic element
n - an integer
lift_mode - 'simple', 'smallest' or 'teichmuller'

OUTPUT:

list -- the list of coefficients of self

EXAMPLES:

sage: R = Zp(7,3,'capped-rel'); a = R(2*7+7**2); a.padded_list(5)
[0, 2, 1, 0, 0]
sage: R = Qp(7,3); a = R(2*7+7**2); a.padded_list(5)
[2, 1, 0, 0]
sage: a.padded_list(3)
[2, 1]

NOTE:

the slice operators throw an error if asked for a slice above the precision

precision_absolute()

Returns the absolute precision of self.

This is the power of the maximal ideal modulo which this element is defined.

INPUT:

self -- a p-adic element

OUTPUT:

integer -- the absolute precision of self

EXAMPLES:

sage: R = Zp(7,3,'capped-rel'); a = R(7); a.precision_absolute()
4
sage: R = Qp(7,3); a = R(7); a.precision_absolute()
4
sage: R(7^-3).precision_absolute()
0

precision_relative()

Returns the relative precision of self.

This is the power of the maximal ideal modulo which the unit part of self is defined.

INPUT:

self – a p-adic element

OUTPUT:

integer – the relative precision of self

EXAMPLES:

sage: R = Zp(7,3,’capped-rel’); a = R(7); a.precision_relative() 3 sage: R = Qp(7,3); a = R(7); a.precision_relative() 3 sage: a = R(7^-2, -1); a.precision_relative() 1 sage: a 7^-2 + O(7^-1)

residue(absprec=1)

Reduces this element modulo .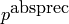

INPUT:

- self -- a p-adic element
- absprec - an integer (defaults to 1)

OUTPUT:

- element of $Z/(p^{absprec} Z)$ -- self reduced mod p^absprec

EXAMPLES:

sage: R = Zp(7,4,'capped-rel'); a = R(8); a.residue(1)
1
sage: R = Qp(7,4,'capped-rel'); a = R(8); a.residue(1)
1
sage: a.residue(6)
...
PrecisionError: Not enough precision known in order to compute residue.
sage: b = a/7
sage: b.residue(1)
...
ValueError: Element must have non-negative valuation in order to compute residue.

unit_part()

Returns the unit part of self.

INPUT:

- self -- a p-adic element

OUTPUT:

- p-adic element -- the unit part of self

EXAMPLES:

sage: R = Zp(17,4,'capped-rel')
sage: a = R(18*17)
sage: a.unit_part()
1 + 17 + O(17^4)
sage: type(a)
<type 'sage.rings.padics.padic_capped_relative_element.pAdicCappedRelativeElement'>
sage: R = Qp(17,4,'capped-rel')
sage: a = R(18*17)
sage: a.unit_part()
1 + 17 + O(17^4)
sage: type(a)
<type 'sage.rings.padics.padic_capped_relative_element.pAdicCappedRelativeElement'>
sage: a = R(2*17^2); a
2*17^2 + O(17^6)
sage: a.unit_part()
2 + O(17^4)
sage: b=1/a; b
9*17^-2 + 8*17^-1 + 8 + 8*17 + O(17^2)
sage: b.unit_part()
9 + 8*17 + 8*17^2 + 8*17^3 + O(17^4)        
sage: Zp(5)(75).unit_part()
3 + O(5^20)

val_unit()

Returns a pair (self.valuation(), self.unit_part()).

EXAMPLES:

sage: R = Zp(5); a = R(75, 20); a
3*5^2 + O(5^20)
sage: a.val_unit()
(2, 3 + O(5^18))
sage: R(0).val_unit()
(+Infinity, O(5^0))
sage: R(0, 10).val_unit()
(10, O(5^0))

sage.rings.padics.padic_capped_relative_element.unpickle_pcre_v1(R, unit, ordp, relprec)

Unpickles a capped relative element.

EXAMPLES:

sage: from sage.rings.padics.padic_capped_relative_element import unpickle_pcre_v1
sage: R = Zp(5)
sage: a = unpickle_pcre_v1(R, 17, 2, 5); a
2*5^2 + 3*5^3 + O(5^7)