 -Adic ZZ_pX CR Element.¶
-Adic ZZ_pX CR Element.¶This file implements elements of Eisenstein and unramified extensions
of  and
and 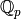 with capped relative precision.
with capped relative precision.
For the parent class see padic_extension_leaves.pyx.
The underlying implementation is through NTL’s ZZ_pX class. Each element contains the following data:
 , for Eisenstein
extensions it is not. A value equal to the maximum value of a long
indicates that the element is an exact zero.
, for Eisenstein
extensions it is not. A value equal to the maximum value of a long
indicates that the element is an exact zero. , in
the case of unramified extensions that there is at least one
coefficient that is not divisible by
, in
the case of unramified extensions that there is at least one
coefficient that is not divisible by  ). A negative value
indicates that the element may or may not be normalized. A zero
value indicates that the element is zero to some precision. If so,
ordp gives the absolute precision of the element. If ordp
is greater than maxordp, then the element is an exact zero.
). A negative value
indicates that the element may or may not be normalized. A zero
value indicates that the element is zero to some precision. If so,
ordp gives the absolute precision of the element. If ordp
is greater than maxordp, then the element is an exact zero. is the uniformizer in the case of Eisenstein
extensions. If the element is not normalized, the unit may or
may not actually be a unit. This ZZ_pX is created with global
ntl modulus determined by the absolute value of relprec. If
relprec is 0, unit is not initialized, or destructed if
normalized and found to be zero. Otherwise, let
is the uniformizer in the case of Eisenstein
extensions. If the element is not normalized, the unit may or
may not actually be a unit. This ZZ_pX is created with global
ntl modulus determined by the absolute value of relprec. If
relprec is 0, unit is not initialized, or destructed if
normalized and found to be zero. Otherwise, let  be relprec and
be relprec and
 be the ramification index over
be the ramification index over 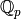 or
or  .
Then the modulus of unit is given by
.
Then the modulus of unit is given by 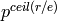 . Note that all
kinds of problems arise if you try to mix moduli.
ZZ_pX_conv_modulus gives a semi-safe way to convert between
different moduli without having to pass through ZZX (see
sage/libs/ntl/decl.pxi and c_lib/src/ntl_wrap.cpp)
. Note that all
kinds of problems arise if you try to mix moduli.
ZZ_pX_conv_modulus gives a semi-safe way to convert between
different moduli without having to pass through ZZX (see
sage/libs/ntl/decl.pxi and c_lib/src/ntl_wrap.cpp) that
is indistinguishable from zero.
that
is indistinguishable from zero. . The first two return pointers. See
sage/rings/padics/pow_computer_ext for examples and important
warnings.
. The first two return pointers. See
sage/rings/padics/pow_computer_ext for examples and important
warnings.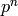 . The capdiv
version divides by prime_pow.e as appropriate.
top_context corresponds to
. The capdiv
version divides by prime_pow.e as appropriate.
top_context corresponds to 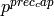 .
.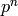 (appropriately divided
by prime_pow.e in the capdiv case).
(appropriately divided
by prime_pow.e in the capdiv case).EXAMPLES:
An Eisenstein extension:
sage: R = Zp(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f); W
Eisenstein Extension of 5-adic Ring with capped relative precision 5 in w defined by (1 + O(5^5))*x^5 + (O(5^6))*x^4 + (3*5^2 + O(5^6))*x^3 + (2*5 + 4*5^2 + 4*5^3 + 4*5^4 + 4*5^5 + O(5^6))*x^2 + (5^3 + O(5^6))*x + (4*5 + 4*5^2 + 4*5^3 + 4*5^4 + 4*5^5 + O(5^6))
sage: z = (1+w)^5; z
1 + w^5 + w^6 + 2*w^7 + 4*w^8 + 3*w^10 + w^12 + 4*w^13 + 4*w^14 + 4*w^15 + 4*w^16 + 4*w^17 + 4*w^20 + w^21 + 4*w^24 + O(w^25)
sage: y = z >> 1; y
w^4 + w^5 + 2*w^6 + 4*w^7 + 3*w^9 + w^11 + 4*w^12 + 4*w^13 + 4*w^14 + 4*w^15 + 4*w^16 + 4*w^19 + w^20 + 4*w^23 + O(w^24)
sage: y.valuation()
4
sage: y.precision_relative()
20
sage: y.precision_absolute()
24
sage: z - (y << 1)
1 + O(w^25)
sage: (1/w)^12+w
w^-12 + w + O(w^13)
sage: (1/w).parent()
Eisenstein Extension of 5-adic Field with capped relative precision 5 in w defined by (1 + O(5^5))*x^5 + (O(5^6))*x^4 + (3*5^2 + O(5^6))*x^3 + (2*5 + 4*5^2 + 4*5^3 + 4*5^4 + 4*5^5 + O(5^6))*x^2 + (5^3 + O(5^6))*x + (4*5 + 4*5^2 + 4*5^3 + 4*5^4 + 4*5^5 + O(5^6))
An unramified extension:
sage: g = x^3 + 3*x + 3
sage: A.<a> = R.ext(g)
sage: z = (1+a)^5; z
(2*a^2 + 4*a) + (3*a^2 + 3*a + 1)*5 + (4*a^2 + 3*a + 4)*5^2 + (4*a^2 + 4*a + 4)*5^3 + (4*a^2 + 4*a + 4)*5^4 + O(5^5)
sage: z - 1 - 5*a - 10*a^2 - 10*a^3 - 5*a^4 - a^5
O(5^5)
sage: y = z >> 1; y
(3*a^2 + 3*a + 1) + (4*a^2 + 3*a + 4)*5 + (4*a^2 + 4*a + 4)*5^2 + (4*a^2 + 4*a + 4)*5^3 + O(5^4)
sage: 1/a
(3*a^2 + 4) + (a^2 + 4)*5 + (3*a^2 + 4)*5^2 + (a^2 + 4)*5^3 + (3*a^2 + 4)*5^4 + O(5^5)
Different printing modes:
sage: R = Zp(5, print_mode='digits'); S.<x> = R[]; f = x^5 + 75*x^3 - 15*x^2 + 125*x -5; W.<w> = R.ext(f)
sage: z = (1+w)^5; repr(z)
'...4110403113210310442221311242000111011201102002023303214332011214403232013144001400444441030421100001'
sage: R = Zp(5, print_mode='bars'); S.<x> = R[]; g = x^3 + 3*x + 3; A.<a> = R.ext(g)
sage: z = (1+a)^5; repr(z)
'...[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 3, 4]|[1, 3, 3]|[0, 4, 2]'
sage: R = Zp(5, print_mode='terse'); S.<x> = R[]; f = x^5 + 75*x^3 - 15*x^2 + 125*x -5; W.<w> = R.ext(f)
sage: z = (1+w)^5; z
6 + 95367431640505*w + 25*w^2 + 95367431640560*w^3 + 5*w^4 + O(w^100)
sage: R = Zp(5, print_mode='val-unit'); S.<x> = R[]; f = x^5 + 75*x^3 - 15*x^2 + 125*x -5; W.<w> = R.ext(f)
sage: y = (1+w)^5 - 1; y
w^5 * (2090041 + 19073486126901*w + 1258902*w^2 + 674*w^3 + 16785*w^4) + O(w^100)
You can get at the underlying ntl unit:
sage: z._ntl_rep()
[6 95367431640505 25 95367431640560 5]
sage: y._ntl_rep()
[2090041 19073486126901 1258902 674 16785]
sage: y._ntl_rep_abs()
([5 95367431640505 25 95367431640560 5], 0)
NOTES:
If you get an error ``internal error: can't grow this
_ntl_gbigint,`` it indicates that moduli are being mixed
inappropriately somewhere. For example, when calling a function
with a ``ZZ_pX_c`` as an argument, it copies. If the modulus is not
set to the modulus of the ``ZZ_pX_c``, you can get errors.
AUTHORS:
Unpickling.
EXAMPLES:
sage: R = Zp(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: y = W(775, 19); y
w^10 + 4*w^12 + 2*w^14 + w^15 + 2*w^16 + 4*w^17 + w^18 + O(w^19)
sage: loads(dumps(y)) #indirect doctest
w^10 + 4*w^12 + 2*w^14 + w^15 + 2*w^16 + 4*w^17 + w^18 + O(w^19)
Bases: sage.rings.padics.padic_ZZ_pX_element.pAdicZZpXElement
Returns whether self is equal to right modulo self.uniformizer()^absprec.
If absprec is None, returns if self is equal to right modulo the lower of their two precisions.
EXAMPLES:
sage: R = Zp(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(47); b = W(47 + 25)
sage: a.is_equal_to(b)
False
sage: a.is_equal_to(b, 7)
True
Returns whether the valuation of self is at least absprec. If absprec is None, returns if self is indistinguishable from zero.
If self is an inexact zero of valuation less than absprec, raises a PrecisionError.
EXAMPLES:
sage: R = Zp(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: O(w^189).is_zero()
True
sage: W(0).is_zero()
True
sage: a = W(675)
sage: a.is_zero()
False
sage: a.is_zero(7)
True
sage: a.is_zero(21)
False
Returns a pAdicZZpXCRElement congruent to self but with absolute precision at least absprec. If setting absprec that high would violate the precision cap, raises a precision error. If self is an inexact zero and absprec is greater than the maximum allowed valuation, raises an error.
Note that the new digits will not necessarily be zero.
EXAMPLES:
sage: R = Zp(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(345, 17); a
4*w^5 + 3*w^7 + w^9 + 3*w^10 + 2*w^11 + 4*w^12 + w^13 + 2*w^14 + 2*w^15 + O(w^17)
sage: b = a.lift_to_precision(19); b
4*w^5 + 3*w^7 + w^9 + 3*w^10 + 2*w^11 + 4*w^12 + w^13 + 2*w^14 + 2*w^15 + w^17 + 2*w^18 + O(w^19)
sage: c = a.lift_to_precision(24); c
4*w^5 + 3*w^7 + w^9 + 3*w^10 + 2*w^11 + 4*w^12 + w^13 + 2*w^14 + 2*w^15 + w^17 + 2*w^18 + 4*w^19 + 4*w^20 + 2*w^21 + 4*w^23 + O(w^24)
sage: a._ntl_rep()
[19 35 118 60 121]
sage: b._ntl_rep()
[19 35 118 60 121]
sage: c._ntl_rep()
[19 35 118 60 121]
Returns a list giving a series representation of self.
 times polynomials in the generator
(in the unramified case).
times polynomials in the generator
(in the unramified case).![[0,p-1]](../../../_images/math/b044ef9b265492c0b5be649bca0e579813e9b875.png) .
.![[(1-p)/2, p/2]](../../../_images/math/ad3105a4d784e104d3276dba490aef03e88beb9a.png) .
.Note that zeros are truncated from the returned list if self.parent() is a field, so you must use the valuation function to fully reconstruct self.
EXAMPLES:
sage: R = Zp(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: y = W(775, 19); y
w^10 + 4*w^12 + 2*w^14 + w^15 + 2*w^16 + 4*w^17 + w^18 + O(w^19)
sage: (y>>9).list()
[0, 1, 0, 4, 0, 2, 1, 2, 4, 1]
sage: (y>>9).list('smallest')
[0, 1, 0, -1, 0, 2, 1, 2, 0, 1]
sage: w^10 - w^12 + 2*w^14 + w^15 + 2*w^16 + w^18 + O(w^19)
w^10 + 4*w^12 + 2*w^14 + w^15 + 2*w^16 + 4*w^17 + w^18 + O(w^19)
sage: g = x^3 + 3*x + 3
sage: A.<a> = R.ext(g)
sage: y = 75 + 45*a + 1200*a^2; y
4*a*5 + (3*a^2 + a + 3)*5^2 + 4*a^2*5^3 + a^2*5^4 + O(5^6)
sage: y.list()
[[], [0, 4], [3, 1, 3], [0, 0, 4], [0, 0, 1]]
sage: y.list('smallest')
[[], [0, -1], [-2, 2, -2], [1], [0, 0, 2]]
sage: 5*((-2*5 + 25) + (-1 + 2*5)*a + (-2*5 + 2*125)*a^2)
4*a*5 + (3*a^2 + a + 3)*5^2 + 4*a^2*5^3 + a^2*5^4 + O(5^6)
sage: W(0).list()
[]
sage: W(0,4).list()
[0]
sage: A(0,4).list()
[[]]
Compute the  -adic logarithm of any unit.
(See below for normalization.)
-adic logarithm of any unit.
(See below for normalization.)
INPUT:
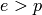 it is possible (even common) that
the image of the log map is not contained in the ring of
integers. If same_ring is True, then this function will
return a value in self.parent() or raise an error if the
answer would have negative valuation. If same_ring is
False, then this function will raise an error (this behavior
is for consistency with other
it is possible (even common) that
the image of the log map is not contained in the ring of
integers. If same_ring is True, then this function will
return a value in self.parent() or raise an error if the
answer would have negative valuation. If same_ring is
False, then this function will raise an error (this behavior
is for consistency with other  -adic types). If same_ring
is a
-adic types). If same_ring
is a  -adic field into which this fixed mod ring can be
successfully cast, then self is cast into that field and the
log is taken there. Note that this casting will assume that
self has the full precision possible.
-adic field into which this fixed mod ring can be
successfully cast, then self is cast into that field and the
log is taken there. Note that this casting will assume that
self has the full precision possible.OUTPUT:
 -adic log of self.
-adic log of self.Let  be the parent of self,
be the parent of self, 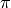 be a uniformizer of
be a uniformizer of  and
and  be
a generator for the group of roots of unity in
be
a generator for the group of roots of unity in  . The usual
power series for log with values in the additive group of
. The usual
power series for log with values in the additive group of  only converges for 1-units (units congruent to 1 modulo
only converges for 1-units (units congruent to 1 modulo 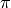 ).
However, there is a unique extension of log to a homomorphism
defined on all the units. If
).
However, there is a unique extension of log to a homomorphism
defined on all the units. If 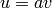 is a unit with
is a unit with 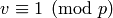 , then we define
, then we define 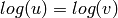 . This is the correct
extension because the units
. This is the correct
extension because the units 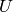 of
of  split as a product
split as a product 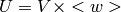 , where
, where 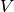 is the subgroup of 1-units. The
is the subgroup of 1-units. The 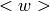 factor is
torsion, so must go to 0 under any homomorphism to the torsion
free group
factor is
torsion, so must go to 0 under any homomorphism to the torsion
free group 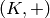 .
.
NOTES:
What some other systems do with regard to non-1-units:
In addition, if branch is specified, then the log map will work on non-units.
..math
log(pi^k \cdot u) = k \cdot branch + log(u)
ALGORITHM:
Input: Some unit u.
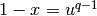 , which is a 1-unit, where
, which is a 1-unit, where  is the
order of the residue field of
is the
order of the residue field of  .
...math
\log(1-x) = F(x) = -x - 1/2*x^2 - 1/3*x^3 - 1/4*x^4 - 1/5*x^5 - \cdots
to compute the logarithm 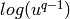 .
.
Add on terms until 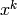 is zero modulo the precision cap, and
then determine if there are further terms that contribute to
the sum (those where
is zero modulo the precision cap, and
then determine if there are further terms that contribute to
the sum (those where  is slightly above the precision cap but
divisible by
is slightly above the precision cap but
divisible by  ).
).
..math
\log(u) = log(u^{q-1})/(q-1) = F(1-u^{q-1})/(q-1).``
EXAMPLES:
First, the Eisenstein case.:
sage: R = ZpCR(5,5)
sage: S.<x> = R[]
sage: f = x^4 + 15*x^2 + 625*x - 5
sage: W.<w> = R.ext(f)
sage: z = 1 + w^2 + 4*w^7; z
1 + w^2 + 4*w^7 + O(w^20)
Log is actually not implemented completely yet in this case!:
sage: z.log() # not tested -- what we wish would happen
4*w^2 + 3*w^4 + w^6 + w^7 + w^8 + 4*w^9 + 3*w^10 + w^12 + w^13 + 3*w^14 + w^15 + 4*w^16 + 4*w^17 + 3*w^18 + 3*w^19 + O(w^20)
sage: z.log() # what does happen
...
NotImplementedError: log is not quite working yet
Check that log is multiplicative:
sage: y = 1 + 3*w^4 + w^5
sage: y.log() + z.log() - (y*z).log() # not tested -- what we wish would happen
O(w^20)
sage: y.log() + z.log() - (y*z).log() # what does happen
...
NotImplementedError: log is not quite working yet
Now an unramified example.:
sage: g = x^3 + 3*x + 3
sage: A.<a> = R.ext(g)
sage: b = 1 + 5*(1 + a^2) + 5^3*(3 + 2*a)
sage: b.log() # not tested -- what should happen
(4*a^2 + 4)*5 + (a^2 + a + 2)*5^2 + (a^2 + 2*a + 4)*5^3 + (a^2 + 2*a + 2)*5^4 + O(5^5)
sage: b.log() # what does happen
...
NotImplementedError: log is not quite working yet
Check that log is multiplicative:
sage: c = 3 + 5^2*(2 + 4*a)
sage: b.log() + c.log() - (b*c).log() # not tested -- what should happen
O(5^5)
sage: b.log() + c.log() - (b*c).log() # what *actually* does happen
...
NotImplementedError: log is not quite working yet
AUTHORS:
TODO:
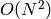 . This can be improved
to soft-
. This can be improved
to soft-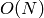 using algorithm described by Dan
Bernstein:
http://cr.yp.to/lineartime/multapps-20041007.pdf
using algorithm described by Dan
Bernstein:
http://cr.yp.to/lineartime/multapps-20041007.pdfReturns the matrix of right multiplication by the element on
the power basis 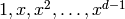 for this
extension field. Thus the rows of this matrix give the
images of each of the
for this
extension field. Thus the rows of this matrix give the
images of each of the 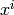 . The entries of the matrices are
IntegerMod elements, defined modulo p^(self.absprec() / e).
. The entries of the matrices are
IntegerMod elements, defined modulo p^(self.absprec() / e).
Raises an error if self has negative valuation.
EXAMPLES:
sage: R = ZpCR(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = (3+w)^7
sage: a.matrix_mod_pn()
[2757 333 1068 725 2510]
[ 50 1507 483 318 725]
[ 500 50 3007 2358 318]
[1590 1375 1695 1032 2358]
[2415 590 2370 2970 1032]
Returns the absolute precision of self, ie the power of the uniformizer modulo which this element is defined.
EXAMPLES:
sage: R = Zp(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(75, 19); a
3*w^10 + 2*w^12 + w^14 + w^16 + w^17 + 3*w^18 + O(w^19)
sage: a.valuation()
10
sage: a.precision_absolute()
19
sage: a.precision_relative()
9
sage: a.unit_part()
3 + 2*w^2 + w^4 + w^6 + w^7 + 3*w^8 + O(w^9)
sage: (a.unit_part() - 3).precision_absolute()
9
Returns the relative precision of self, ie the power of the uniformizer modulo which the unit part of self is defined.
EXAMPLES:
sage: R = Zp(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(75, 19); a
3*w^10 + 2*w^12 + w^14 + w^16 + w^17 + 3*w^18 + O(w^19)
sage: a.valuation()
10
sage: a.precision_absolute()
19
sage: a.precision_relative()
9
sage: a.unit_part()
3 + 2*w^2 + w^4 + w^6 + w^7 + 3*w^8 + O(w^9)
Returns the unit part of self, ie self / uniformizer^(self.valuation())
EXAMPLES:
sage: R = Zp(5,5)
sage: S.<x> = R[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(75, 19); a
3*w^10 + 2*w^12 + w^14 + w^16 + w^17 + 3*w^18 + O(w^19)
sage: a.valuation()
10
sage: a.precision_absolute()
19
sage: a.precision_relative()
9
sage: a.unit_part()
3 + 2*w^2 + w^4 + w^6 + w^7 + 3*w^8 + O(w^9)