 -Adic ZZ_pX CA Element.¶
-Adic ZZ_pX CA Element.¶This file implements elements of eisenstein and unramified extensions of Zp with capped absolute precision.
For the parent class see padic_extension_leaves.pyx.
The underlying implementation is through NTL’s ZZ_pX class. Each element contains the following data:
 is the uniformizer in the case of eisenstein extensions.
This ZZ_pX is created with global ntl modulus determined by absprec.
Let
is the uniformizer in the case of eisenstein extensions.
This ZZ_pX is created with global ntl modulus determined by absprec.
Let  be absprec and
be absprec and  be the ramification index over
be the ramification index over
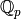 or
or  . Then the modulus is given by
. Then the modulus is given by
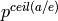 . Note that all kinds of problems arise if you try
to mix moduli. ZZ_pX_conv_modulus gives a semi-safe way to
convert between different moduli without having to pass through ZZX
(see sage/libs/ntl/decl.pxi and c_lib/src/ntl_wrap.cpp)
. Note that all kinds of problems arise if you try
to mix moduli. ZZ_pX_conv_modulus gives a semi-safe way to
convert between different moduli without having to pass through ZZX
(see sage/libs/ntl/decl.pxi and c_lib/src/ntl_wrap.cpp) that
is indistinguishable from zero.
that
is indistinguishable from zero. . The first two return pointers. See
sage/rings/padics/pow_computer_ext for examples and important
warnings.
. The first two return pointers. See
sage/rings/padics/pow_computer_ext for examples and important
warnings.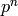 . The capdiv
version divides by prime_pow.e as appropriate.
top_context corresponds to
. The capdiv
version divides by prime_pow.e as appropriate.
top_context corresponds to 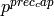 .
.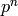 (appropriately divided
by prime_pow.e in the capdiv case).
(appropriately divided
by prime_pow.e in the capdiv case).EXAMPLES:
An eisenstein extension:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f); W
Eisenstein Extension of 5-adic Ring with capped absolute precision 5 in w defined by (1 + O(5^5))*x^5 + (3*5^2 + O(5^5))*x^3 + (2*5 + 4*5^2 + 4*5^3 + 4*5^4 + O(5^5))*x^2 + (5^3 + O(5^5))*x + (4*5 + 4*5^2 + 4*5^3 + 4*5^4 + O(5^5))
sage: z = (1+w)^5; z
1 + w^5 + w^6 + 2*w^7 + 4*w^8 + 3*w^10 + w^12 + 4*w^13 + 4*w^14 + 4*w^15 + 4*w^16 + 4*w^17 + 4*w^20 + w^21 + 4*w^24 + O(w^25)
sage: y = z >> 1; y
w^4 + w^5 + 2*w^6 + 4*w^7 + 3*w^9 + w^11 + 4*w^12 + 4*w^13 + 4*w^14 + 4*w^15 + 4*w^16 + 4*w^19 + w^20 + 4*w^23 + O(w^24)
sage: y.valuation()
4
sage: y.precision_relative()
20
sage: y.precision_absolute()
24
sage: z - (y << 1)
1 + O(w^25)
sage: (1/w)^12+w
w^-12 + w + O(w^12)
sage: (1/w).parent()
Eisenstein Extension of 5-adic Field with capped relative precision 5 in w defined by (1 + O(5^5))*x^5 + (O(5^6))*x^4 + (3*5^2 + O(5^6))*x^3 + (2*5 + 4*5^2 + 4*5^3 + 4*5^4 + 4*5^5 + O(5^6))*x^2 + (5^3 + O(5^6))*x + (4*5 + 4*5^2 + 4*5^3 + 4*5^4 + 4*5^5 + O(5^6))
An unramified extension:
sage: g = x^3 + 3*x + 3
sage: A.<a> = R.ext(g)
sage: z = (1+a)^5; z
(2*a^2 + 4*a) + (3*a^2 + 3*a + 1)*5 + (4*a^2 + 3*a + 4)*5^2 + (4*a^2 + 4*a + 4)*5^3 + (4*a^2 + 4*a + 4)*5^4 + O(5^5)
sage: z - 1 - 5*a - 10*a^2 - 10*a^3 - 5*a^4 - a^5
O(5^5)
sage: y = z >> 1; y
(3*a^2 + 3*a + 1) + (4*a^2 + 3*a + 4)*5 + (4*a^2 + 4*a + 4)*5^2 + (4*a^2 + 4*a + 4)*5^3 + O(5^4)
sage: 1/a
(3*a^2 + 4) + (a^2 + 4)*5 + (3*a^2 + 4)*5^2 + (a^2 + 4)*5^3 + (3*a^2 + 4)*5^4 + O(5^5)
Different printing modes:
sage: R = ZpCA(5, print_mode='digits'); S.<x> = ZZ[]; f = x^5 + 75*x^3 - 15*x^2 + 125*x -5; W.<w> = R.ext(f)
sage: z = (1+w)^5; repr(z)
'...4110403113210310442221311242000111011201102002023303214332011214403232013144001400444441030421100001'
sage: R = ZpCA(5, print_mode='bars'); S.<x> = ZZ[]; g = x^3 + 3*x + 3; A.<a> = R.ext(g)
sage: z = (1+a)^5; repr(z)
'...[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 4, 4]|[4, 3, 4]|[1, 3, 3]|[0, 4, 2]'
sage: R = ZpCA(5, print_mode='terse'); S.<x> = ZZ[]; f = x^5 + 75*x^3 - 15*x^2 + 125*x -5; W.<w> = R.ext(f)
sage: z = (1+w)^5; z
6 + 95367431640505*w + 25*w^2 + 95367431640560*w^3 + 5*w^4 + O(w^100)
sage: R = ZpCA(5, print_mode='val-unit'); S.<x> = ZZ[]; f = x^5 + 75*x^3 - 15*x^2 + 125*x -5; W.<w> = R.ext(f)
sage: y = (1+w)^5 - 1; y
w^5 * (2090041 + 19073486126901*w + 1258902*w^2 + 674*w^3 + 16785*w^4) + O(w^100)
You can get at the underlying ntl representation:
sage: z._ntl_rep()
[6 95367431640505 25 95367431640560 5]
sage: y._ntl_rep()
[5 95367431640505 25 95367431640560 5]
sage: y._ntl_rep_abs()
([5 95367431640505 25 95367431640560 5], 0)
NOTES:
If you get an error 'internal error: can't grow this
_ntl_gbigint,' it indicates that moduli are being mixed
inappropriately somewhere.
For example, when calling a function with a ZZ_pX_c as an
argument, it copies. If the modulus is not set to the modulus of
the ZZ_pX_c, you can get errors.
AUTHORS:
For pickling. Makes a pAdicZZpXCAElement with given parent, value, absprec.
EXAMPLES:
sage: from sage.rings.padics.padic_ZZ_pX_CA_element import make_ZZpXCAElement
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: make_ZZpXCAElement(W, ntl.ZZ_pX([3,2,4],5^3),13,0)
3 + 2*w + 4*w^2 + O(w^13)
Bases: sage.rings.padics.padic_ZZ_pX_element.pAdicZZpXElement
Returns whether self is equal to right modulo self.uniformizer()^absprec.
If absprec is None, returns if self is equal to right modulo the lower of their two precisions.
EXAMPLES:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(47); b = W(47 + 25)
sage: a.is_equal_to(b)
False
sage: a.is_equal_to(b, 7)
True
Returns whether the valuation of self is at least absprec. If absprec is None, returns if self is indistinguishable from zero.
If self is an inexact zero of valuation less than absprec, raises a PrecisionError.
EXAMPLES:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: O(w^189).is_zero()
True
sage: W(0).is_zero()
True
sage: a = W(675)
sage: a.is_zero()
False
sage: a.is_zero(7)
True
sage: a.is_zero(21)
False
Returns a pAdicZZpXCAElement congruent to self but with absolute precision at least absprec. If setting absprec that high would violate the precision cap, raises a precision error.
Note that the new digits will not necessarily be zero.
EXAMPLES:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(345, 17); a
4*w^5 + 3*w^7 + w^9 + 3*w^10 + 2*w^11 + 4*w^12 + w^13 + 2*w^14 + 2*w^15 + O(w^17)
sage: b = a.lift_to_precision(19); b # indirect doctest
4*w^5 + 3*w^7 + w^9 + 3*w^10 + 2*w^11 + 4*w^12 + w^13 + 2*w^14 + 2*w^15 + w^17 + 2*w^18 + O(w^19)
sage: c = a.lift_to_precision(24); c
4*w^5 + 3*w^7 + w^9 + 3*w^10 + 2*w^11 + 4*w^12 + w^13 + 2*w^14 + 2*w^15 + w^17 + 2*w^18 + 4*w^19 + 4*w^20 + 2*w^21 + 4*w^23 + O(w^24)
sage: a._ntl_rep()
[345]
sage: b._ntl_rep()
[345]
sage: c._ntl_rep()
[345]
Returns a list giving a series representation of self.
 times polynomials in the
generator (in the unramified case).
times polynomials in the
generator (in the unramified case).![[0,p-1]](../../../_images/math/b044ef9b265492c0b5be649bca0e579813e9b875.png)
![[(1-p)/2, p/2]](../../../_images/math/ad3105a4d784e104d3276dba490aef03e88beb9a.png) .
.EXAMPLES:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: y = W(775, 19); y
w^10 + 4*w^12 + 2*w^14 + w^15 + 2*w^16 + 4*w^17 + w^18 + O(w^19)
sage: (y>>9).list()
[0, 1, 0, 4, 0, 2, 1, 2, 4, 1]
sage: (y>>9).list('smallest')
[0, 1, 0, -1, 0, 2, 1, 2, 0, 1]
sage: w^10 - w^12 + 2*w^14 + w^15 + 2*w^16 + w^18 + O(w^19)
w^10 + 4*w^12 + 2*w^14 + w^15 + 2*w^16 + 4*w^17 + w^18 + O(w^19)
sage: g = x^3 + 3*x + 3
sage: A.<a> = R.ext(g)
sage: y = 75 + 45*a + 1200*a^2; y
4*a*5 + (3*a^2 + a + 3)*5^2 + 4*a^2*5^3 + a^2*5^4 + O(5^5)
sage: y.list()
[[], [0, 4], [3, 1, 3], [0, 0, 4], [0, 0, 1]]
sage: y.list('smallest')
[[], [0, -1], [-2, 2, -2], [1], [0, 0, 2]]
sage: 5*((-2*5 + 25) + (-1 + 2*5)*a + (-2*5 + 2*125)*a^2)
4*a*5 + (3*a^2 + a + 3)*5^2 + 4*a^2*5^3 + a^2*5^4 + O(5^5)
sage: W(0).list()
[0]
sage: A(0,4).list()
[[]]
Returns the matrix of right multiplication by the element on
the power basis 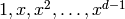 for this
extension field. Thus the rows of this matrix give the
images of each of the
for this
extension field. Thus the rows of this matrix give the
images of each of the 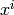 . The entries of the matrices are
IntegerMod elements, defined modulo p^(self.absprec() / e).
. The entries of the matrices are
IntegerMod elements, defined modulo p^(self.absprec() / e).
EXAMPLES:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = (3+w)^7
sage: a.matrix_mod_pn()
[2757 333 1068 725 2510]
[ 50 1507 483 318 725]
[ 500 50 3007 2358 318]
[1590 1375 1695 1032 2358]
[2415 590 2370 2970 1032]
Returns the absolute precision of self, ie the power of the uniformizer modulo which this element is defined.
EXAMPLES:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(75, 19); a
3*w^10 + 2*w^12 + w^14 + w^16 + w^17 + 3*w^18 + O(w^19)
sage: a.valuation()
10
sage: a.precision_absolute()
19
sage: a.precision_relative()
9
sage: a.unit_part()
3 + 2*w^2 + w^4 + w^6 + w^7 + 3*w^8 + O(w^9)
Returns the relative precision of self, ie the power of the uniformizer modulo which the unit part of self is defined.
EXAMPLES:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(75, 19); a
3*w^10 + 2*w^12 + w^14 + w^16 + w^17 + 3*w^18 + O(w^19)
sage: a.valuation()
10
sage: a.precision_absolute()
19
sage: a.precision_relative()
9
sage: a.unit_part()
3 + 2*w^2 + w^4 + w^6 + w^7 + 3*w^8 + O(w^9)
Returns self cast into the fraction field of self.parent().
EXAMPLES:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: z = (1 + w)^5; z
1 + w^5 + w^6 + 2*w^7 + 4*w^8 + 3*w^10 + w^12 + 4*w^13 + 4*w^14 + 4*w^15 + 4*w^16 + 4*w^17 + 4*w^20 + w^21 + 4*w^24 + O(w^25)
sage: y = z.to_fraction_field(); y #indirect doctest
1 + w^5 + w^6 + 2*w^7 + 4*w^8 + 3*w^10 + w^12 + 4*w^13 + 4*w^14 + 4*w^15 + 4*w^16 + 4*w^17 + 4*w^20 + w^21 + 4*w^24 + O(w^25)
sage: y.parent()
Eisenstein Extension of 5-adic Field with capped relative precision 5 in w defined by (1 + O(5^5))*x^5 + (O(5^6))*x^4 + (3*5^2 + O(5^6))*x^3 + (2*5 + 4*5^2 + 4*5^3 + 4*5^4 + 4*5^5 + O(5^6))*x^2 + (5^3 + O(5^6))*x + (4*5 + 4*5^2 + 4*5^3 + 4*5^4 + 4*5^5 + O(5^6))
Returns the unit part of self, ie self / uniformizer^(self.valuation())
EXAMPLES:
sage: R = ZpCA(5,5)
sage: S.<x> = ZZ[]
sage: f = x^5 + 75*x^3 - 15*x^2 +125*x - 5
sage: W.<w> = R.ext(f)
sage: a = W(75, 19); a
3*w^10 + 2*w^12 + w^14 + w^16 + w^17 + 3*w^18 + O(w^19)
sage: a.valuation()
10
sage: a.precision_absolute()
19
sage: a.precision_relative()
9
sage: a.unit_part()
3 + 2*w^2 + w^4 + w^6 + w^7 + 3*w^8 + O(w^9)