Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Probability »

This introduces a class of random variables, with the focus on discrete random variables (i.e. on a discrete probability space). This avoids the problem of defining a measure space and measurable functions.
Bases: sage.probability.random_variable.ProbabilitySpace_generic, sage.probability.random_variable.DiscreteRandomVariable
The discrete probability space
Bases: sage.probability.random_variable.RandomVariable_generic
A random variable on a discrete probability space.
The covariance of the discrete random variable X = self with Y = other.
Let  be the probability space of
be the probability space of  = self,
with probability function
= self,
with probability function  , and
, and 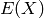 be the
expectation of
be the
expectation of  . Then the variance of
. Then the variance of  is:
is:
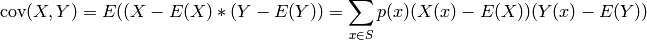
![\sum_{x \in S} p(x) X[x]](../../_images/math/7a4575a09d6c637373b0674f235dc3592256e2ea.png) , where
, where  = self and
= self and
 is the probability space of
is the probability space of  .
.The standard deviation of the discrete random variable.
Let  be the probability space of
be the probability space of  = self,
with probability function
= self,
with probability function  , and
, and 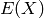 be the
expectation of
be the
expectation of  . Then the standard deviation of
. Then the standard deviation of
 is defined to be
is defined to be
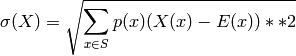
The covariance of the probability space X = self with image of Y = other under the given map of the probability space.
Let  be the probability space of
be the probability space of  = self,
with probability function
= self,
with probability function  , and
, and 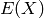 be the
expectation of
be the
expectation of  . Then the variance of
. Then the variance of  is:
is:
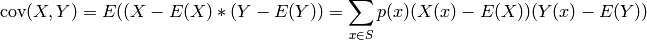
![\sum_{x \in S} p(x) X[e(x)]](../../_images/math/c7dabf28f7ffce4e779701568440d1fdce7a653c.png) , where
, where  = self,
= self,
 is the probability space of
is the probability space of  , and
, and
 = map.
= map.The standard deviation of the translated discrete random variable
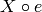 , where
, where  = self and
= self and  =
map.
=
map.
Let  be the probability space of
be the probability space of  = self,
with probability function
= self,
with probability function  , and
, and 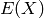 be the
expectation of
be the
expectation of  . Then the standard deviation of
. Then the standard deviation of
 is defined to be
is defined to be
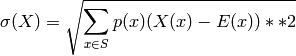
The variance of the discrete random variable 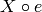 ,
where
,
where  = self, and
= self, and  = map.
= map.
Let  be the probability space of
be the probability space of  = self,
with probability function
= self,
with probability function  , and
, and 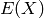 be the
expectation of
be the
expectation of  . Then the variance of
. Then the variance of  is:
is:
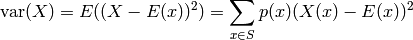
The variance of the discrete random variable.
Let  be the probability space of
be the probability space of  = self,
with probability function
= self,
with probability function  , and
, and 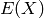 be the
expectation of
be the
expectation of  . Then the variance of
. Then the variance of  is:
is:
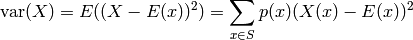
Bases: sage.probability.random_variable.RandomVariable_generic
A probability space.
Bases: sage.structure.parent_base.ParentWithBase
A random variable.