Probability Distributions

This module provides three types of probability distributions:

• RealDistribution: various real-valued probability distributions.
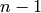• Spherica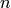lDistribution: uniformly distributed points on the surface of an sphere in dimensional euclidean space.
• GeneralDiscreteDistribution: user-defined discrete distributions.

AUTHORS:

• Josh Kantor (2007-02): first version
• William Stein (2007-02): rewrite of docs, conventions, etc.
• Carlo Hamalainen (2008-08): full doctest coverage, more documentation, GeneralDiscreteDistribution, misc fixes.

REFERENCES:

GNU gsl library, General discrete distributions http://www.gnu.org/software/gsl/manual/html_node/General-Discrete-Distributions.html

GNU gsl library, Random number distributions http://www.gnu.org/software/gsl/manual/html_node/Random-Number-Distributions.html

class sage.gsl.probability_distribution.GeneralDiscreteDistribution

Bases: sage.gsl.probability_distribution.ProbabilityDistribution

Create a discrete probability distribution.

INPUT:

• P - list of probabilities. The list will automatically be normalised if sum(P) is not equal to 1.
• rng - (optional) random number generator to use. May be one of 'default', 'luxury', or 'taus'.
• seed - (optional) seed to use with the random number generator.

OUTPUT:

• a probability distribution where the probability of selecting x is P[x].

EXAMPLES:

Constructs a GeneralDiscreteDistribution with the probability distribution 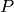where , , :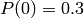

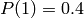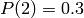sage: P = [0.3, 0.4, 0.3]
sage: X = GeneralDiscreteDistribution(P)
sage: X.get_random_element() # random
2

Checking the distribution of samples:

sage: P = [0.3, 0.4, 0.3]
sage: counts = [0] * len(P)
sage: X = GeneralDiscreteDistribution(P)
sage: nr_samples = 10000
sage: for _ in range(nr_samples):
...       counts[X.get_random_element()] += 1
sage: [1.0*x/nr_samples for x in counts] # random
[0.295400000000000, 0.400200000000000, 0.304400000000000]

The distribution probabilities will automatically be normalised:

sage: P = [0.1, 0.3]
sage: X = GeneralDiscreteDistribution(P, seed = 0)
sage: counts = [0, 0]
sage: for _ in range(10000):
...       counts[X.get_random_element()] += 1
sage: float(counts[1]/counts[0])
3.0420371867421179

get_random_element()

Get a random sample from the probability distribution.

EXAMPLE:

sage: P = [0.3, 0.4, 0.3]
sage: X = GeneralDiscreteDistribution(P)
sage: [X.get_random_element() for _ in range(10)] # random
[1, 0, 1, 1, 2, 0, 0, 2, 2, 0]

reset_distribution()

This method resets the distribution.

EXAMPLE:

sage: T = GeneralDiscreteDistribution([0.1, 0.3, 0.6])
sage: T.set_seed(0)
sage: [T.get_random_element() for _ in range(10)]
[2, 2, 2, 2, 2, 1, 2, 2, 1, 2]
sage: T.reset_distribution()
sage: [T.get_random_element() for _ in range(10)]
[2, 2, 2, 2, 2, 1, 2, 2, 1, 2]

set_random_number_generator(rng='default')

Set the random number generator to be used by gsl.

EXAMPLE:

sage: X = GeneralDiscreteDistribution([0.3, 0.4, 0.3])
sage: X.set_random_number_generator('taus')

set_seed(seed)

Set the seed to be used by the random number generator.

EXAMPLE:

sage: X = GeneralDiscreteDistribution([0.3, 0.4, 0.3])
sage: X.set_seed(1)
sage: X.get_random_element() # random
1

class sage.gsl.probability_distribution.ProbabilityDistribution

Bases: object

Concrete probability distributions should be derived from this abstract class.

generate_histogram_data(num_samples=1000, bins=50)

Compute a histogram of the probability distribution.

INPUT:

• num_samples - (optional) number of times to sample from the probability distribution
• bins - (optional) number of bins to divide the samples into.

OUTPUT:

• a tuple. The first element of the tuple is a list of length bins, consisting of the normalised histogram of the random samples. The second list is the bins.

EXAMPLE:

sage: from sage.gsl.probability_distribution import GeneralDiscreteDistribution
sage: P = [0.3, 0.4, 0.3]
sage: X = GeneralDiscreteDistribution(P)
sage: h, b = X.generate_histogram_data(bins = 10)
sage: h # random
[1.5249999999999995, 0.0, 0.0, 0.0, 0.0, 1.8649999999999995, 0.0, 0.0, 0.0, 1.6099999999999994]
sage: b # random
[0.0, 0.20000000000000001, 0.40000000000000002, 0.60000000000000009, 0.80000000000000004, 1.0, 1.2000000000000002, 1.4000000000000001, 1.6000000000000001, 1.8, 2.0]

generate_histogram_plot(name, num_samples=1000, bins=50)

Save the histogram from generate_histogram_data() to a file.

INPUT:

• name - file to save the histogram plot (as a PNG).
• num_samples - (optional) number of times to sample from the probability distribution
• bins - (optional) number of bins to divide the samples into.

EXAMPLE:

This saves the histogram plot to my_general_distribution_plot.png in the temporary directory SAGE_TMP:

sage: from sage.gsl.probability_distribution import GeneralDiscreteDistribution
sage: import os
sage: P = [0.3, 0.4, 0.3]
sage: X = GeneralDiscreteDistribution(P)
sage: file = os.path.join(SAGE_TMP, "my_general_distribution_plot")
sage: X.generate_histogram_plot(file)

get_random_element()

To be implemented by a derived class:

sage: P = sage.gsl.probability_distribution.ProbabilityDistribution()
sage: P.get_random_element()
...
NotImplementedError: implement in derived class

class sage.gsl.probability_distribution.RealDistribution

Bases: sage.gsl.probability_distribution.ProbabilityDistribution

The RealDistribution class provides a number of routines for sampling from and analyzing and visualizing probability distributions. For precise definitions of the distributions and their parameters see the gsl reference manuals chapter on random number generators and probability distributions.

EXAMPLES:

Uniform distribution on the interval [a, b]:

sage: a = 0
sage: b = 2
sage: T = RealDistribution('uniform', [a, b])
sage: T.get_random_element() # random
0.416921074037
sage: T.distribution_function(0)
0.5
sage: T.cum_distribution_function(1)
0.5
sage: T.cum_distribution_function_inv(.5)
1.0

The gaussian distribution takes 1 parameter sigma. The standard gaussian distribution has sigma = 1:

sage: sigma = 1
sage: T = RealDistribution('gaussian', sigma)
sage: T.get_random_element() # random
0.818610064197
sage: T.distribution_function(0)
0.398942280401
sage: T.cum_distribution_function(1)
0.841344746069
sage: T.cum_distribution_function_inv(.5)
0.0

The rayleigh distribution has 1 parameter sigma:

sage: sigma = 3
sage: T = RealDistribution('rayleigh', sigma)
sage: T.get_random_element() # random
1.65471291529
sage: T.distribution_function(0)
0.0
sage: T.cum_distribution_function(1)
0.0540405310932
sage: T.cum_distribution_function_inv(.5)
3.53223006755

The lognormal distribution has two parameters sigma and zeta:

sage: zeta = 0
sage: sigma = 1
sage: T = RealDistribution('lognormal', [zeta, sigma])
sage: T.get_random_element() # random
1.23541716538
sage: T.distribution_function(0)
0.0
sage: T.cum_distribution_function(1)
0.5
sage: T.cum_distribution_function_inv(.5)
1.0

The pareto distribution has two parameters a, and b:

sage: a = 1
sage: b = 1
sage: T = RealDistribution('pareto', [a, b])
sage: T.get_random_element() # random
1.16429443511
sage: T.distribution_function(0)
0.0
sage: T.cum_distribution_function(1)
0.0
sage: T.cum_distribution_function_inv(.5)
2.0

The student’s t distribution has one parameter nu:

sage: nu = 1
sage: T = RealDistribution('t', nu)
sage: T.get_random_element() # random
-0.994514581164
sage: T.distribution_function(0)
0.318309886184
sage: T.cum_distribution_function(1)
0.75
sage: T.cum_distribution_function_inv(.5)
0.0

The chi squared distribution has one parameter nu:

sage: nu = 1
sage: T = RealDistribution('chisquared', nu)
sage: T.get_random_element() # random
0.103230507883
sage: T.distribution_function(0)
0.0
sage: T.cum_distribution_function(1)
0.682689492137
sage: T.cum_distribution_function_inv(.5)
0.45493642312

The exponential power distribution has two parameters a and b:

sage: a = 1
sage: b = 2.5
sage: T = RealDistribution('exppow', [a, b])
sage: T.get_random_element() # random
0.570108609774
sage: T.distribution_function(0)
0.563530248993
sage: T.cum_distribution_function(1)
0.940263052543

The beta distribution has two parameters a and b:

sage: a = 2
sage: b = 2
sage: T = RealDistribution('beta', [a, b])
sage: T.get_random_element() # random
0.518139435862
sage: T.distribution_function(0)
0.0
sage: T.cum_distribution_function(1)
1.0

The weibull distribution has two parameters a and b:

sage: a = 1
sage: b = 1
sage: T = RealDistribution('weibull', [a, b])
sage: T.get_random_element() # random
1.86974582214
sage: T.distribution_function(0)
1.0
sage: T.cum_distribution_function(1)
0.632120558829
sage: T.cum_distribution_function_inv(.5)
0.69314718056

It is possible to select which random number generator drives the sampling as well as the seed. The default is the Mersenne twister. Also available are the RANDLXS algorithm and the Tausworthe generator (see the gsl reference manual for more details). These are all supposed to be simulation quality generators. For RANDLXS use rng = 'luxury' and for tausworth use rng = 'taus':

sage: T = RealDistribution('gaussian', 1, rng = 'luxury', seed = 10)

To change the seed at a later time use set_seed:

sage: T.set_seed(100)

cum_distribution_function(x)

Evaluate the cumulative distribution function of the probability distribution at x.

EXAMPLE:

sage: T = RealDistribution('uniform', [0, 2])
sage: T.cum_distribution_function(1)
0.5

cum_distribution_function_inv(x)

Evaluate the inverse of the cumulative distribution distribution function of the probability distribution at x.

EXAMPLE:

sage: T = RealDistribution('uniform', [0, 2])
sage: T.cum_distribution_function_inv(.5)
1.0

distribution_function(x)

Evaluate the distribution function of the probability distribution at x.

EXAMPLES:

sage: T = RealDistribution('uniform', [0, 2])
sage: T.distribution_function(0)
0.5
sage: T.distribution_function(1)
0.5
sage: T.distribution_function(1.5)
0.5
sage: T.distribution_function(2)
0.0

get_random_element()

Get a random sample the probability distribution.

EXAMPLE:

sage: T = RealDistribution('gaussian', 1, seed = 0)
sage: T.get_random_element()
0.133918608119

plot(*args, **kwds)

Plot the distribution function for the probability distribution. Parameters to sage.plot.plot.plot.plot can be passed through *args and **kwds.

EXAMPLE:

sage: T = RealDistribution('uniform', [0, 2])
sage: P = T.plot()

reset_distribution()

This method resets the distribution.

EXAMPLE:

sage: T = RealDistribution('gaussian', 1, seed = 10)
sage: [T.get_random_element() for _ in range(10)]
[0.133918608119, -0.0881009918314, 1.67440840625, 0.733641107293, 0.997524631602, -1.277502081, -2.39671528273, -0.679280164729, -0.0390913184336, 0.893555545521]
sage: T.reset_distribution()
sage: [T.get_random_element() for _ in range(10)]
[0.133918608119, -0.0881009918314, 1.67440840625, 0.733641107293, 0.997524631602, -1.277502081, -2.39671528273, -0.679280164729, -0.0390913184336, 0.893555545521]

set_distribution(name='uniform', parameters=[])

This method can be called to change the current probability distribution.

EXAMPLES:

sage: T = RealDistribution('gaussian', 1)
sage: T.set_distribution('gaussian', 1)
sage: T.set_distribution('pareto', [0, 1])

set_random_number_generator(rng='default')

Set the gsl random number generator to be one of default, luxury, or taus.

EXAMPLE:

sage: T = SphericalDistribution()
sage: T.set_random_number_generator('default')
sage: T.set_seed(0)
sage: T.get_random_element()
(0.0796156410464, -0.0523767162758, 0.995448657286)
sage: T.set_random_number_generator('luxury')
sage: T.set_seed(0)
sage: T.get_random_element()
(0.0796156410464, -0.0523767162758, 0.995448657286)

set_seed(seed)

Set the seed for the underlying random number generator.

EXAMPLE:

sage: T = RealDistribution('gaussian', 1, rng = 'luxury', seed = 10)
sage: T.set_seed(100)

class sage.gsl.probability_distribution.SphericalDistribution

Bases: sage.gsl.probability_distribution.ProbabilityDistribution

This class is capable of producing random points uniformly distributed on the surface of an n-1 sphere in n dimensional euclidean space. The dimension, n is selected via the keyword dimension. The random number generator which drives it can be selected using the keyword rng. Valid choices are default which uses the Mersenne-Twister, luxury which uses RANDLXS, and taus which uses the tausworth generator. The default dimension is 3.

EXAMPLES:

sage: T = SphericalDistribution()
sage: T.get_random_element() # random
(-0.872578667429, -0.29632873418, -0.388324285164)
sage: T = SphericalDistribution(dimension = 4, rng = 'luxury')
sage: T.get_random_element() # random
(-0.196597969334, -0.536955365418, -0.672242159448, -0.470232552109)

get_random_element()

Get a random sample from the probability distribution.

EXAMPLE:

sage: T = SphericalDistribution(seed = 0)
sage: T.get_random_element()
(0.0796156410464, -0.0523767162758, 0.995448657286)

reset_distribution()

This method resets the distribution.

EXAMPLE:

sage: T = SphericalDistribution(seed = 0)
sage: [T.get_random_element() for _ in range(4)]
[(0.0796156410464, -0.0523767162758, 0.995448657286), (0.412359949059, 0.560681785936, -0.718049585566), (-0.961986089162, -0.272647349404, -0.0156903512115), (0.567429757944, -0.0112067838004, -0.823345539732)]
sage: T.reset_distribution()
sage: [T.get_random_element() for _ in range(4)]
[(0.0796156410464, -0.0523767162758, 0.995448657286), (0.412359949059, 0.560681785936, -0.718049585566), (-0.961986089162, -0.272647349404, -0.0156903512115), (0.567429757944, -0.0112067838004, -0.823345539732)]

set_random_number_generator(rng='default')

Set the gsl random number generator to be one of default, luxury, or taus.

EXAMPLE:

sage: T = SphericalDistribution()
sage: T.set_random_number_generator('default')
sage: T.set_seed(0)
sage: T.get_random_element()
(0.0796156410464, -0.0523767162758, 0.995448657286)
sage: T.set_random_number_generator('luxury')
sage: T.set_seed(0)
sage: T.get_random_element()
(0.0796156410464, -0.0523767162758, 0.995448657286)

set_seed(seed)

Set the seed for the underlying random number generator.

EXAMPLE:

sage: T = SphericalDistribution(seed = 0)
sage: T.set_seed(100)