Free String Monoids¶

AUTHORS:

David Kohel <kohel@maths.usyd.edu.au>, 2007-01

Sage supports a wide range of specific free string monoids.

class sage.monoids.string_monoid.AlphabeticStringMonoid¶

Bases: sage.monoids.string_monoid.StringMonoid_class

The free alphabetic string monoid on generators A-Z.

EXAMPLES:

sage: S = AlphabeticStrings(); S
Free alphabetic string monoid on A-Z
sage: S.gen(0)
A
sage: S.gen(25)
Z
sage: S([ i for i in range(26) ])
ABCDEFGHIJKLMNOPQRSTUVWXYZ

characteristic_frequency(table_name='beker_piper')¶

Return a table of the characteristic frequency probability distribution of the English alphabet. In written English, various letters of the English alphabet occur more frequently than others. For example, the letter “E” appears more often than other vowels such as “A”, “I”, “O”, and “U”. In long works of written English such as books, the probability of a letter occurring tends to stabilize around a value. We call this value the characteristic frequency probability of the letter under consideration. When this probability is considered for each letter of the English alphabet, the resulting probabilities for all letters of this alphabet is referred to as the characteristic frequency probability distribution. Various studies report slightly different values for the characteristic frequency probability of an English letter. For instance, [Lew00] reports that “E” has a characteristic frequency probability of 0.12702, while [BekPip82] reports this value as 0.127. The concepts of characteristic frequency probability and characteristic frequency probability distribution can also be applied to non-empty alphabets other than the English alphabet.

The output of this method is different from that of the method frequency_distribution(). One can think of the characteristic frequency probability of an element in an alphabet $A$ as the expected probability of that element occurring. Let $S$ be a string encoded using elements of $A$ . The frequency probability distribution corresponding to $S$ provides us with the frequency probability of each element of $A$ as observed occurring in $S$ . Thus one distribution provides expected probabilities, while the other provides observed probabilities.

INPUT:

table_name – (default "beker_piper") the table of characteristic frequency probability distribution to use. The following tables are supported:
- "beker_piper" – the table of characteristic frequency probability distribution by Beker and Piper [BekPip82]. This is the default table to use.
- "lewand" – the table of characteristic frequency probability distribution by Lewand as described on page 36 of [Lew00].

OUTPUT:

A table of the characteristic frequency probability distribution of the English alphabet. This is a dictionary of letter/probability pairs.

EXAMPLES:

The characteristic frequency probability distribution table of Beker and Piper [BekPip82]:

sage: A = AlphabeticStrings()
sage: table = A.characteristic_frequency(table_name="beker_piper")
sage: sorted(table.items())
<BLANKLINE>
[('A', 0.0820000000000000),
('B', 0.0150000000000000),
('C', 0.0280000000000000),
('D', 0.0430000000000000),
('E', 0.127000000000000),
('F', 0.0220000000000000),
('G', 0.0200000000000000),
('H', 0.0610000000000000),
('I', 0.0700000000000000),
('J', 0.00200000000000000),
('K', 0.00800000000000000),
('L', 0.0400000000000000),
('M', 0.0240000000000000),
('N', 0.0670000000000000),
('O', 0.0750000000000000),
('P', 0.0190000000000000),
('Q', 0.00100000000000000),
('R', 0.0600000000000000),
('S', 0.0630000000000000),
('T', 0.0910000000000000),
('U', 0.0280000000000000),
('V', 0.0100000000000000),
('W', 0.0230000000000000),
('X', 0.00100000000000000),
('Y', 0.0200000000000000),
('Z', 0.00100000000000000)]

The characteristic frequency probability distribution table of Lewand [Lew00]:

sage: table = A.characteristic_frequency(table_name="lewand")
sage: sorted(table.items())
<BLANKLINE>
[('A', 0.0816700000000000),
('B', 0.0149200000000000),
('C', 0.0278200000000000),
('D', 0.0425300000000000),
('E', 0.127020000000000),
('F', 0.0222800000000000),
('G', 0.0201500000000000),
('H', 0.0609400000000000),
('I', 0.0696600000000000),
('J', 0.00153000000000000),
('K', 0.00772000000000000),
('L', 0.0402500000000000),
('M', 0.0240600000000000),
('N', 0.0674900000000000),
('O', 0.0750700000000000),
('P', 0.0192900000000000),
('Q', 0.000950000000000000),
('R', 0.0598700000000000),
('S', 0.0632700000000000),
('T', 0.0905600000000000),
('U', 0.0275800000000000),
('V', 0.00978000000000000),
('W', 0.0236000000000000),
('X', 0.00150000000000000),
('Y', 0.0197400000000000),
('Z', 0.000740000000000000)]

Illustrating the difference between characteristic_frequency() and frequency_distribution():

sage: A = AlphabeticStrings()
sage: M = A.encoding("abcd")
sage: FD = M.frequency_distribution().function()
sage: sorted(FD.items())
<BLANKLINE>
[(A, 0.250000000000000),
(B, 0.250000000000000),
(C, 0.250000000000000),
(D, 0.250000000000000)]
sage: CF = A.characteristic_frequency()
sage: sorted(CF.items())
<BLANKLINE>
[('A', 0.0820000000000000),
('B', 0.0150000000000000),
('C', 0.0280000000000000),
('D', 0.0430000000000000),
('E', 0.127000000000000),
('F', 0.0220000000000000),
('G', 0.0200000000000000),
('H', 0.0610000000000000),
('I', 0.0700000000000000),
('J', 0.00200000000000000),
('K', 0.00800000000000000),
('L', 0.0400000000000000),
('M', 0.0240000000000000),
('N', 0.0670000000000000),
('O', 0.0750000000000000),
('P', 0.0190000000000000),
('Q', 0.00100000000000000),
('R', 0.0600000000000000),
('S', 0.0630000000000000),
('T', 0.0910000000000000),
('U', 0.0280000000000000),
('V', 0.0100000000000000),
('W', 0.0230000000000000),
('X', 0.00100000000000000),
('Y', 0.0200000000000000),
('Z', 0.00100000000000000)]

TESTS:

The table name must be either “beker_piper” or “lewand”:

sage: table = A.characteristic_frequency(table_name="")
...
ValueError: Table name must be either 'beker_piper' or 'lewand'.
sage: table = A.characteristic_frequency(table_name="none")
...
ValueError: Table name must be either 'beker_piper' or 'lewand'.

REFERENCES:

[BekPip82]

(1, 2, 3) H. Beker and F. Piper. Cipher Systems: The Protection of Communications. John Wiley and Sons, 1982.

[Lew00]

(1, 2, 3) Robert Edward Lewand. Cryptological Mathematics. The Mathematical Association of America, 2000.

encoding(S)¶

The encoding of the string S in the alphabetic string monoid, obtained by the monoid homomorphism

A -> A, ..., Z -> Z, a -> A, ..., z -> Z

and stripping away all other characters. It should be noted that this is a non-injective monoid homomorphism.

EXAMPLES:

sage: S = AlphabeticStrings()
sage: s = S.encoding("The cat in the hat."); s
THECATINTHEHAT
sage: s.decoding()
'THECATINTHEHAT'

sage.monoids.string_monoid.AlphabeticStrings()¶

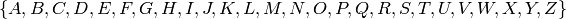Returns the string monoid on generators A-Z: $\{ A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z \}$ .

OUTPUT:

Free alphabetic string monoid on A-Z.

EXAMPLES:

sage: S = AlphabeticStrings(); S
Free alphabetic string monoid on A-Z
sage: x = S.gens()
sage: x[0]
A
sage: x[25]
Z

class sage.monoids.string_monoid.BinaryStringMonoid¶

Bases: sage.monoids.string_monoid.StringMonoid_class

The free binary string monoid on generators 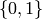$\{ 0, 1 \}$ .

encoding(S, padic=False)¶

The binary encoding of the string S, as a binary string element.

The default is to keep the standard ASCII byte encoding, e.g.

A = 65 -> 01000001
B = 66 -> 01000010
.
.
.
Z = 90 -> 01001110

rather than a 2-adic representation 65 -> 10000010.

Set padic=True to reverse the bit string.

EXAMPLES:

sage: S = BinaryStrings()
sage: S.encoding('A')
01000001
sage: S.encoding('A',padic=True)
10000010
sage: S.encoding(' ',padic=True)
00000100

sage.monoids.string_monoid.BinaryStrings()¶

Returns the free binary string monoid on generators 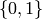$\{ 0, 1 \}$ .

OUTPUT:

Free binary string monoid.

EXAMPLES:

sage: S = BinaryStrings(); S
Free binary string monoid
sage: u = S('')
sage: u

sage: x = S('0')
sage: x
0
sage: y = S('1')
sage: y
1
sage: z = S('01110')
sage: z
01110
sage: x*y^3*x == z
True
sage: u*x == x*u
True

class sage.monoids.string_monoid.HexadecimalStringMonoid¶

Bases: sage.monoids.string_monoid.StringMonoid_class

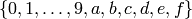The free hexadecimal string monoid on generators $\{ 0, 1, \dots, 9, a, b, c, d, e, f \}$ .

encoding(S, padic=False)¶

The encoding of the string S as a hexadecimal string element.

The default is to keep the standard right-to-left byte encoding, e.g.

A = '\x41' -> 41
B = '\x42' -> 42
.
.
.
Z = '\x5a' -> 5a

rather than a left-to-right representation A = 65 -> 14. Although standard (e.g., in the Python constructor ‘xhh’), this can be confusing when the string reads left-to-right.

Set padic=True to reverse the character encoding.

EXAMPLES:

sage: S = HexadecimalStrings()
sage: S.encoding('A')
41
sage: S.encoding('A',padic=True)
14
sage: S.encoding(' ',padic=False)
20
sage: S.encoding(' ',padic=True)
02

sage.monoids.string_monoid.HexadecimalStrings()¶

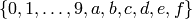Returns the free hexadecimal string monoid on generators $\{ 0, 1, \dots , 9, a, b, c, d, e, f \}$ .

OUTPUT:

Free hexadecimal string monoid.

EXAMPLES:

sage: S = HexadecimalStrings(); S
Free hexadecimal string monoid
sage: x = S.gen(0)
sage: y = S.gen(10)
sage: z = S.gen(15)
sage: z
f
sage: x*y^3*z
0aaaf

class sage.monoids.string_monoid.OctalStringMonoid¶

Bases: sage.monoids.string_monoid.StringMonoid_class

The free octal string monoid on generators 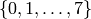$\{ 0, 1, \dots, 7 \}$ .

sage.monoids.string_monoid.OctalStrings()¶

Returns the free octal string monoid on generators 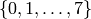$\{ 0, 1, \dots, 7 \}$ .

OUTPUT:

Free octal string monoid.

EXAMPLES:

sage: S = OctalStrings(); S
Free octal string monoid
sage: x = S.gens()
sage: x[0]
0
sage: x[7]
7
sage: x[0] * x[3]^3 * x[5]^4 * x[6]
033355556

class sage.monoids.string_monoid.Radix64StringMonoid¶

Bases: sage.monoids.string_monoid.StringMonoid_class

The free radix 64 string monoid on 64 generators.

sage.monoids.string_monoid.Radix64Strings()¶

Returns the free radix 64 string monoid on 64 generators

A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z,
a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z,
0,1,2,3,4,5,6,7,8,9,+,/

OUTPUT:

Free radix 64 string monoid.

EXAMPLES:

sage: S = Radix64Strings(); S
Free radix 64 string monoid
sage: x = S.gens()
sage: x[0]
A
sage: x[62]
+
sage: x[63]
/

class sage.monoids.string_monoid.StringMonoid_class(n, alphabet=())¶

Bases: sage.monoids.free_monoid.FreeMonoid_class

A free string monoid on $n$ generators.

alphabet()¶

gen(i=0)¶

The $i$ -th generator of the monoid.

INPUT:

i – integer (default: 0)

EXAMPLES:

sage: S = BinaryStrings()
sage: S.gen(0)
0
sage: S.gen(1)
1
sage: S.gen(2)
...
IndexError: Argument i (= 2) must be between 0 and 1.
sage: S = HexadecimalStrings()
sage: S.gen(0)
0
sage: S.gen(12)
c
sage: S.gen(16)
...
IndexError: Argument i (= 16) must be between 0 and 15.

Free String Monoids¶

Previous topic

Next topic

This Page

Navigation

Free String Monoids¶

Previous topic

Next topic

This Page

Quick search

Navigation