AUTHORS:
TODO: Change to use a get_unsafe / set_unsafe, etc., structure exactly like with matrices, since we’ll have to define a bunch of special purpose implementations of vectors easily and systematically.
EXAMPLES: We create a vector space over  and a
subspace of this space.
and a
subspace of this space.
sage: V = QQ^5
sage: W = V.span([V.1, V.2])
Arithmetic operations always return something in the ambient space,
since there is a canonical map from 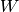 to
to 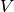 but
not from
but
not from 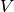 to
to 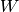 .
.
sage: parent(W.0 + V.1)
Vector space of dimension 5 over Rational Field
sage: parent(V.1 + W.0)
Vector space of dimension 5 over Rational Field
sage: W.0 + V.1
(0, 2, 0, 0, 0)
sage: W.0 - V.0
(-1, 1, 0, 0, 0)
Next we define modules over  and a finite
field.
and a finite
field.
sage: K = ZZ^5
sage: M = GF(7)^5
Arithmetic between the  and
and
 modules is defined, and the result is always
over
modules is defined, and the result is always
over  , since there is a canonical coercion map
to
, since there is a canonical coercion map
to  .
.
sage: K.0 + V.1
(1, 1, 0, 0, 0)
sage: parent(K.0 + V.1)
Vector space of dimension 5 over Rational Field
Since there is no canonical coercion map to the finite field from
 the following arithmetic is not defined:
the following arithmetic is not defined:
sage: V.0 + M.0
...
TypeError: unsupported operand parent(s) for '+': 'Vector space of dimension 5 over Rational Field' and 'Vector space of dimension 5 over Finite Field of size 7'
However, there is a map from  to the finite
field, so the following is defined, and the result is in the finite
field.
to the finite
field, so the following is defined, and the result is in the finite
field.
sage: w = K.0 + M.0; w
(2, 0, 0, 0, 0)
sage: parent(w)
Vector space of dimension 5 over Finite Field of size 7
sage: parent(M.0 + K.0)
Vector space of dimension 5 over Finite Field of size 7
Matrix vector multiply:
sage: MS = MatrixSpace(QQ,3)
sage: A = MS([0,1,0,1,0,0,0,0,1])
sage: V = QQ^3
sage: v = V([1,2,3])
sage: v * A
(2, 1, 3)
TESTS:
sage: D = 46341
sage: u = 7
sage: R = Integers(D)
sage: p = matrix(R,[[84, 97, 55, 58, 51]])
sage: 2*p.row(0)
(168, 194, 110, 116, 102)
Bases: sage.structure.element.Vector
An element of a generic free module.
EXAMPLES:
sage: V = vector(ZZ, [5, 9, 13, 15])
sage: V.Mod(7)
(5, 2, 6, 1)
sage: parent(V.Mod(7))
Vector space of dimension 4 over Ring of integers modulo 7
Return the additive order of self.
EXAMPLES:
sage: v = vector(Integers(4), [1,2])
sage: v.additive_order()
4
sage: v = vector([1,2,3])
sage: v.additive_order()
+Infinity
sage: v = vector(Integers(30), [6, 15]); v
(6, 15)
sage: v.additive_order()
10
sage: 10*v
(0, 0)
Apply the given map phi (an arbitrary Python function or callable object) to this free module element. If R is not given, automatically determine the base ring of the resulting element.
OUTPUT: a free module element over R
EXAMPLES:
sage: m = vector([1,x,sin(x+1)])
sage: m.apply_map(lambda x: x^2)
(1, x^2, sin(x + 1)^2)
sage: m.apply_map(sin)
(sin(1), sin(x), sin(sin(x + 1)))
sage: m = vector(ZZ, 9, range(9))
sage: k.<a> = GF(9)
sage: m.apply_map(k)
(0, 1, 2, 0, 1, 2, 0, 1, 2)
In this example, we explicitly specify the codomain.
sage: s = GF(3)
sage: f = lambda x: s(x)
sage: n = m.apply_map(f, k); n
(0, 1, 2, 0, 1, 2, 0, 1, 2)
sage: n.parent()
Vector space of dimension 9 over Finite Field in a of size 3^2
If your map sends 0 to a non-zero value, then your resulting vector is not mathematically sparse:
sage: v = vector([0] * 6 + [1], sparse=True); v
(0, 0, 0, 0, 0, 0, 1)
sage: v2 = v.apply_map(lambda x: x+1); v2
(1, 1, 1, 1, 1, 1, 2)
but it’s still represented with a sparse data type:
sage: parent(v2)
Ambient sparse free module of rank 7 over the principal ideal domain Integer Ring
This data type is inefficient for dense vectors, so you may want to specify sparse=False:
sage: v2 = v.apply_map(lambda x: x+1, sparse=False); v2
(1, 1, 1, 1, 1, 1, 2)
sage: parent(v2)
Ambient free module of rank 7 over the principal ideal domain Integer Ring
Or if you have a map that will result in mostly zeroes, you may want to specify sparse=True:
sage: v = vector(srange(10))
sage: v2 = v.apply_map(lambda x: 0 if x else 1, sparse=True); v2
(1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
sage: parent(v2)
Ambient sparse free module of rank 10 over the principal ideal domain Integer Ring
TESTS:
sage: m = vector(SR,[])
sage: m.apply_map(lambda x: x*x) == m
True
Check that we don’t unnecessarily apply phi to 0 in the sparse case:
sage: m = vector(ZZ, range(1, 4), sparse=True)
sage: m.apply_map(lambda x: 1/x)
(1, 1/2, 1/3)
sage: parent(vector(RDF, (), sparse=True).apply_map(lambda x: x, sparse=True))
Sparse vector space of dimension 0 over Real Double Field
sage: parent(vector(RDF, (), sparse=True).apply_map(lambda x: x, sparse=False))
Vector space of dimension 0 over Real Double Field
sage: parent(vector(RDF, (), sparse=False).apply_map(lambda x: x, sparse=True))
Sparse vector space of dimension 0 over Real Double Field
sage: parent(vector(RDF, (), sparse=False).apply_map(lambda x: x, sparse=False))
Vector space of dimension 0 over Real Double Field
Change the base ring of this vector, by coercing each element of this vector into R.
EXAMPLES:
sage: v = vector(QQ['x,y'], [1..5]); v.change_ring(GF(3))
(1, 2, 0, 1, 2)
Return the cross product of self and right, which is only defined for vectors of length 3 or 7.
INPUT:
OUTPUT:
The cross product (vector product) of self and right, a vector of the same size of self and right.
This product is performed under the assumption that the basis vectors are orthonormal.
EXAMPLES:
sage: v = vector([1,2,3]); w = vector([0,5,-9])
sage: v.cross_product(v)
(0, 0, 0)
sage: u = v.cross_product(w); u
(-33, 9, 5)
sage: u.dot_product(v)
0
sage: u.dot_product(w)
0
The cross product is defined for degree seven vectors as well. [WIKIPEDIA:CROSSPRODUCT] The 3-D cross product is achieved using the quaternians, whereas the 7-D cross product is achieved using the octions.
sage: u = vector(QQ, [1, -1/3, 57, -9, 56/4, -4,1])
sage: v = vector(QQ, [37, 55, -99/57, 9, -12, 11/3, 4/98])
sage: u.cross_product(v)
(1394815/2793, -2808401/2793, 39492/49, -48737/399, -9151880/2793, 62513/2793, -326603/171)
The degree seven cross product is anticommutative.
sage: u.cross_product(v) + v.cross_product(u)
(0, 0, 0, 0, 0, 0, 0)
The degree seven cross product is distributive across addition.
sage: v = vector([-12, -8/9, 42, 89, -37, 60/99, 73])
sage: u = vector([31, -42/7, 97, 80, 30/55, -32, 64])
sage: w = vector([-25/4, 40, -89, -91, -72/7, 79, 58])
sage: v.cross_product(u + w) - (v.cross_product(u) + v.cross_product(w))
(0, 0, 0, 0, 0, 0, 0)
The degree seven cross product respects scalar multiplication.
sage: v = vector([2, 17, -11/5, 21, -6, 2/17, 16])
sage: u = vector([-8, 9, -21, -6, -5/3, 12, 99])
sage: (5*v).cross_product(u) - 5*(v.cross_product(u))
(0, 0, 0, 0, 0, 0, 0)
sage: v.cross_product(5*u) - 5*(v.cross_product(u))
(0, 0, 0, 0, 0, 0, 0)
sage: (5*v).cross_product(u) - (v.cross_product(5*u))
(0, 0, 0, 0, 0, 0, 0)
The degree seven cross product respects the scalar triple product.
sage: v = vector([2,6,-7/4,-9/12,-7,12,9])
sage: u = vector([22,-7,-9/11,12,15,15/7,11])
sage: w = vector([-11,17,19,-12/5,44,21/56,-8])
sage: v.dot_product(u.cross_product(w)) - w.dot_product(v.cross_product(u))
0
TESTS:
Both vectors need to be of length three or both vectors need to be of length seven.
sage: u = vector(range(7))
sage: v = vector(range(3))
sage: u.cross_product(v)
...
ArithmeticError: Cross product only defined for vectors of length three or seven, not (7 and 3)
REFERENCES:
| [WIKIPEDIA:CROSSPRODUCT] | Algebraic Properties of the Cross Product http://en.wikipedia.org/wiki/Cross_product |
AUTHOR:
Billy Wonderly (2010-05-11), Added 7-D Cross Product
Return the degree of this vector, which is simply the number of entries.
EXAMPLES:
sage: sage.modules.free_module_element.FreeModuleElement(QQ^389).degree()
389
sage: vector([1,2/3,8]).degree()
3
Return the least common multiple of the denominators of the entries of self.
EXAMPLES:
sage: v = vector([1/2,2/5,3/14])
sage: v.denominator()
70
sage: 2*5*7
70
Return dense version of self. If self is dense, just return self; otherwise, create and return correspond dense vector.
EXAMPLES:
sage: vector([-1,0,3,0,0,0]).dense_vector().is_dense()
True
sage: vector([-1,0,3,0,0,0],sparse=True).dense_vector().is_dense()
True
sage: vector([-1,0,3,0,0,0],sparse=True).dense_vector()
(-1, 0, 3, 0, 0, 0)
Derivative with respect to variables supplied in args.
Multiple variables and iteration counts may be supplied; see documentation for the global derivative() function for more details.
diff() is an alias of this function.
EXAMPLES:
sage: v = vector([1,x,x^2])
sage: v.derivative(x)
(0, 1, 2*x)
sage: type(v.derivative(x)) == type(v)
True
sage: v = vector([1,x,x^2], sparse=True)
sage: v.derivative(x)
(0, 1, 2*x)
sage: type(v.derivative(x)) == type(v)
True
sage: v.derivative(x,x)
(0, 0, 2)
Return dictionary of nonzero entries of self.
INPUT:
- copy – bool (default: True)
OUTPUT:
- Python dictionary
EXAMPLES:
sage: v = vector([0,0,0,0,1/2,0,3/14])
sage: v.dict()
{4: 1/2, 6: 3/14}
In some cases when copy=False, we get back a dangerous reference:
sage: v = vector({0:5, 2:3/7}, sparse=True)
sage: v.dict(copy=False)
{0: 5, 2: 3/7}
sage: v.dict(copy=False)[0] = 18
sage: v
(18, 0, 3/7)
Derivative with respect to variables supplied in args.
Multiple variables and iteration counts may be supplied; see documentation for the global derivative() function for more details.
diff() is an alias of this function.
EXAMPLES:
sage: v = vector([1,x,x^2])
sage: v.derivative(x)
(0, 1, 2*x)
sage: type(v.derivative(x)) == type(v)
True
sage: v = vector([1,x,x^2], sparse=True)
sage: v.derivative(x)
(0, 1, 2*x)
sage: type(v.derivative(x)) == type(v)
True
sage: v.derivative(x,x)
(0, 0, 2)
Return the dot product of self and right, which is the sum of the product of the corresponding entries.
INPUT:
EXAMPLES:
sage: V = FreeModule(ZZ, 3)
sage: v = V([1,2,3])
sage: w = V([4,5,6])
sage: v.dot_product(w)
32
sage: W = VectorSpace(GF(3),3)
sage: w = W([0,1,2])
sage: w.dot_product(v)
2
sage: w.dot_product(v).parent()
Finite Field of size 3
Implicit coercion is well defined (regardless of order), so we get 2 even if we do the dot product in the other order.
sage: v.dot_product(w)
2
Simply returns self. This is useful, since for many objects, self.element() returns a vector corresponding to self.
EXAMPLES:
sage: v = vector([1/2,2/5,0]); v
(1/2, 2/5, 0)
sage: v.element()
(1/2, 2/5, 0)
The get method is in some cases more efficient (and more dangerous) than __getitem__, because it is not guaranteed to do any error checking.
EXAMPLES:
sage: vector([1/2,2/5,0]).get(0)
1/2
sage: vector([1/2,2/5,0]).get(3)
...
IndexError: index out of range
Returns the inner product of self and other, with respect to the inner product defined on the parent of self.
EXAMPLES:
sage: I = matrix(ZZ,3,[2,0,-1,0,2,0,-1,0,6])
sage: M = FreeModule(ZZ, 3, inner_product_matrix = I)
sage: (M.0).inner_product(M.0)
2
sage: K = M.span_of_basis([[0/2,-1/2,-1/2], [0,1/2,-1/2],[2,0,0]])
sage: (K.0).inner_product(K.0)
2
Returns a symbolic integral of the vector, component-wise.
integrate() is an alias of the function.
EXAMPLES:
sage: t=var('t')
sage: r=vector([t,t^2,sin(t)])
sage: r.integral(t)
(1/2*t^2, 1/3*t^3, -cos(t))
sage: integrate(r,t)
(1/2*t^2, 1/3*t^3, -cos(t))
sage: r.integrate(t,0,1)
(1/2, 1/3, -cos(1) + 1)
Returns a symbolic integral of the vector, component-wise.
integrate() is an alias of the function.
EXAMPLES:
sage: t=var('t')
sage: r=vector([t,t^2,sin(t)])
sage: r.integral(t)
(1/2*t^2, 1/3*t^3, -cos(t))
sage: integrate(r,t)
(1/2*t^2, 1/3*t^3, -cos(t))
sage: r.integrate(t,0,1)
(1/2, 1/3, -cos(1) + 1)
Return True if this is a dense vector, which is just a statement about the data structure, not the number of nonzero entries.
EXAMPLES:
sage: vector([1/2,2/5,0]).is_dense()
True
sage: vector([1/2,2/5,0],sparse=True).is_dense()
False
Return True if this vector is immutable, i.e., the entries cannot be changed.
EXAMPLES:
sage: v = vector(QQ['x,y'], [1..5]); v.is_immutable()
False
sage: v.set_immutable()
sage: v.is_immutable()
True
Return True if this vector is mutable, i.e., the entries can be changed.
EXAMPLES:
sage: v = vector(QQ['x,y'], [1..5]); v.is_mutable()
True
sage: v.set_immutable()
sage: v.is_mutable()
False
Return True if this is a sparse vector, which is just a statement about the data structure, not the number of nonzero entries.
EXAMPLES:
sage: vector([1/2,2/5,0]).is_sparse()
False
sage: vector([1/2,2/5,0],sparse=True).is_sparse()
True
Return True, since this is a vector.
EXAMPLES:
sage: vector([1/2,2/5,0]).is_vector()
True
Return iterator over self.
EXAMPLES:
sage: v = vector([1,2/3,pi])
sage: v.iteritems()
<dictionary-itemiterator object at ...>
sage: list(v.iteritems())
[(0, 1), (1, 2/3), (2, pi)]
EXAMPLES:
sage: V = vector(Integers(7), [5, 9, 13, 15]) ; V
(5, 2, 6, 1)
sage: V.lift()
(5, 2, 6, 1)
sage: parent(V.lift())
Ambient free module of rank 4 over the principal ideal domain Integer Ring
Return list of elements of self.
INPUT:
- copy – bool, whether returned list is a copy that is safe to change
EXAMPLES:
sage: v = vector([1,2/3,8], sparse=True)
sage: v.list()
[1, 2/3, 8]
Return list of elements chosen from this vector using the given positions of this vector.
INPUT:
- positions – iterable of ints
EXAMPLES:
sage: v = vector([1,2/3,pi])
sage: v.list_from_positions([0,0,0,2,1])
[1, 1, 1, pi, 2/3]
Returns a numeric integral of the vector, component-wise, and the result of the nintegral command on each component of the input.
nintegrate() is an alias of the function.
EXAMPLES:
sage: t=var('t')
sage: r=vector([t,t^2,sin(t)])
sage: vec,answers=r.nintegral(t,0,1)
sage: vec
(0.5, 0.333333333333, 0.459697694132)
sage: type(vec)
<type 'sage.modules.vector_real_double_dense.Vector_real_double_dense'>
sage: answers
[(0.5, 5.5511151231257843e-15, 21, 0),
(0.33333333333333343, 3.7007434154171903e-15, 21, 0),
(0.45969769413186018, 5.1036696439228408e-15, 21, 0)]
sage: r=vector([t,0,1], sparse=True)
sage: r.nintegral(t,0,1)
((0.5, 0.0, 1.0),
{0: (0.5, 5.5511151231257843e-15, 21, 0),
2: (1.0, 1.110223024625157e-14, 21, 0)})
Returns a numeric integral of the vector, component-wise, and the result of the nintegral command on each component of the input.
nintegrate() is an alias of the function.
EXAMPLES:
sage: t=var('t')
sage: r=vector([t,t^2,sin(t)])
sage: vec,answers=r.nintegral(t,0,1)
sage: vec
(0.5, 0.333333333333, 0.459697694132)
sage: type(vec)
<type 'sage.modules.vector_real_double_dense.Vector_real_double_dense'>
sage: answers
[(0.5, 5.5511151231257843e-15, 21, 0),
(0.33333333333333343, 3.7007434154171903e-15, 21, 0),
(0.45969769413186018, 5.1036696439228408e-15, 21, 0)]
sage: r=vector([t,0,1], sparse=True)
sage: r.nintegral(t,0,1)
((0.5, 0.0, 1.0),
{0: (0.5, 5.5511151231257843e-15, 21, 0),
2: (1.0, 1.110223024625157e-14, 21, 0)})
Return the sorted list of integers i such that self[i] != 0.
EXAMPLES:
sage: vector([-1,0,3,0,0,0,0.01]).nonzero_positions()
[0, 2, 6]
Return the p-norm of this vector, where p can be a real number
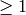 , Infinity, or a symbolic expression. If
, Infinity, or a symbolic expression. If 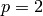 (default),
this is the usual Euclidean norm; if p=Infinity, this is the
maximum norm; if
(default),
this is the usual Euclidean norm; if p=Infinity, this is the
maximum norm; if 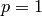 , this is the taxicab (Manhattan) norm.
, this is the taxicab (Manhattan) norm.
EXAMPLES:
sage: v = vector([1,2,-3])
sage: v.norm(5)
276^(1/5)
The default is the usual Euclidean norm:
sage: v.norm()
sqrt(14)
sage: v.norm(2)
sqrt(14)
The infinity norm is the maximum size of any entry:
sage: v.norm(Infinity)
3
Any real or symbolic value works:
sage: v=vector(RDF,[1,2,3])
sage: v.norm(5)
3.07738488539
sage: v.norm(pi/2)
4.2165958647
sage: _=var('a b c d p'); v=vector([a, b, c, d])
sage: v.norm(p)
(abs(a)^p + abs(b)^p + abs(c)^p + abs(d)^p)^(1/p)
Return this vector divided through by the first nonzero entry of this vector.
EXAMPLES:
sage: v = vector(QQ,[0,4/3,5,1,2])
sage: v.normalize()
(0, 1, 15/4, 3/4, 3/2)
Return the pairwise product of self and right, which is a vector of the products of the corresponding entries.
INPUT:
EXAMPLES:
sage: V = FreeModule(ZZ, 3)
sage: v = V([1,2,3])
sage: w = V([4,5,6])
sage: v.pairwise_product(w)
(4, 10, 18)
sage: sum(v.pairwise_product(w)) == v.dot_product(w)
True
sage: W = VectorSpace(GF(3),3)
sage: w = W([0,1,2])
sage: w.pairwise_product(v)
(0, 2, 0)
sage: w.pairwise_product(v).parent()
Vector space of dimension 3 over Finite Field of size 3
Implicit coercion is well defined (regardless of order), so we get 2 even if we do the dot product in the other order.
sage: v.pairwise_product(w).parent()
Vector space of dimension 3 over Finite Field of size 3
TESTS:
sage: x, y = var('x, y')
sage: parent(vector(ZZ,[1,2]).pairwise_product(vector(ZZ,[1,2])))
Ambient free module of rank 2 over the principal ideal domain Integer Ring
sage: parent(vector(ZZ,[1,2]).pairwise_product(vector(QQ,[1,2])))
Vector space of dimension 2 over Rational Field
sage: parent(vector(QQ,[1,2]).pairwise_product(vector(ZZ,[1,2])))
Vector space of dimension 2 over Rational Field
sage: parent(vector(QQ,[1,2]).pairwise_product(vector(QQ,[1,2])))
Vector space of dimension 2 over Rational Field
sage: parent(vector(QQ,[1,2,3,4]).pairwise_product(vector(ZZ[x],[1,2,3,4])))
Ambient free module of rank 4 over the principal ideal domain Univariate Polynomial Ring in x over Rational Field
sage: parent(vector(ZZ[x],[1,2,3,4]).pairwise_product(vector(QQ,[1,2,3,4])))
Ambient free module of rank 4 over the principal ideal domain Univariate Polynomial Ring in x over Rational Field
sage: parent(vector(QQ,[1,2,3,4]).pairwise_product(vector(ZZ[x][y],[1,2,3,4])))
Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in y over Univariate Polynomial Ring in x over Rational Field
sage: parent(vector(ZZ[x][y],[1,2,3,4]).pairwise_product(vector(QQ,[1,2,3,4])))
Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in y over Univariate Polynomial Ring in x over Rational Field
sage: parent(vector(QQ[x],[1,2,3,4]).pairwise_product(vector(ZZ[x][y],[1,2,3,4])))
Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in y over Univariate Polynomial Ring in x over Rational Field
sage: parent(vector(ZZ[x][y],[1,2,3,4]).pairwise_product(vector(QQ[x],[1,2,3,4])))
Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in y over Univariate Polynomial Ring in x over Rational Field
sage: parent(vector(QQ[y],[1,2,3,4]).pairwise_product(vector(ZZ[x][y],[1,2,3,4])))
Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in y over Univariate Polynomial Ring in x over Rational Field
sage: parent(vector(ZZ[x][y],[1,2,3,4]).pairwise_product(vector(QQ[y],[1,2,3,4])))
Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in y over Univariate Polynomial Ring in x over Rational Field
sage: parent(vector(ZZ[x],[1,2,3,4]).pairwise_product(vector(ZZ[y],[1,2,3,4])))
...
TypeError: no common canonical parent for objects with parents: 'Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in x over Integer Ring' and 'Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in y over Integer Ring'
sage: parent(vector(ZZ[x],[1,2,3,4]).pairwise_product(vector(QQ[y],[1,2,3,4])))
...
TypeError: no common canonical parent for objects with parents: 'Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in x over Integer Ring' and 'Ambient free module of rank 4 over the principal ideal domain Univariate Polynomial Ring in y over Rational Field'
sage: parent(vector(QQ[x],[1,2,3,4]).pairwise_product(vector(ZZ[y],[1,2,3,4])))
...
TypeError: no common canonical parent for objects with parents: 'Ambient free module of rank 4 over the principal ideal domain Univariate Polynomial Ring in x over Rational Field' and 'Ambient free module of rank 4 over the integral domain Univariate Polynomial Ring in y over Integer Ring'
sage: parent(vector(QQ[x],[1,2,3,4]).pairwise_product(vector(QQ[y],[1,2,3,4])))
...
TypeError: no common canonical parent for objects with parents: 'Ambient free module of rank 4 over the principal ideal domain Univariate Polynomial Ring in x over Rational Field' and 'Ambient free module of rank 4 over the principal ideal domain Univariate Polynomial Ring in y over Rational Field'
sage: v = vector({1: 1, 3: 2}) # test sparse vectors
sage: w = vector({0: 6, 3: -4})
sage: v.pairwise_product(w)
(0, 0, 0, -8)
sage: w.pairwise_product(v) == v.pairwise_product(w)
True
INPUT:
otherwise ‘step’) type of plot. Options are:
Both ‘arrow’ and ‘point’ raise exceptions if the vector has more than 3 dimensions.
EXAMPLES:
sage: v = vector(RDF, (1,2))
sage: eps = 0.1
sage: plot(v, plot_type='arrow')
sage: plot(v, plot_type='point')
sage: plot(v, plot_type='step') # calls v.plot_step()
sage: plot(v, plot_type='step', eps=eps, xmax=5, hue=0)
sage: v = vector(RDF, (1,2,1))
sage: plot(v) # defaults to an arrow plot
sage: plot(v, plot_type='arrow')
sage: from sage.plot.plot3d.shapes2 import frame3d
sage: plot(v, plot_type='point')+frame3d((0,0,0), v.list())
sage: plot(v, plot_type='step') # calls v.plot_step()
sage: plot(v, plot_type='step', eps=eps, xmax=5, hue=0)
sage: v = vector(RDF, (1,2,3,4))
sage: plot(v) # defaults to a step plot
INPUT:
EXAMPLES:
sage: eps=0.1
sage: v = vector(RDF, [sin(n*eps) for n in range(100)])
sage: v.plot_step(eps=eps, xmax=5, hue=0)
The set method is meant to be more efficient than __setitem__, because it need not be guaranteed to do any error checking or coercion. Use with great, great care.
EXAMPLES:
sage: v = vector([1/2,2/5,0]); v
(1/2, 2/5, 0)
sage: v.set(2, -15/17); v
(1/2, 2/5, -15/17)
Make this vector immutable. This operation can’t be undone.
EXAMPLES:
sage: v = vector([1..5]); v
(1, 2, 3, 4, 5)
sage: v[1] = 10
sage: v.set_immutable()
sage: v[1] = 10
...
ValueError: vector is immutable; please change a copy instead (use copy())
Return sparse version of self. If self is sparse, just return self; otherwise, create and return correspond sparse vector.
EXAMPLES:
sage: vector([-1,0,3,0,0,0]).sparse_vector().is_sparse()
True
sage: vector([-1,0,3,0,0,0]).sparse_vector().is_sparse()
True
sage: vector([-1,0,3,0,0,0]).sparse_vector()
(-1, 0, 3, 0, 0, 0)
EXAMPLES:
sage: var('a,b,d,e')
(a, b, d, e)
sage: v = vector([a, b, d, e])
sage: v.substitute(a=1)
(1, b, d, e)
sage: v.subs(a=b, b=d)
(b, d, d, e)
Return the integers i such that self[i] != 0. This is the same as the nonzero_positions function.
EXAMPLES:
sage: vector([-1,0,3,0,0,0,0.01]).support()
[0, 2, 6]
Return self as a column matrix.
EXAMPLES:
sage: v = vector(ZZ, [2, 12, 22])
sage: transpose(vector(v))
[ 2]
[12]
[22]
sage: transpose(vector(GF(7), v))
[2]
[5]
[1]
sage: transpose(vector(v, ZZ['x', 'y']))
[ 2]
[12]
[22]
Bases: sage.modules.free_module_element.FreeModuleElement
A generic dense element of a free module.
Returns a vector over a callable symbolic expression ring.
EXAMPLES:
sage: x,y=var('x,y')
sage: v=vector([x,y,x*sin(y)])
sage: w=v.function([x,y]); w
((x, y) |--> x, (x, y) |--> y, (x, y) |--> x*sin(y))
sage: w.base_ring()
Callable function ring with arguments (x, y)
sage: w(1,2)
(1, 2, sin(2))
sage: w(2,1)
(2, 1, 2*sin(1))
sage: w(y=1,x=2)
(2, 1, 2*sin(1))
sage: x,y=var('x,y')
sage: v=vector([x,y,x*sin(y)])
sage: w=v.function([x]); w
(x |--> x, x |--> y, x |--> x*sin(y))
sage: w.base_ring()
Callable function ring with arguments (x,)
sage: w(4)
(4, y, 4*sin(y))
Return list of elements of self.
INPUT:
- copy – bool, return list of underlying entries
EXAMPLES:
sage: v = vector([1,2/3,pi])
sage: type(v)
<type 'sage.modules.free_module_element.FreeModuleElement_generic_dense'>
sage: a = v.list(); a
[1, 2/3, pi]
sage: a[0] = 20; v
(1, 2/3, pi)
sage: a = v.list(copy=False); a
[1, 2/3, pi]
sage: a[0] = 20; v
(20, 2/3, pi)
sage: v
(20, 2/3, pi)
Returns a numerical approximation of self by calling the n() method on all of its entries.
EXAMPLES:
sage: v = vector(RealField(212), [1,2,3])
sage: v.n()
(1.00000000000000, 2.00000000000000, 3.00000000000000)
sage: _.parent()
Vector space of dimension 3 over Real Field with 53 bits of precision
sage: v.n(prec=75)
(1.000000000000000000000, 2.000000000000000000000, 3.000000000000000000000)
sage: _.parent()
Vector space of dimension 3 over Real Field with 75 bits of precision
Bases: sage.modules.free_module_element.FreeModuleElement
A generic sparse free module element is a dictionary with keys ints i and entries in the base ring.
EXAMPLES:
Pickling works:
sage: v = FreeModule(ZZ, 3, sparse=True).0
sage: loads(dumps(v)) == v
True
sage: v = FreeModule(Integers(8)['x,y'], 5, sparse=True).1
sage: loads(dumps(v)) - v
(0, 0, 0, 0, 0)
sage: a = vector([-1,0,1/1],sparse=True); b = vector([-1/1,0,0],sparse=True)
sage: a.parent()
Sparse vector space of dimension 3 over Rational Field
sage: b - a
(0, 0, -1)
sage: (b-a).dict()
{2: -1}
Return the least common multiple of the denominators of the entries of self.
EXAMPLES:
sage: v = vector([1/2,2/5,3/14], sparse=True)
sage: v.denominator()
70
Return dictionary of nonzero entries of self.
INPUT:
- copy – bool (default: True)
OUTPUT:
- Python dictionary
EXAMPLES:
sage: v = vector([0,0,0,0,1/2,0,3/14], sparse=True)
sage: v.dict()
{4: 1/2, 6: 3/14}
Like __getitem__ but with no guaranteed type or bounds checking. Returns 0 if access is out of bounds.
EXAMPLES:
sage: v = vector([1,2/3,pi], sparse=True)
sage: v.get(1)
2/3
sage: v.get(10)
0
Return iterator over the entries of self.
EXAMPLES:
sage: v = vector([1,2/3,pi], sparse=True)
sage: v.iteritems()
<dictionary-itemiterator object at ...>
sage: list(v.iteritems())
[(0, 1), (1, 2/3), (2, pi)]
Return list of elements of self.
INPUT:
- copy – bool, return list of underlying entries
EXAMPLES:
sage: v = vector([1,2/3,pi], sparse=True)
sage: type(v)
<type 'sage.modules.free_module_element.FreeModuleElement_generic_sparse'>
sage: a = v.list(); a
[1, 2/3, pi]
Returns a numerical approximation of self by calling the n() method on all of its entries.
EXAMPLES:
sage: v = vector(RealField(200), [1,2,3], sparse=True)
sage: v.n()
(1.00000000000000, 2.00000000000000, 3.00000000000000)
sage: _.parent()
Sparse vector space of dimension 3 over Real Field with 53 bits of precision
sage: v.n(prec=75)
(1.000000000000000000000, 2.000000000000000000000, 3.000000000000000000000)
sage: _.parent()
Sparse vector space of dimension 3 over Real Field with 75 bits of precision
Returns the list of numbers i such that self[i] != 0.
EXAMPLES:
sage: v = vector({1: 1, 3: -2})
sage: w = vector({1: 4, 3: 2})
sage: v+w
(0, 5, 0, 0)
sage: (v+w).nonzero_positions()
[1]
Like __setitem__ but with no guaranteed type or bounds checking.
EXAMPLES:
sage: v = vector([1,2/3,pi], sparse=True)
sage: v.set(1, pi^3)
sage: v
(1, pi^3, pi)
No bounds checking:
sage: v.set(10, pi)
This lack of bounds checking causes trouble later:
sage: v
...
IndexError: list assignment index out of range
Return a vector over R with given entries.
CALL FORMATS:
In each case, give sparse=True or sparse=False as an option.
INPUT:
OUTPUT: An element of the free module over R of rank len(elts).
EXAMPLES:
sage: v = vector([1,2,3]); v
(1, 2, 3)
sage: v.parent()
Ambient free module of rank 3 over the principal ideal domain Integer Ring
sage: v = vector([1,2,3/5]); v
(1, 2, 3/5)
sage: v.parent()
Vector space of dimension 3 over Rational Field
All entries must canonically coerce to some common ring:
sage: v = vector([17, GF(11)(5), 19/3]); v
...
TypeError: unable to find a common ring for all elements
sage: v = vector([17, GF(11)(5), 19]); v
(6, 5, 8)
sage: v.parent()
Vector space of dimension 3 over Finite Field of size 11
sage: v = vector([17, GF(11)(5), 19], QQ); v
(17, 5, 19)
sage: v.parent()
Vector space of dimension 3 over Rational Field
sage: v = vector((1,2,3), QQ); v
(1, 2, 3)
sage: v.parent()
Vector space of dimension 3 over Rational Field
sage: v = vector(QQ, (1,2,3)); v
(1, 2, 3)
sage: v.parent()
Vector space of dimension 3 over Rational Field
sage: v = vector(vector([1,2,3])); v
(1, 2, 3)
sage: v.parent()
Ambient free module of rank 3 over the principal ideal domain Integer Ring
You can also use free_module_element, which is the same as vector.
sage: free_module_element([1/3, -4/5])
(1/3, -4/5)
Make a vector mod 3 out of a vector over  :
:
sage: vector(vector([1,2,3]), GF(3))
(1, 2, 0)
Here we illustrate the creation of sparse vectors by using a dictionary:
sage: vector({1:1.1, 3:3.14})
(0.000000000000000, 1.10000000000000, 0.000000000000000, 3.14000000000000)
Any 1 dimensional numpy array of type float or complex may be passed to vector. The result will be a vector in the appropriate dimensional vector space over the real double field or the complex double field. The data in the array must be contiguous so column-wise slices of numpy matrices will raise an exception.
sage: import numpy
sage: x=numpy.random.randn(10)
sage: y=vector(x)
sage: v=numpy.random.randn(10)*numpy.complex(0,1)
sage: w=vector(v)
If any of the arguments to vector have Python type int, long, real, or complex, they will first be coerced to the appropriate Sage objects. This fixes trac #3847:
sage: v = vector([int(0)]); v
(0)
sage: v[0].parent()
Integer Ring
sage: v = vector(range(10)); v
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
sage: v[3].parent()
Integer Ring
sage: v = vector([float(23.4), int(2), complex(2+7*I), long(1)]); v
(23.4, 2.0, 2.0 + 7.0*I, 1.0)
sage: v[1].parent()
Complex Double Field
If the argument is a vector, it doesn’t change the base ring. This fixes trac #6643:
sage: K.<sqrt3> = QuadraticField(3)
sage: u = vector(K, (1/2, sqrt3/2) )
sage: vector(u).base_ring()
Number Field in sqrt3 with defining polynomial x^2 - 3
sage: v = vector(K, (0, 1) )
sage: vector(v).base_ring()
Number Field in sqrt3 with defining polynomial x^2 - 3
EXAMPLES:
sage: sage.modules.free_module_element.is_FreeModuleElement(0)
False
sage: sage.modules.free_module_element.is_FreeModuleElement(vector([1,2,3]))
True
EXAMPLES:
sage: sage.modules.free_module_element.make_FreeModuleElement_generic_dense(QQ^3, [1,2,-3/7], 3)
(1, 2, -3/7)
EXAMPLES:
sage: v = sage.modules.free_module_element.make_FreeModuleElement_generic_dense_v1(QQ^3, [1,2,-3/7], 3, True); v
(1, 2, -3/7)
sage: v[0] = 10; v
(10, 2, -3/7)
sage: v = sage.modules.free_module_element.make_FreeModuleElement_generic_dense_v1(QQ^3, [1,2,-3/7], 3, False); v
(1, 2, -3/7)
sage: v[0] = 10
...
ValueError: vector is immutable; please change a copy instead (use copy())
EXAMPLES:
sage: v = sage.modules.free_module_element.make_FreeModuleElement_generic_sparse(QQ^3, {2:5/2}, 3); v
(0, 0, 5/2)
EXAMPLES:
sage: v = sage.modules.free_module_element.make_FreeModuleElement_generic_sparse_v1(QQ^3, {2:5/2}, 3, False); v
(0, 0, 5/2)
sage: v.is_mutable()
False
Find a common ring (using R as universe) that contains every element of v, and replace v with the sequence of elements in v coerced to this ring. For more details, see the sage.structure.sequence.Sequence object.
INPUT:
- v – list or tuple
- R – ring or None
EXAMPLES:
sage: sage.modules.free_module_element.prepare([1,2/3,5],None)
([1, 2/3, 5], Rational Field)
sage: sage.modules.free_module_element.prepare([1,2/3,5],RR)
([1.00000000000000, 0.666666666666667, 5.00000000000000], Real Field with 53 bits of precision)
sage: sage.modules.free_module_element.prepare([1,2/3,'10',5],None)
...
TypeError: unable to find a common ring for all elements
sage: sage.modules.free_module_element.prepare([1,2/3,'10',5],RR)
([1.00000000000000, 0.666666666666667, 10.0000000000000, 5.00000000000000], Real Field with 53 bits of precision)
EXAMPLES:
sage: from sage.modules.free_module_element import prepare_dict
sage: prepare_dict({3:1 , 5:3}, QQ)
([0, 0, 0, 1, 0, 3], Rational Field)
sage: prepare_dict({},QQ)
([], Rational Field)
Return a vector over R with given entries.
CALL FORMATS:
In each case, give sparse=True or sparse=False as an option.
INPUT:
OUTPUT: An element of the free module over R of rank len(elts).
EXAMPLES:
sage: v = vector([1,2,3]); v
(1, 2, 3)
sage: v.parent()
Ambient free module of rank 3 over the principal ideal domain Integer Ring
sage: v = vector([1,2,3/5]); v
(1, 2, 3/5)
sage: v.parent()
Vector space of dimension 3 over Rational Field
All entries must canonically coerce to some common ring:
sage: v = vector([17, GF(11)(5), 19/3]); v
...
TypeError: unable to find a common ring for all elements
sage: v = vector([17, GF(11)(5), 19]); v
(6, 5, 8)
sage: v.parent()
Vector space of dimension 3 over Finite Field of size 11
sage: v = vector([17, GF(11)(5), 19], QQ); v
(17, 5, 19)
sage: v.parent()
Vector space of dimension 3 over Rational Field
sage: v = vector((1,2,3), QQ); v
(1, 2, 3)
sage: v.parent()
Vector space of dimension 3 over Rational Field
sage: v = vector(QQ, (1,2,3)); v
(1, 2, 3)
sage: v.parent()
Vector space of dimension 3 over Rational Field
sage: v = vector(vector([1,2,3])); v
(1, 2, 3)
sage: v.parent()
Ambient free module of rank 3 over the principal ideal domain Integer Ring
You can also use free_module_element, which is the same as vector.
sage: free_module_element([1/3, -4/5])
(1/3, -4/5)
Make a vector mod 3 out of a vector over  :
:
sage: vector(vector([1,2,3]), GF(3))
(1, 2, 0)
Here we illustrate the creation of sparse vectors by using a dictionary:
sage: vector({1:1.1, 3:3.14})
(0.000000000000000, 1.10000000000000, 0.000000000000000, 3.14000000000000)
Any 1 dimensional numpy array of type float or complex may be passed to vector. The result will be a vector in the appropriate dimensional vector space over the real double field or the complex double field. The data in the array must be contiguous so column-wise slices of numpy matrices will raise an exception.
sage: import numpy
sage: x=numpy.random.randn(10)
sage: y=vector(x)
sage: v=numpy.random.randn(10)*numpy.complex(0,1)
sage: w=vector(v)
If any of the arguments to vector have Python type int, long, real, or complex, they will first be coerced to the appropriate Sage objects. This fixes trac #3847:
sage: v = vector([int(0)]); v
(0)
sage: v[0].parent()
Integer Ring
sage: v = vector(range(10)); v
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
sage: v[3].parent()
Integer Ring
sage: v = vector([float(23.4), int(2), complex(2+7*I), long(1)]); v
(23.4, 2.0, 2.0 + 7.0*I, 1.0)
sage: v[1].parent()
Complex Double Field
If the argument is a vector, it doesn’t change the base ring. This fixes trac #6643:
sage: K.<sqrt3> = QuadraticField(3)
sage: u = vector(K, (1/2, sqrt3/2) )
sage: vector(u).base_ring()
Number Field in sqrt3 with defining polynomial x^2 - 3
sage: v = vector(K, (0, 1) )
sage: vector(v).base_ring()
Number Field in sqrt3 with defining polynomial x^2 - 3