 -adic weights¶
-adic weights¶A  -adic weight is a continuous character
-adic weight is a continuous character 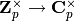 . These are the
. These are the  -points of a rigid space over
-points of a rigid space over
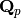 , which is isomorphic to a disjoint union of copies (indexed by
, which is isomorphic to a disjoint union of copies (indexed by
 ) of the open unit
) of the open unit  -adic disc.
-adic disc.
Sage supports both “classical points”, which are determined by the data of a
Dirichlet character modulo 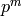 for some
for some 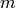 and an integer
and an integer  (corresponding
to the character
(corresponding
to the character 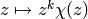 ) and “non-classical points” which are
determined by the data of an element of
) and “non-classical points” which are
determined by the data of an element of  and
an element
and
an element 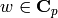 with
with 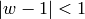 .
.
EXAMPLES:
sage: W = pAdicWeightSpace(17)
sage: W
Space of 17-adic weight-characters defined over '17-adic Field with capped relative precision 20'
sage: L = Qp(17).extension(x^2 - 17, names='a'); L.rename('L')
sage: W.base_extend(L)
Space of 17-adic weight-characters defined over 'L'
We create a simple element of  : the algebraic character,
: the algebraic character, 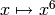 :
:
sage: kappa = W(6)
sage: kappa(5)
15625
sage: kappa(5) == 5^6
True
A locally algebraic character, 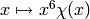 for
for 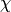 a Dirichlet
character mod
a Dirichlet
character mod  :
:
sage: kappa2 = W(6, DirichletGroup(17, Qp(17)).0^8)
sage: kappa2(5) == -5^6
True
sage: kappa2(13) == 13^6
True
A non-locally-algebraic character, sending the generator 18 of 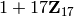 to 35 and acting as
to 35 and acting as 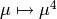 on the group of 16th
roots of unity:
on the group of 16th
roots of unity:
sage: kappa3 = W(35 + O(17^20), 4, algebraic=False)
sage: kappa3(2)
16 + 8*17 + ... + O(17^20)
AUTHORS:
Bases: sage.modular.overconvergent.weightspace.WeightCharacter
A point in weight space corresponding to a locally algebraic character, of
the form 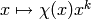 where
where  is an integer and
is an integer and 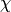 is a
Dirichlet character modulo
is a
Dirichlet character modulo  for some
for some  .
.
TESTS:
sage: w = pAdicWeightSpace(23)(12, DirichletGroup(23, QQ).0) # exact
sage: w == loads(dumps(w))
True
sage: w = pAdicWeightSpace(23)(12, DirichletGroup(23, Qp(23)).0) # inexact
sage: w == loads(dumps(w))
True
sage: w is loads(dumps(w)) # elements are not globally unique
False
Return the value of the p-adic L-function of  evaluated at
this weight-character. If the character is
evaluated at
this weight-character. If the character is 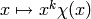 where
where 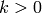 and
and 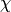 has conductor a power of
has conductor a power of  , this is an
element of the number field generated by the values of
, this is an
element of the number field generated by the values of 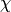 , equal to
the value of the complex L-function
, equal to
the value of the complex L-function 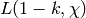 . If
. If 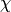 is
trivial, it is equal to
is
trivial, it is equal to  .
.
At present this is not implemented in any other cases, except the
trivial character (for which the value is 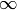 ).
).
TODO: Implement this more generally using the Amice transform machinery in sage/schemes/elliptic_curves/padic_lseries.py, which should clearly be factored out into a separate class.
EXAMPLES:
sage: pAdicWeightSpace(7)(4).Lvalue() == (1 - 7^3)*zeta__exact(-3)
True
sage: pAdicWeightSpace(7)(5, DirichletGroup(7, Qp(7)).0^4).Lvalue()
0
sage: pAdicWeightSpace(7)(6, DirichletGroup(7, Qp(7)).0^4).Lvalue()
1 + 2*7 + 7^2 + 3*7^3 + 3*7^5 + 4*7^6 + 2*7^7 + 5*7^8 + 2*7^9 + 3*7^10 + 6*7^11 + 2*7^12 + 3*7^13 + 5*7^14 + 6*7^15 + 5*7^16 + 3*7^17 + 6*7^18 + O(7^19)
If this character is 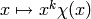 for an integer
for an integer  and a
Dirichlet character
and a
Dirichlet character 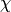 , return
, return 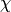 .
.
EXAMPLE:
sage: kappa = pAdicWeightSpace(29)(13, DirichletGroup(29, Qp(29)).0^14)
sage: kappa.chi()
Dirichlet character modulo 29 of conductor 29 mapping 2 |--> 28 + 28*29 + 28*29^2 + ... + O(29^20)
If this character is 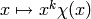 for an integer
for an integer  and a
Dirichlet character
and a
Dirichlet character 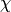 , return
, return  .
.
EXAMPLE:
sage: kappa = pAdicWeightSpace(29)(13, DirichletGroup(29, Qp(29)).0^14)
sage: kappa.k()
13
Return the Teichmuller type of this weight-character  , which is
the unique
, which is
the unique 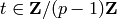 such that
such that 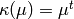 for mu a
for mu a 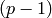 -st root of 1.
-st root of 1.
For 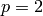 this doesn’t make sense, but we still want the Teichmuller
type to correspond to the index of the component of weight space in
which
this doesn’t make sense, but we still want the Teichmuller
type to correspond to the index of the component of weight space in
which  lies, so we return 1 if
lies, so we return 1 if  is odd and 0 otherwise.
is odd and 0 otherwise.
EXAMPLE:
sage: pAdicWeightSpace(11)(2, DirichletGroup(11,QQ).0).teichmuller_type()
7
sage: pAdicWeightSpace(29)(13, DirichletGroup(29, Qp(29)).0).teichmuller_type()
14
sage: pAdicWeightSpace(2)(3, DirichletGroup(4,QQ).0).teichmuller_type()
0
Bases: sage.modular.overconvergent.weightspace.WeightCharacter
Return the Teichmuller type of this weight-character  , which is
the unique
, which is
the unique 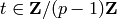 such that
such that 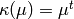 for mu a
for mu a 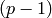 -st root of 1.
-st root of 1.
For 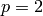 this doesn’t make sense, but we still want the Teichmuller
type to correspond to the index of the component of weight space in
which
this doesn’t make sense, but we still want the Teichmuller
type to correspond to the index of the component of weight space in
which  lies, so we return 1 if
lies, so we return 1 if  is odd and 0 otherwise.
is odd and 0 otherwise.
EXAMPLES:
sage: pAdicWeightSpace(17)(1 + 3*17 + 2*17^2 + O(17^3), 8, False).teichmuller_type()
8
sage: pAdicWeightSpace(2)(1 + 2 + O(2^2), 1, False).teichmuller_type()
1
Bases: sage.structure.element.Element
Abstract base class representing an element of the p-adic weight space
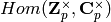 .
.
Return the value of the p-adic L-function of  , which can be
regarded as a rigid-analytic function on weight space, evaluated at
this character.
, which can be
regarded as a rigid-analytic function on weight space, evaluated at
this character.
EXAMPLES:
sage: W = pAdicWeightSpace(11)
sage: sage.modular.overconvergent.weightspace.WeightCharacter(W).Lvalue()
...
NotImplementedError
Extend scalars to the base ring R (which must have a canonical map from the current base ring)
EXAMPLE:
sage: w = pAdicWeightSpace(17, QQ)(3)
sage: w.base_extend(Qp(17))
3
Return True if this weight-character sends -1 to +1.
EXAMPLE:
sage: pAdicWeightSpace(17)(0).is_even()
True
sage: pAdicWeightSpace(17)(11).is_even()
False
sage: pAdicWeightSpace(17)(1 + 17 + O(17^20), 3, False).is_even()
False
sage: pAdicWeightSpace(17)(1 + 17 + O(17^20), 4, False).is_even()
True
Return True if and only if this is the trivial character.
EXAMPLES:
sage: pAdicWeightSpace(11)(2).is_trivial()
False
sage: pAdicWeightSpace(11)(2, DirichletGroup(11, QQ).0).is_trivial()
False
sage: pAdicWeightSpace(11)(0).is_trivial()
True
Return the reciprocal of the p-adic L-function evaluated at this weight-character. If the weight-character is odd, then the L-function is zero, so an error will be raised.
EXAMPLES:
sage: pAdicWeightSpace(11)(4).one_over_Lvalue()
-12/133
sage: pAdicWeightSpace(11)(3, DirichletGroup(11, QQ).0).one_over_Lvalue()
-1/6
sage: pAdicWeightSpace(11)(3).one_over_Lvalue()
...
ZeroDivisionError: Rational division by zero
sage: pAdicWeightSpace(11)(0).one_over_Lvalue()
0
sage: type(_)
<type 'sage.rings.integer.Integer'>
Calculate the q-expansion of the p-adic Eisenstein series of given weight-character, normalised so the constant term is 1.
EXAMPLE:
sage: kappa = pAdicWeightSpace(3)(3, DirichletGroup(3,QQ).0)
sage: kappa.pAdicEisensteinSeries(QQ[['q']], 20)
1 - 9*q + 27*q^2 - 9*q^3 - 117*q^4 + 216*q^5 + 27*q^6 - 450*q^7 + 459*q^8 - 9*q^9 - 648*q^10 + 1080*q^11 - 117*q^12 - 1530*q^13 + 1350*q^14 + 216*q^15 - 1845*q^16 + 2592*q^17 + 27*q^18 - 3258*q^19 + O(q^20)
If  is this character, calculate the values
is this character, calculate the values 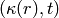 where
where  is
is  (or 5 if
(or 5 if 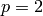 ) and
) and 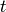 is the unique element of
is the unique element of
 such that
such that 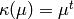 for
for 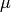 a (p-1)st root of unity. (If
a (p-1)st root of unity. (If 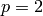 , we take
, we take 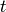 to be 0 or 1
according to whether
to be 0 or 1
according to whether  is odd or even.) These two values
uniquely determine the character
is odd or even.) These two values
uniquely determine the character  .
.
EXAMPLES:
sage: W=pAdicWeightSpace(11); W(2).values_on_gens()
(1 + 2*11 + 11^2 + O(11^20), 2)
sage: W(2, DirichletGroup(11, QQ).0).values_on_gens()
(1 + 2*11 + 11^2 + O(11^20), 7)
sage: W(1 + 2*11 + O(11^5), 4, algebraic = False).values_on_gens()
(1 + 2*11 + O(11^5), 4)
Bases: sage.structure.parent_base.ParentWithBase
The space of  -adic weight-characters
-adic weight-characters 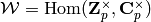 . This isomorphic to a
disjoint union of
. This isomorphic to a
disjoint union of 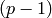 open discs of radius 1 (or 2 such discs if
open discs of radius 1 (or 2 such discs if 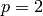 ), with the parameter on the open disc corresponding to the image of
), with the parameter on the open disc corresponding to the image of  (or 5 if
(or 5 if 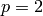 )
)
TESTS:
sage: W = pAdicWeightSpace(3)
sage: W is loads(dumps(W))
True
Extend scalars to the ring R. There must be a canonical coercion map from the present base ring to R.
EXAMPLE:
sage: W = pAdicWeightSpace(3, QQ)
sage: W.base_extend(Qp(3))
Space of 3-adic weight-characters defined over '3-adic Field with capped relative precision 20'
sage: W.base_extend(IntegerModRing(12))
...
TypeError: No coercion map from 'Rational Field' to 'Ring of integers modulo 12' is defined
Return the prime  such that this is a
such that this is a  -adic weight space.
-adic weight space.
EXAMPLE:
sage: pAdicWeightSpace(17).prime()
17
Construct the p-adic weight space for the given prime p. A  -adic weight
is a continuous character
-adic weight
is a continuous character  .
These are the
.
These are the  -points of a rigid space over
-points of a rigid space over 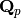 ,
which is isomorphic to a disjoint union of copies (indexed by
,
which is isomorphic to a disjoint union of copies (indexed by
 ) of the open unit
) of the open unit  -adic disc.
-adic disc.
Note that the “base ring” of a  -adic weight is the smallest ring
containing the image of
-adic weight is the smallest ring
containing the image of  ; in particular, although the default base
ring is
; in particular, although the default base
ring is 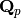 , base ring
, base ring  will also work.
will also work.
EXAMPLES:
sage: pAdicWeightSpace(3) # indirect doctest
Space of 3-adic weight-characters defined over '3-adic Field with capped relative precision 20'
sage: pAdicWeightSpace(3, QQ)
Space of 3-adic weight-characters defined over 'Rational Field'
sage: pAdicWeightSpace(10)
...
ValueError: p must be prime