Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Modular Symbols »

Bases: sage.modular.modsym.space.ModularSymbolsSpace, sage.modular.hecke.submodule.HeckeSubmodule
Subspace of ambient space of modular symbols
The boundary map to the corresponding space of boundary modular symbols. (This is the restriction of the map on the ambient space.)
EXAMPLES:
sage: M = ModularSymbols(1, 24, sign=1) ; M
Modular Symbols space of dimension 3 for Gamma_0(1) of weight 24 with sign 1 over Rational Field
sage: M.basis()
([X^18*Y^4,(0,0)], [X^20*Y^2,(0,0)], [X^22,(0,0)])
sage: M.cuspidal_submodule().basis()
([X^18*Y^4,(0,0)], [X^20*Y^2,(0,0)])
sage: M.eisenstein_submodule().basis()
([X^18*Y^4,(0,0)] + 166747/324330*[X^20*Y^2,(0,0)] + 236364091/6742820700*[X^22,(0,0)],)
sage: M.boundary_map()
Hecke module morphism boundary map defined by the matrix
[ 0]
[ 0]
[-1]
Domain: Modular Symbols space of dimension 3 for Gamma_0(1) of weight ...
Codomain: Space of Boundary Modular Symbols for Modular Group SL(2,Z) ...
sage: M.cuspidal_subspace().boundary_map()
Hecke module morphism defined by the matrix
[0]
[0]
Domain: Modular Symbols subspace of dimension 2 of Modular Symbols space ...
Codomain: Space of Boundary Modular Symbols for Modular Group SL(2,Z) ...
sage: M.eisenstein_submodule().boundary_map()
Hecke module morphism defined by the matrix
[-236364091/6742820700]
Domain: Modular Symbols subspace of dimension 1 of Modular Symbols space ...
Codomain: Space of Boundary Modular Symbols for Modular Group SL(2,Z) ...
Return the cuspidal subspace of this subspace of modular symbols.
EXAMPLES:
sage: S = ModularSymbols(42,4).cuspidal_submodule() ; S
Modular Symbols subspace of dimension 40 of Modular Symbols space of dimension 48 for Gamma_0(42) of weight 4 with sign 0 over Rational Field
sage: S.is_cuspidal()
True
sage: S.cuspidal_submodule()
Modular Symbols subspace of dimension 40 of Modular Symbols space of dimension 48 for Gamma_0(42) of weight 4 with sign 0 over Rational Field
The cuspidal submodule of the cuspidal submodule is just itself:
sage: S.cuspidal_submodule() is S
True
sage: S.cuspidal_submodule() == S
True
An example where we abuse the _set_is_cuspidal function:
sage: M = ModularSymbols(389)
sage: S = M.eisenstein_submodule()
sage: S._set_is_cuspidal(True)
sage: S.cuspidal_submodule()
Modular Symbols subspace of dimension 1 of Modular Symbols space of dimension 65 for Gamma_0(389) of weight 2 with sign 0 over Rational Field
Return the diamond bracket d operator on this modular symbols space.
INPUT:
– integer
OUTPUT:
- matrix - the matrix of the diamond bracket operator on this space.
EXAMPLES:
sage: f = ModularSymbols(Gamma1(13),2,sign=1).cuspidal_subspace().decomposition()[0]
sage: a = f.diamond_bracket_operator(2).matrix()
sage: a.charpoly()
x^2 - x + 1
sage: a^12
[1 0]
[0 1]
Return the matrix of the dual star involution, which is induced by complex conjugation on the linear dual of modular symbols.
EXAMPLES:
sage: S = ModularSymbols(6,4) ; S.dual_star_involution_matrix()
[ 1 0 0 0 0 0]
[ 0 1 0 0 0 0]
[ 0 -2 1 2 0 0]
[ 0 2 0 -1 0 0]
[ 0 -2 0 2 1 0]
[ 0 2 0 -2 0 1]
sage: S.star_involution().matrix().transpose() == S.dual_star_involution_matrix()
True
Return the Eisenstein subspace of this space of modular symbols.
EXAMPLES:
sage: ModularSymbols(24,4).eisenstein_subspace()
Modular Symbols subspace of dimension 8 of Modular Symbols space of dimension 24 for Gamma_0(24) of weight 4 with sign 0 over Rational Field
sage: ModularSymbols(20,2).cuspidal_subspace().eisenstein_subspace()
Modular Symbols subspace of dimension 0 of Modular Symbols space of dimension 7 for Gamma_0(20) of weight 2 with sign 0 over Rational Field
Returns a list of pairs 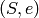 where
where  is simple
spaces of modular symbols and self is isomorphic to the direct sum
of the
is simple
spaces of modular symbols and self is isomorphic to the direct sum
of the 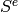 as a module over the anemic Hecke algebra
adjoin the star involution.
as a module over the anemic Hecke algebra
adjoin the star involution.
The cuspidal  are all simple, but the Eisenstein factors
need not be simple.
are all simple, but the Eisenstein factors
need not be simple.
The factors are sorted by dimension - don’t depend on much more for now.
ASSUMPTION: self is a module over the anemic Hecke algebra.
EXAMPLES: Note that if the sign is 1 then the cuspidal factors occur twice, one with each star eigenvalue.
sage: M = ModularSymbols(11)
sage: D = M.factorization(); D
(Modular Symbols subspace of dimension 1 of Modular Symbols space of dimension 3 for Gamma_0(11) of weight 2 with sign 0 over Rational Field) *
(Modular Symbols subspace of dimension 1 of Modular Symbols space of dimension 3 for Gamma_0(11) of weight 2 with sign 0 over Rational Field) *
(Modular Symbols subspace of dimension 1 of Modular Symbols space of dimension 3 for Gamma_0(11) of weight 2 with sign 0 over Rational Field)
sage: [A.T(2).matrix() for A, _ in D]
[[-2], [3], [-2]]
sage: [A.star_eigenvalues() for A, _ in D]
[[-1], [1], [1]]
In this example there is one old factor squared.
sage: M = ModularSymbols(22,sign=1)
sage: S = M.cuspidal_submodule()
sage: S.factorization()
(Modular Symbols subspace of dimension 1 of Modular Symbols space of dimension 2 for Gamma_0(11) of weight 2 with sign 1 over Rational Field)^2
sage: M = ModularSymbols(Gamma0(22), 2, sign=1)
sage: M1 = M.decomposition()[1]
sage: M1.factorization()
Modular Symbols subspace of dimension 3 of Modular Symbols space of dimension 5 for Gamma_0(22) of weight 2 with sign 1 over Rational Field
Compute the Hecke bound for self; that is, a number n such that the T_m for m = n generate the Hecke algebra.
EXAMPLES:
sage: M = ModularSymbols(24,8)
sage: M.hecke_bound()
53
sage: M.cuspidal_submodule().hecke_bound()
32
sage: M.eisenstein_submodule().hecke_bound()
53
Return True if self is cuspidal.
EXAMPLES:
sage: ModularSymbols(42,4).cuspidal_submodule().is_cuspidal()
True
sage: ModularSymbols(12,6).eisenstein_submodule().is_cuspidal()
False
Return True if self is an Eisenstein subspace.
EXAMPLES:
sage: ModularSymbols(22,6).cuspidal_submodule().is_eisenstein()
False
sage: ModularSymbols(22,6).eisenstein_submodule().is_eisenstein()
True
Return the star involution on self, which is induced by complex conjugation on modular symbols.
EXAMPLES:
sage: M = ModularSymbols(1,24)
sage: M.star_involution()
Hecke module morphism Star involution on Modular Symbols space of dimension 5 for Gamma_0(1) of weight 24 with sign 0 over Rational Field defined by the matrix
[ 1 0 0 0 0]
[ 0 -1 0 0 0]
[ 0 0 1 0 0]
[ 0 0 0 -1 0]
[ 0 0 0 0 1]
Domain: Modular Symbols space of dimension 5 for Gamma_0(1) of weight ...
Codomain: Modular Symbols space of dimension 5 for Gamma_0(1) of weight ...
sage: M.cuspidal_subspace().star_involution()
Hecke module morphism defined by the matrix
[ 1 0 0 0]
[ 0 -1 0 0]
[ 0 0 1 0]
[ 0 0 0 -1]
Domain: Modular Symbols subspace of dimension 4 of Modular Symbols space ...
Codomain: Modular Symbols subspace of dimension 4 of Modular Symbols space ...
sage: M.plus_submodule().star_involution()
Hecke module morphism defined by the matrix
[1 0 0]
[0 1 0]
[0 0 1]
Domain: Modular Symbols subspace of dimension 3 of Modular Symbols space ...
Codomain: Modular Symbols subspace of dimension 3 of Modular Symbols space ...
sage: M.minus_submodule().star_involution()
Hecke module morphism defined by the matrix
[-1 0]
[ 0 -1]
Domain: Modular Symbols subspace of dimension 2 of Modular Symbols space ...
Codomain: Modular Symbols subspace of dimension 2 of Modular Symbols space ...