Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Modular Symbols »
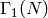 in
in 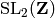 .¶
.¶A class representing a list of coset representatives for 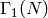 in
in
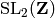 . What we actually calculate is a list of elements of
. What we actually calculate is a list of elements of
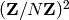 of exact order
of exact order  .
.
TESTS:
sage: L = sage.modular.modsym.g1list.G1list(18)
sage: loads(dumps(L)) == L
True
Return a list of vectors representing the cosets. Do not change the returned list!
EXAMPLE:
sage: L = sage.modular.modsym.g1list.G1list(4); L.list()
[(0, 1), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3), (2, 1), (2, 3), (3, 0), (3, 1), (3, 2), (3, 3)]
Given a pair 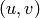 of integers, return the unique pair
of integers, return the unique pair 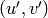 such that the pair
such that the pair 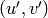 appears in self.list() and
appears in self.list() and 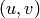 is equivalent to
is equivalent to 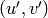 . This is rather trivial, but is here for
consistency with the P1List class which is the equivalent for
. This is rather trivial, but is here for
consistency with the P1List class which is the equivalent for
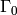 (where the problem is rather harder).
(where the problem is rather harder).
This will only make sense if  ; otherwise the
output will not be an element of self.
; otherwise the
output will not be an element of self.
EXAMPLE:
sage: L = sage.modular.modsym.g1list.G1list(4); L.normalize(6, 1)
(2, 1)
sage: L = sage.modular.modsym.g1list.G1list(4); L.normalize(6, 2) # nonsense!
(2, 2)