Compute spaces of half-integral weight modular forms.

Based on an algorithm in Basmaji’s thesis.

AUTHORS:

• William Stein (2007-08)

sage.modular.modform.half_integral.half_integral_weight_modform_basis(chi, k, prec)

A basis for the space of weight 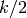forms with character 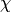. The modulus of 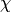must be divisible by 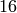and must be odd and .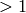

INPUT:

• chi - a Dirichlet character with modulus divisible by 16
• k - an odd integer = 1
• prec - a positive integer

OUTPUT: a list of power series

Warning

1. This code is very slow because it requests computation of a basis of modular forms for integral weight spaces, and that computation is still very slow.
2. If you give an input prec that is too small, then the output list of power series may be larger than the dimension of the space of half-integral forms.

EXAMPLES:

We compute some half-integral weight forms of level 16*7

sage: half_integral_weight_modform_basis(DirichletGroup(16*7).0^2,3,30)
[q - 2*q^2 - q^9 + 2*q^14 + 6*q^18 - 2*q^21 - 4*q^22 - q^25 + O(q^30),
 q^2 - q^14 - 3*q^18 + 2*q^22 + O(q^30),
 q^4 - q^8 - q^16 + q^28 + O(q^30),
 q^7 - 2*q^15 + O(q^30)]

The following illustrates that choosing too low of a precision can give an incorrect answer.

sage: half_integral_weight_modform_basis(DirichletGroup(16*7).0^2,3,20)
[q - 2*q^2 - q^9 + 2*q^14 + 6*q^18 + O(q^20),
 q^2 - q^14 - 3*q^18 + O(q^20),
 q^4 - 2*q^8 + 2*q^12 - 4*q^16 + O(q^20),
 q^7 - 2*q^8 + 4*q^12 - 2*q^15 - 6*q^16 + O(q^20),
 q^8 - 2*q^12 + 3*q^16 + O(q^20)]

We compute some spaces of low level and the first few possible weights.

sage: half_integral_weight_modform_basis(DirichletGroup(16,QQ).1, 3, 10)
[]
sage: half_integral_weight_modform_basis(DirichletGroup(16,QQ).1, 5, 10)
[q - 2*q^3 - 2*q^5 + 4*q^7 - q^9 + O(q^10)]
sage: half_integral_weight_modform_basis(DirichletGroup(16,QQ).1, 7, 10)
[q - 2*q^2 + 4*q^3 + 4*q^4 - 10*q^5 - 16*q^7 + 19*q^9 + O(q^10),
 q^2 - 2*q^3 - 2*q^4 + 4*q^5 + 4*q^7 - 8*q^9 + O(q^10),
 q^3 - 2*q^5 - 2*q^7 + 4*q^9 + O(q^10)]
sage: half_integral_weight_modform_basis(DirichletGroup(16,QQ).1, 9, 10)
[q - 2*q^2 + 4*q^3 - 8*q^4 + 14*q^5 + 16*q^6 - 40*q^7 + 16*q^8 - 57*q^9 + O(q^10),
 q^2 - 2*q^3 + 4*q^4 - 8*q^5 - 8*q^6 + 20*q^7 - 8*q^8 + 32*q^9 + O(q^10),
 q^3 - 2*q^4 + 4*q^5 + 4*q^6 - 10*q^7 - 16*q^9 + O(q^10),
 q^4 - 2*q^5 - 2*q^6 + 4*q^7 + 4*q^9 + O(q^10),
 q^5 - 2*q^7 - 2*q^9 + O(q^10)]

This example once raised an error (see trac #5792).

sage: half_integral_weight_modform_basis(trivial_character(16),9,10)
[q - 2*q^2 + 4*q^3 - 8*q^4 + 4*q^6 - 16*q^7 + 48*q^8 - 15*q^9 + O(q^10),
 q^2 - 2*q^3 + 4*q^4 - 2*q^6 + 8*q^7 - 24*q^8 + O(q^10),
 q^3 - 2*q^4 - 4*q^7 + 12*q^8 + O(q^10),
 q^4 - 6*q^8 + O(q^10)]

ALGORITHM: Basmaji (page 55 of his Essen thesis, “Ein Algorithmus zur Berechnung von Hecke-Operatoren und Anwendungen auf modulare Kurven”, http://wstein.org/scans/papers/basmaji/).

Let 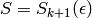be the space of cusp forms of even integer weight 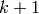and character 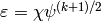, where 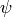is the nontrivial mod-4 Dirichlet character. Let 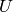be the subspace of 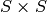of elements 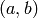such that 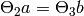. Then 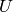is isomorphic to 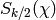via the map .
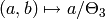