Graded Rings of Modular Forms¶

This module contains functions to find generators for the graded ring of modular forms of given level.

AUTHORS:

William Stein (2007-08-24): first version

class sage.modular.modform.find_generators.ModularFormsRing(group)¶

Bases: sage.structure.sage_object.SageObject

The ring of modular forms (of weights 0 or at least 2) for a congruence subgroup of 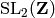${\rm SL}_2(\ZZ)$ .

EXAMPLES:

sage: ModularFormsRing(Gamma1(13))
Ring of modular forms for Congruence Subgroup Gamma1(13) of weights 0 and at least 2
sage: m = ModularFormsRing(4); m
Ring of modular forms for Congruence Subgroup Gamma0(4)
sage: m.modular_forms_of_weight(2)
Modular Forms space of dimension 2 for Congruence Subgroup Gamma0(4) of weight 2 over Rational Field
sage: m.modular_forms_of_weight(10)
Modular Forms space of dimension 6 for Congruence Subgroup Gamma0(4) of weight 10 over Rational Field
sage: m == loads(dumps(m))
True
sage: m.generators()
[(2, 1 + 24*q^2 + 24*q^4 + 96*q^6 + 24*q^8 + O(q^10)), 
(2, q + 4*q^3 + 6*q^5 + 8*q^7 + 13*q^9 + O(q^10))]
sage: m.q_expansion_basis(2,10)
[1 + 24*q^2 + 24*q^4 + 96*q^6 + 24*q^8 + O(q^10),
 q + 4*q^3 + 6*q^5 + 8*q^7 + 13*q^9 + O(q^10)]
sage: m.q_expansion_basis(3,10)
[]
sage: m.q_expansion_basis(10,10)
[1 + 10560*q^6 + 3960*q^8 + O(q^10),
 q - 8056*q^7 - 30855*q^9 + O(q^10),
 q^2 - 796*q^6 - 8192*q^8 + O(q^10),
 q^3 + 66*q^7 + 832*q^9 + O(q^10),
 q^4 + 40*q^6 + 528*q^8 + O(q^10),
 q^5 + 20*q^7 + 190*q^9 + O(q^10)]

generators(prec=10, maxweight=20)¶

Calculate modular forms generating a subring that contains all forms of weight up to maxweight (default 20).

EXAMPLES:

sage: ModularFormsRing(SL2Z).generators()
[(4, 1 + 240*q + 2160*q^2 + 6720*q^3 + 17520*q^4 + 30240*q^5 + 60480*q^6 + 82560*q^7 + 140400*q^8 + 181680*q^9 + O(q^10)), (6, 1 - 504*q - 16632*q^2 - 122976*q^3 - 532728*q^4 - 1575504*q^5 - 4058208*q^6 - 8471232*q^7 - 17047800*q^8 - 29883672*q^9 + O(q^10))]
sage: ModularFormsRing(SL2Z).generators(maxweight=5)
[(4, 1 + 240*q + 2160*q^2 + 6720*q^3 + 17520*q^4 + 30240*q^5 + 60480*q^6 + 82560*q^7 + 140400*q^8 + 181680*q^9 + O(q^10))]

modular_forms_of_weight(weight)¶

Return the space of modular forms on this group of the given weight.

EXAMPLES:

sage: R = ModularFormsRing(13)
sage: R.modular_forms_of_weight(10)
Modular Forms space of dimension 11 for Congruence Subgroup Gamma0(13) of weight 10 over Rational Field
sage: ModularFormsRing(Gamma1(13)).modular_forms_of_weight(3)
Modular Forms space of dimension 20 for Congruence Subgroup Gamma1(13) of weight 3 over Rational Field

q_expansion_basis(weight, prec=None)¶

Calculate a basis of q-expansions for the space of modular forms of the given weight for this group, calculated using the ring generators given by find_generators.

EXAMPLES:

sage: m = ModularFormsRing(Gamma0(4))
sage: m.q_expansion_basis(2,10)
[1 + 24*q^2 + 24*q^4 + 96*q^6 + 24*q^8 + O(q^10),
q + 4*q^3 + 6*q^5 + 8*q^7 + 13*q^9 + O(q^10)]
sage: m.q_expansion_basis(3,10)
[]

sage.modular.modform.find_generators.basis_for_modform_space(gens, group, weight)¶

Given a list of pairs (k,f) of a weight and a modular form of that weight, and a target weight l, return a basis of q-expansions for the weight l part of the graded algebra generated by those forms (which may or may not be the whole space of weight l forms for the given group).

EXAMPLES:

sage: X = ModularFormsRing(SL2Z).generators()
sage: sage.modular.modform.find_generators.basis_for_modform_space(X, SL2Z, 12)
[1 + 196560*q^2 + 16773120*q^3 + 398034000*q^4 + 4629381120*q^5 + 34417656000*q^6 + 187489935360*q^7 + 814879774800*q^8 + 2975551488000*q^9 + O(q^10), 
q - 24*q^2 + 252*q^3 - 1472*q^4 + 4830*q^5 - 6048*q^6 - 16744*q^7 + 84480*q^8 - 113643*q^9 + O(q^10)]

sage.modular.modform.find_generators.modform_generators(group, maxweight=20, prec=None, start_gens=[], start_weight=2)¶

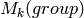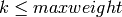Find modular forms in $M_k(group)$ for $k \leq maxweight$ , such that these forms generate – as an algebra – all forms on group of weight up to maxweight, where all forms are computed as $q$ -expansions to precision prec.

INPUT:

group – a level or a congruence subgroup
maxweight – integer
prec – integer (default: twice largest dimension)
start_gens – list of pairs (k,f) where k is an integer and f is a power series (default: []); if given, we assume the given pairs (k,f) are q-expansions of modular form of the given weight, and start creating modular forms generators using them.
start_weight – an integer (default: 2)

OUTPUT:

a list of pairs (k, f), where f is the q-expansion of a modular form of weight k.

EXAMPLES:

sage: import sage.modular.modform.find_generators as fg
sage: forms = [(4, 240*eisenstein_series_qexp(4,5)), (6,504*eisenstein_series_qexp(6,5))]
sage: fg.multiply_forms_to_weight(forms, 12)
[(12, 1 - 1008*q + 220752*q^2 + 16519104*q^3 + 399517776*q^4 + O(q^5)), (12, 1 + 720*q + 179280*q^2 + 16954560*q^3 + 396974160*q^4 + O(q^5))]
sage: fg.multiply_forms_to_weight(forms, 24)
[(24, 1 - 2016*q + 1457568*q^2 - 411997824*q^3 + 16227967392*q^4 + O(q^5)), (24, 1 - 288*q - 325728*q^2 + 11700864*q^3 + 35176468896*q^4 + O(q^5)), (24, 1 + 1440*q + 876960*q^2 + 292072320*q^3 + 57349833120*q^4 + O(q^5))]
sage: dimension_modular_forms(SL2Z,24)
3

sage: fg.modform_generators(1)
[(4, 1 + 240*q + 2160*q^2 + 6720*q^3 + O(q^4)), (6, 1 - 504*q - 16632*q^2 - 122976*q^3 + O(q^4))]
sage: fg.modform_generators(2)
[(2, 1 + 24*q + 24*q^2 + 96*q^3 + 24*q^4 + 144*q^5 + 96*q^6 + 192*q^7 + 24*q^8 + 312*q^9 + 144*q^10 + 288*q^11 + O(q^12)), (4, 1 + 240*q^2 + 2160*q^4 + 6720*q^6 + 17520*q^8 + 30240*q^10 + O(q^12))]
sage: fg.modform_generators(4, 12, 20)
[(2, 1 + 24*q^2 + 24*q^4 + 96*q^6 + 24*q^8 + 144*q^10 + 96*q^12 + 192*q^14 + 24*q^16 + 312*q^18 + O(q^20)), (2, q + 4*q^3 + 6*q^5 + 8*q^7 + 13*q^9 + 12*q^11 + 14*q^13 + 24*q^15 + 18*q^17 + 20*q^19 + O(q^20))]

Here we see that for \Gamma_0(11) taking a basis of forms in weights 2 and 4 is enough to generate everything up to weight 12 (and probably everything else).:

sage: v = fg.modform_generators(11, 12)
sage: len(v)
3
sage: [k for k, _ in v]
[2, 2, 4]
sage: dimension_modular_forms(11,2)
2
sage: dimension_modular_forms(11,4)
4    

For congruence subgroups not -1, we miss out some forms since we can’t calculate weight 1 forms at present, but we can still find generators for the ring of forms of weight 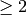$\ge 2$ :

sage: fg.modform_generators(Gamma1(4), prec=10, maxweight=10)
[(2, 1 + 24*q^2 + 24*q^4 + 96*q^6 + 24*q^8 + O(q^10)),
(2, q + 4*q^3 + 6*q^5 + 8*q^7 + 13*q^9 + O(q^10)),
(3, 1 + 12*q^2 + 64*q^3 + 60*q^4 + 160*q^6 + 384*q^7 + 252*q^8 + O(q^10)),
(3, q + 4*q^2 + 8*q^3 + 16*q^4 + 26*q^5 + 32*q^6 + 48*q^7 + 64*q^8 + 73*q^9 + O(q^10))]

sage.modular.modform.find_generators.multiply_forms_to_weight(forms, weight, stop_dim=None)¶

Given a list of pairs (k,f), where $k$ is an integer and $f$ is a power series, and a weight l, return all weight l forms obtained by multiplying together the given forms.

INPUT:

forms – list of pairs (k, f) with k an integer and f a power series
weight – an integer
stop_dim – integer (optional): if set to an integer and we find that the series so far span a space of at least this dimension, then stop multiplying more forms together.

EXAMPLES:

sage: import sage.modular.modform.find_generators as f
sage: forms = [(4, 240*eisenstein_series_qexp(4,5)), (6,504*eisenstein_series_qexp(6,5))]
sage: f.multiply_forms_to_weight(forms, 12)
[(12, 1 - 1008*q + 220752*q^2 + 16519104*q^3 + 399517776*q^4 + O(q^5)), (12, 1 + 720*q + 179280*q^2 + 16954560*q^3 + 396974160*q^4 + O(q^5))]
sage: f.multiply_forms_to_weight(forms, 24)
[(24, 1 - 2016*q + 1457568*q^2 - 411997824*q^3 + 16227967392*q^4 + O(q^5)), (24, 1 - 288*q - 325728*q^2 + 11700864*q^3 + 35176468896*q^4 + O(q^5)), (24, 1 + 1440*q + 876960*q^2 + 292072320*q^3 + 57349833120*q^4 + O(q^5))]
sage: dimension_modular_forms(SL2Z,24)
3

sage.modular.modform.find_generators.span_of_series(v, prec=None, basis=False)¶

Return the free module spanned by the given list of power series or objects with a padded_list method. If prec is not given, the precision used is the minimum of the precisions of the elements in the list (as determined by a prec method).

INPUT:

v – a list of power series
prec – optional; if given then the series do not have to be of finite precision, and will be considered to have precision prec.
basis – (default: False) if True the input is assumed to determine linearly independent vectors, and the resulting free module has that as basis.

OUTPUT:

A free module of rank prec over the base ring of the forms (actually, of the first form in the list). If the list is empty, the free module is over QQ.

EXAMPLES:

An example involving modular forms:

sage: from sage.modular.modform.find_generators import span_of_series
sage: v = ModularForms(11,2, prec=5).basis(); v
[
q - 2*q^2 - q^3 + 2*q^4 + O(q^5),
1 + 12/5*q + 36/5*q^2 + 48/5*q^3 + 84/5*q^4 + O(q^5)
]
sage: span_of_series(v)
Vector space of degree 5 and dimension 2 over Rational Field
Basis matrix:
[ 1  0 12 12 12]
[ 0  1 -2 -1  2]

Next we make sure the vectors give a basis:

sage: span_of_series(v,basis=True)
Vector space of degree 5 and dimension 2 over Rational Field
User basis matrix:
[   0    1   -2   -1    2]
[   1 12/5 36/5 48/5 84/5]

An example involving power series.:

sage: R.<x> = PowerSeriesRing(QQ, default_prec=5)
sage: v = [1/(1-x), 1/(1+x), 2/(1+x), 2/(1-x)]; v
[1 + x + x^2 + x^3 + x^4 + O(x^5),
 1 - x + x^2 - x^3 + x^4 + O(x^5),
 2 - 2*x + 2*x^2 - 2*x^3 + 2*x^4 + O(x^5),
 2 + 2*x + 2*x^2 + 2*x^3 + 2*x^4 + O(x^5)]
sage: span_of_series(v)
Vector space of degree 5 and dimension 2 over Rational Field
Basis matrix:
[1 0 1 0 1]
[0 1 0 1 0]
sage: span_of_series(v,10)
Vector space of degree 10 and dimension 2 over Rational Field
Basis matrix:
[1 0 1 0 1 0 0 0 0 0]
[0 1 0 1 0 0 0 0 0 0]

An example involving polynomials.:

sage: x = polygen(QQ)
sage: span_of_series([x^3, 2*x^2 + 17*x^3, x^2])
...
ValueError: please specify a precision
sage: span_of_series([x^3, 2*x^2 + 17*x^3, x^2],5)
Vector space of degree 5 and dimension 2 over Rational Field
Basis matrix:
[0 0 1 0 0]
[0 0 0 1 0]
sage: span_of_series([x^3, 2*x^2 + 17*x^3, x^2],3)
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[0 0 1]

Graded Rings of Modular Forms¶

Previous topic

Next topic

This Page

Navigation

Graded Rings of Modular Forms¶

Previous topic

Next topic

This Page

Quick search

Navigation