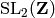The modular group

class sage.modular.arithgroup.congroup_sl2z.SL2Z_class

Bases: sage.modular.arithgroup.congroup_gamma0.Gamma0_class

The full modular group 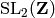, regarded as a congruence subgroup of itself.

is_subgroup(right)

Return True if self is a subgroup of right.

EXAMPLES:

sage: SL2Z.is_subgroup(SL2Z)
True
sage: SL2Z.is_subgroup(Gamma1(1))
True
sage: SL2Z.is_subgroup(Gamma0(6))
False

random_element(bound=100)

Return a random element of 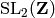with entries whose absolute value is strictly less than bound (default 100).

(Algorithm: Generate a random pair of integers at most bound. If they are not coprime, throw them away and start again. If they are, find an element of 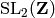whose bottom row is that, and left-multiply it by 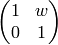for an integer 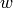randomly chosen from a small enough range that the answer still has entries at most bound.)

It is, unfortunately, not true that all elements of SL2Z with entries < bound appear with equal probability; those with larger bottom rows are favoured, because there are fewer valid possibilities for w.

EXAMPLES:

sage: SL2Z.random_element() # random
sage: SL2Z.random_element(5) # still random

reduce_cusp(c)

Return the unique reduced cusp equivalent to c under the action of self. Always returns Infinity, since there is only one equivalence class of cusps for .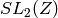

EXAMPLES:

sage: SL2Z.reduce_cusp(Cusps(-1/4))
Infinity

sage.modular.arithgroup.congroup_sl2z.is_SL2Z(x)

Return True if x is the modular group .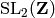

EXAMPLES:

sage: from sage.modular.arithgroup.all import is_SL2Z
sage: is_SL2Z(SL2Z)
True
sage: is_SL2Z(Gamma0(6))
False