Constructors for certain modular abelian varieties.

AUTHORS:

• William Stein (2007-03)

sage.modular.abvar.constructor.AbelianVariety(X)

Create the abelian variety corresponding to the given defining data.

INPUT:

• X - an integer, string, newform, modsym space, congruence subgroup or tuple of congruence subgroups

OUTPUT: a modular abelian variety

EXAMPLES:

sage: AbelianVariety(Gamma0(37))
Abelian variety J0(37) of dimension 2
sage: AbelianVariety('37a')
Newform abelian subvariety 37a of dimension 1 of J0(37)
sage: AbelianVariety(Newform('37a'))
Newform abelian subvariety 37a of dimension 1 of J0(37)
sage: AbelianVariety(ModularSymbols(37).cuspidal_submodule())
Abelian variety J0(37) of dimension 2
sage: AbelianVariety((Gamma0(37), Gamma0(11)))
Abelian variety J0(37) x J0(11) of dimension 3
sage: AbelianVariety(37)
Abelian variety J0(37) of dimension 2
sage: AbelianVariety([1,2,3])
...
TypeError: X must be an integer, string, newform, modsym space, congruence subgroup or tuple of congruence subgroups

sage.modular.abvar.constructor.J0(N)

Return the Jacobian 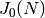of the modular curve .

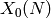EXAMPLES:

sage: J0(389)
Abelian variety J0(389) of dimension 32

The result is cached:

sage: J0(33) is J0(33)
True

sage.modular.abvar.constructor.J1(N)

Return the Jacobian 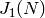of the modular curve .

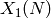EXAMPLES:

sage: J1(389)
Abelian variety J1(389) of dimension 6112

sage.modular.abvar.constructor.JH(N, H)

Return the Jacobian 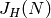of the modular curve .

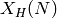EXAMPLES:

sage: JH(389,[2])
Abelian variety JH(389,[2]) of dimension 32