AUTHORS:
TESTS:
sage: A = J0(33)
sage: D = A.decomposition(); D
[
Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33),
Simple abelian subvariety 11a(3,33) of dimension 1 of J0(33),
Simple abelian subvariety 33a(1,33) of dimension 1 of J0(33)
]
sage: loads(dumps(D)) == D
True
sage: loads(dumps(A)) == A
True
Bases: sage.modular.abvar.abvar.ModularAbelianVariety_abstract
Return the lattice that defines this abelian variety.
OUTPUT:
EXAMPLES:
sage: A = (J0(11) * J0(37))[1]; A
Simple abelian subvariety 37a(1,37) of dimension 1 of J0(11) x J0(37)
sage: type(A)
<class 'sage.modular.abvar.abvar.ModularAbelianVariety_with_category'>
sage: A.lattice()
Free module of degree 6 and rank 2 over Integer Ring
Echelon basis matrix:
[ 0 0 1 -1 1 0]
[ 0 0 0 0 2 -1]
Bases: sage.structure.parent_base.ParentWithBase
Return the morphism from self to the ambient variety. This is injective if self is natural a subvariety of the ambient product Jacobian.
OUTPUT: morphism
The output is cached.
EXAMPLES: We compute the ambient structure morphism for an abelian
subvariety of 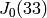 :
:
sage: A,B,C = J0(33)
sage: phi = A.ambient_morphism()
sage: phi.domain()
Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33)
sage: phi.codomain()
Abelian variety J0(33) of dimension 3
sage: phi.matrix()
[ 1 1 -2 0 2 -1]
[ 0 3 -2 -1 2 0]
phi is of course injective
sage: phi.kernel()
(Finite subgroup with invariants [] over QQ of Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33),
Abelian subvariety of dimension 0 of J0(33))
This is the same as the basis matrix for the lattice corresponding to self:
sage: A.lattice()
Free module of degree 6 and rank 2 over Integer Ring
Echelon basis matrix:
[ 1 1 -2 0 2 -1]
[ 0 3 -2 -1 2 0]
We compute a non-injective map to an ambient space:
sage: Q,pi = J0(33)/A
sage: phi = Q.ambient_morphism()
sage: phi.matrix()
[ 1 4 1 9 -1 -1]
[ 0 15 0 0 30 -75]
[ 0 0 5 10 -5 15]
[ 0 0 0 15 -15 30]
sage: phi.kernel()[0]
Finite subgroup with invariants [5, 15, 15] over QQ of Abelian variety factor of dimension 2 of J0(33)
Return the ambient modular abelian variety that contains this abelian variety. The ambient variety is always a product of Jacobians of modular curves.
OUTPUT: abelian variety
EXAMPLES:
sage: A = J0(33)[0]; A
Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33)
sage: A.ambient_variety()
Abelian variety J0(33) of dimension 3
EXAMPLES:
sage: A = J0(37); A
Abelian variety J0(37) of dimension 2
sage: A.base_extend(QQbar)
Abelian variety J0(37) over Algebraic Field of dimension 2
sage: A.base_extend(GF(7))
Abelian variety J0(37) over Finite Field of size 7 of dimension 2
Synonym for self.base_ring().
EXAMPLES:
sage: J0(11).base_field()
Rational Field
Change the base ring of this modular abelian variety.
EXAMPLES:
sage: A = J0(23)
sage: A.change_ring(QQ)
Abelian variety J0(23) of dimension 2
Return a complement of this abelian variety.
INPUT:
OUTPUT: abelian variety
EXAMPLES:
sage: a,b,c = J0(33)
sage: (a+b).complement()
Simple abelian subvariety 33a(1,33) of dimension 1 of J0(33)
sage: (a+b).complement() == c
True
sage: a.complement(a+b)
Abelian subvariety of dimension 1 of J0(33)
Return the cuspidal subgroup of this modular abelian variety. This is the subgroup generated by rational cusps.
EXAMPLES:
sage: J = J0(54)
sage: C = J.cuspidal_subgroup()
sage: C.gens()
[[(1/3, 0, 0, 0, 0, 1/3, 0, 2/3)], [(0, 1/3, 0, 0, 0, 2/3, 0, 1/3)], [(0, 0, 1/9, 1/9, 1/9, 1/9, 1/9, 2/9)], [(0, 0, 0, 1/3, 0, 1/3, 0, 0)], [(0, 0, 0, 0, 1/3, 1/3, 0, 1/3)], [(0, 0, 0, 0, 0, 0, 1/3, 2/3)]]
sage: C.invariants()
[3, 3, 3, 3, 3, 9]
sage: J1(13).cuspidal_subgroup()
Finite subgroup with invariants [19, 19] over QQ of Abelian variety J1(13) of dimension 2
sage: A = J0(33)[0]
sage: A.cuspidal_subgroup()
Finite subgroup with invariants [5] over QQ of Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33)
Return a sequence of abelian subvarieties of self that are all simple, have finite intersection and sum to self.
INPUT: simple- bool (default: True) if True, all factors are simple. If False, each factor returned is isogenous to a power of a simple and the simples in each factor are distinct.
EXAMPLES:
sage: m = ModularSymbols(11).cuspidal_submodule()
sage: d1 = m.degeneracy_map(33,1).matrix(); d3=m.degeneracy_map(33,3).matrix()
sage: w = ModularSymbols(33).submodule((d1 + d3).image(), check=False)
sage: A = w.abelian_variety(); A
Abelian subvariety of dimension 1 of J0(33)
sage: D = A.decomposition(); D
[
Simple abelian subvariety 11a(3,33) of dimension 1 of J0(33)
]
sage: D[0] == A
True
sage: B = A + J0(33)[0]; B
Abelian subvariety of dimension 2 of J0(33)
sage: dd = B.decomposition(simple=False); dd
[
Abelian subvariety of dimension 2 of J0(33)
]
sage: dd[0] == B
True
sage: dd = B.decomposition(); dd
[
Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33),
Simple abelian subvariety 11a(3,33) of dimension 1 of J0(33)
]
sage: sum(dd) == B
True
We decompose a product of two Jacobians:
sage: (J0(33) * J0(11)).decomposition()
[
Simple abelian subvariety 11a(1,11) of dimension 1 of J0(33) x J0(11),
Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33) x J0(11),
Simple abelian subvariety 11a(3,33) of dimension 1 of J0(33) x J0(11),
Simple abelian subvariety 33a(1,33) of dimension 1 of J0(33) x J0(11)
]
If this abelian variety is obtained via decomposition then it gets
labeled with the newform label along with some information about
degeneracy maps. In particular, the label ends in a pair
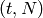 , where
, where  is the ambient level and
is the ambient level and
 is an integer that divides the quotient of
is an integer that divides the quotient of  by the newform level. This function returns the tuple
by the newform level. This function returns the tuple
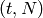 , or raises a ValueError if self isn’t simple.
, or raises a ValueError if self isn’t simple.
Note
It need not be the case that self is literally equal to the
image of the newform abelian variety under the 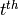 degeneracy map. See the documentation for the label method
for more details.
degeneracy map. See the documentation for the label method
for more details.
INPUT:
 , if it isn’t known. This None result is not cached.
, if it isn’t known. This None result is not cached.OUTPUT: a pair (integer, integer)
EXAMPLES:
sage: D = J0(33).decomposition(); D
[
Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33),
Simple abelian subvariety 11a(3,33) of dimension 1 of J0(33),
Simple abelian subvariety 33a(1,33) of dimension 1 of J0(33)
]
sage: D[0].degen_t()
(1, 33)
sage: D[1].degen_t()
(3, 33)
sage: D[2].degen_t()
(1, 33)
sage: J0(33).degen_t()
...
ValueError: self must be simple
Return the degeneracy map with domain self and given level/parameter. If self.ambient_variety() is a product of Jacobians (as opposed to a single Jacobian), then one can provide a list of new levels and parameters, corresponding to the ambient Jacobians in order. (See the examples below.)
INPUT:
 , or
, or ‘s.
‘s.OUTPUT: a degeneracy map
EXAMPLES: We make several degeneracy maps related to
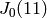 and
and 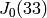 and compute their
matrices.
and compute their
matrices.
sage: d1 = J0(11).degeneracy_map(33, 1); d1
Degeneracy map from Abelian variety J0(11) of dimension 1 to Abelian variety J0(33) of dimension 3 defined by [1]
sage: d1.matrix()
[ 0 -3 2 1 -2 0]
[ 1 -2 0 1 0 -1]
sage: d2 = J0(11).degeneracy_map(33, 3); d2
Degeneracy map from Abelian variety J0(11) of dimension 1 to Abelian variety J0(33) of dimension 3 defined by [3]
sage: d2.matrix()
[-1 0 0 0 1 -2]
[-1 -1 1 -1 1 0]
sage: d3 = J0(33).degeneracy_map(11, 1); d3
Degeneracy map from Abelian variety J0(33) of dimension 3 to Abelian variety J0(11) of dimension 1 defined by [1]
He we verify that first mapping from level 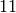 to level
to level
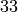 , then back is multiplication by
, then back is multiplication by 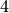 :
:
sage: d1.matrix() * d3.matrix()
[4 0]
[0 4]
We compute a more complicated degeneracy map involving nontrivial product ambient Jacobians; note that this is just the block direct sum of the two matrices at the beginning of this example:
sage: d = (J0(11)*J0(11)).degeneracy_map([33,33], [1,3]); d
Degeneracy map from Abelian variety J0(11) x J0(11) of dimension 2 to Abelian variety J0(33) x J0(33) of dimension 6 defined by [1, 3]
sage: d.matrix()
[ 0 -3 2 1 -2 0 0 0 0 0 0 0]
[ 1 -2 0 1 0 -1 0 0 0 0 0 0]
[ 0 0 0 0 0 0 -1 0 0 0 1 -2]
[ 0 0 0 0 0 0 -1 -1 1 -1 1 0]
Return the degree of this abelian variety, which is the dimension of the ambient Jacobian product.
EXAMPLES:
sage: A = J0(23)
sage: A.dimension()
2
Return the dimension of this abelian variety.
EXAMPLES:
sage: A = J0(23)
sage: A.dimension()
2
Compute the direct product of self and other.
INPUT:
OUTPUT: abelian variety
EXAMPLES:
sage: J0(11).direct_product(J1(13))
Abelian variety J0(11) x J1(13) of dimension 3
sage: A = J0(33)[0].direct_product(J0(33)[1]); A
Abelian subvariety of dimension 2 of J0(33) x J0(33)
sage: A.lattice()
Free module of degree 12 and rank 4 over Integer Ring
Echelon basis matrix:
[ 1 1 -2 0 2 -1 0 0 0 0 0 0]
[ 0 3 -2 -1 2 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 1 0 0 0 -1 2]
[ 0 0 0 0 0 0 0 1 -1 1 0 -2]
Return the dual of this abelian variety.
Warning
This is currently only implemented when self is an abelian subvariety of the ambient Jacobian product, and the complement of self in the ambient product Jacobian share no common factors. A more general implementation will require implementing computation of the intersection pairing on integral homology and the resulting Weil pairing on torsion.
EXAMPLES: We compute the dual of the elliptic curve newform abelian
variety of level 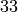 , and find the kernel of the modular
map, which has structure
, and find the kernel of the modular
map, which has structure 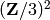 .
.
sage: A,B,C = J0(33)
sage: C
Simple abelian subvariety 33a(1,33) of dimension 1 of J0(33)
sage: Cd, f, pi = C.dual()
sage: f.matrix()
[3 0]
[0 3]
sage: f.kernel()[0]
Finite subgroup with invariants [3, 3] over QQ of Simple abelian subvariety 33a(1,33) of dimension 1 of J0(33)
By a theorem the modular degree must thus be 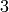 :
:
sage: E = EllipticCurve('33a')
sage: E.modular_degree()
3
Next we compute the dual of a  -dimensional new simple
abelian subvariety of
-dimensional new simple
abelian subvariety of 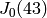 .
.
sage: A = AbelianVariety('43b'); A
Newform abelian subvariety 43b of dimension 2 of J0(43)
sage: Ad, f, pi = A.dual()
The kernel shows that the modular degree is  :
:
sage: f.kernel()[0]
Finite subgroup with invariants [2, 2] over QQ of Newform abelian subvariety 43b of dimension 2 of J0(43)
Unfortunately, the dual is not implemented in general:
sage: A = J0(22)[0]; A
Simple abelian subvariety 11a(1,22) of dimension 1 of J0(22)
sage: A.dual()
...
NotImplementedError: dual not implemented unless complement shares no simple factors with self.
Return the endomorphism ring of self.
OUTPUT: b = self.sturm_bound()
EXAMPLES: We compute a few endomorphism rings:
sage: J0(11).endomorphism_ring()
Endomorphism ring of Abelian variety J0(11) of dimension 1
sage: J0(37).endomorphism_ring()
Endomorphism ring of Abelian variety J0(37) of dimension 2
sage: J0(33)[2].endomorphism_ring()
Endomorphism ring of Simple abelian subvariety 33a(1,33) of dimension 1 of J0(33)
No real computation is done:
sage: J1(123456).endomorphism_ring()
Endomorphism ring of Abelian variety J1(123456) of dimension 423185857
Return a finite subgroup of this modular abelian variety.
INPUT:
OUTPUT: a finite subgroup of a modular abelian variety
EXAMPLES:
sage: J = J0(11)
sage: J.finite_subgroup([[1/5,0], [0,1/3]])
Finite subgroup with invariants [15] over QQbar of Abelian variety J0(11) of dimension 1
sage: J = J0(33); C = J[0].cuspidal_subgroup(); C
Finite subgroup with invariants [5] over QQ of Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33)
sage: J.finite_subgroup([[0,0,0,0,0,1/6]])
Finite subgroup with invariants [6] over QQbar of Abelian variety J0(33) of dimension 3
sage: J.finite_subgroup(C)
Finite subgroup with invariants [5] over QQ of Abelian variety J0(33) of dimension 3
Synonym for self.lattice().
OUTPUT: a free module over 
EXAMPLES:
sage: J0(37).free_module()
Ambient free module of rank 4 over the principal ideal domain Integer Ring
sage: J0(37)[0].free_module()
Free module of degree 4 and rank 2 over Integer Ring
Echelon basis matrix:
[ 1 -1 1 0]
[ 0 0 2 -1]
Return an ordered tuple of the congruence subgroups that the ambient product Jacobian is attached to.
Every modular abelian variety is a finite quotient of an abelian
subvariety of a product of modular Jacobians 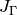 .
This function returns a tuple containing the groups
.
This function returns a tuple containing the groups
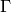 .
.
EXAMPLES:
sage: A = (J0(37) * J1(13))[0]; A
Simple abelian subvariety 13aG1(1,13) of dimension 2 of J0(37) x J1(13)
sage: A.groups()
(Congruence Subgroup Gamma0(37), Congruence Subgroup Gamma1(13))
Return the 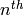 Hecke operator on the modular abelian
variety, if this makes sense [[elaborate]]. Otherwise raise a
ValueError.
Hecke operator on the modular abelian
variety, if this makes sense [[elaborate]]. Otherwise raise a
ValueError.
EXAMPLES: We compute 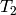 on
on 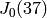 .
.
sage: t2 = J0(37).hecke_operator(2); t2
Hecke operator T_2 on Abelian variety J0(37) of dimension 2
sage: t2.charpoly().factor()
x * (x + 2)
sage: t2.index()
2
Note that there is no matrix associated to Hecke operators on modular abelian varieties. For a matrix, instead consider, e.g., the Hecke operator on integral or rational homology.
sage: t2.action_on_homology().matrix()
[-1 1 1 -1]
[ 1 -1 1 0]
[ 0 0 -2 1]
[ 0 0 0 0]
Return the characteristic polynomial of the 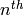 Hecke
operator
Hecke
operator 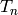 acting on self. Raises an ArithmeticError
if self is not Hecke equivariant.
acting on self. Raises an ArithmeticError
if self is not Hecke equivariant.
INPUT:
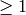
EXAMPLES:
sage: J0(33).hecke_polynomial(2)
x^3 + 3*x^2 - 4
sage: f = J0(33).hecke_polynomial(2, 'y'); f
y^3 + 3*y^2 - 4
sage: f.parent()
Univariate Polynomial Ring in y over Rational Field
sage: J0(33)[2].hecke_polynomial(3)
x + 1
sage: J0(33)[0].hecke_polynomial(5)
x - 1
sage: J0(33)[0].hecke_polynomial(11)
x - 1
sage: J0(33)[0].hecke_polynomial(3)
...
ArithmeticError: subspace is not invariant under matrix
Return the homology of this modular abelian variety.
Warning
For efficiency reasons the basis of the integral homology need not be the same as the basis for the rational homology.
EXAMPLES:
sage: J0(389).homology(GF(7))
Homology with coefficients in Finite Field of size 7 of Abelian variety J0(389) of dimension 32
sage: J0(389).homology(QQ)
Rational Homology of Abelian variety J0(389) of dimension 32
sage: J0(389).homology(ZZ)
Integral Homology of Abelian variety J0(389) of dimension 32
Return True if self and other are abelian subvarieties of the same ambient product Jacobian.
EXAMPLES:
sage: A,B,C = J0(33)
sage: A.in_same_ambient_variety(B)
True
sage: A.in_same_ambient_variety(J0(11))
False
Return the integral homology of this modular abelian variety.
EXAMPLES:
sage: H = J0(43).integral_homology(); H
Integral Homology of Abelian variety J0(43) of dimension 3
sage: H.rank()
6
sage: H = J1(17).integral_homology(); H
Integral Homology of Abelian variety J1(17) of dimension 5
sage: H.rank()
10
If you just ask for the rank of the homology, no serious calculations are done, so the following is fast:
sage: H = J0(50000).integral_homology(); H
Integral Homology of Abelian variety J0(50000) of dimension 7351
sage: H.rank()
14702
A product:
sage: H = (J0(11) * J1(13)).integral_homology()
sage: H.hecke_operator(2)
Hecke operator T_2 on Integral Homology of Abelian variety J0(11) x J1(13) of dimension 3
sage: H.hecke_operator(2).matrix()
[-2 0 0 0 0 0]
[ 0 -2 0 0 0 0]
[ 0 0 -2 0 -1 1]
[ 0 0 1 -1 0 -1]
[ 0 0 1 1 -2 0]
[ 0 0 0 1 -1 -1]
Returns the intersection of self and other inside a common ambient Jacobian product.
INPUT:
OUTPUT: If other is a modular abelian variety:
EXAMPLES: We intersect some abelian varieties with finite intersection.
sage: J = J0(37)
sage: J[0].intersection(J[1])
(Finite subgroup with invariants [2, 2] over QQ of Simple abelian subvariety 37a(1,37) of dimension 1 of J0(37), Simple abelian subvariety of dimension 0 of J0(37))
sage: D = list(J0(65)); D
[Simple abelian subvariety 65a(1,65) of dimension 1 of J0(65), Simple abelian subvariety 65b(1,65) of dimension 2 of J0(65), Simple abelian subvariety 65c(1,65) of dimension 2 of J0(65)]
sage: D[0].intersection(D[1])
(Finite subgroup with invariants [2] over QQ of Simple abelian subvariety 65a(1,65) of dimension 1 of J0(65), Simple abelian subvariety of dimension 0 of J0(65))
sage: (D[0]+D[1]).intersection(D[1]+D[2])
(Finite subgroup with invariants [2] over QQbar of Abelian subvariety of dimension 3 of J0(65), Abelian subvariety of dimension 2 of J0(65))
sage: J = J0(33)
sage: J[0].intersection(J[1])
(Finite subgroup with invariants [5] over QQ of Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33), Simple abelian subvariety of dimension 0 of J0(33))
Next we intersect two abelian varieties with non-finite intersection:
sage: J = J0(67); D = J.decomposition(); D
[
Simple abelian subvariety 67a(1,67) of dimension 1 of J0(67),
Simple abelian subvariety 67b(1,67) of dimension 2 of J0(67),
Simple abelian subvariety 67c(1,67) of dimension 2 of J0(67)
]
sage: (D[0] + D[1]).intersection(D[1] + D[2])
(Finite subgroup with invariants [5, 10] over QQbar of Abelian subvariety of dimension 3 of J0(67), Abelian subvariety of dimension 2 of J0(67))
Return True if self equals the ambient product Jacobian.
OUTPUT: bool
EXAMPLES:
sage: A,B,C = J0(33)
sage: A.is_ambient()
False
sage: J0(33).is_ambient()
True
sage: (A+B).is_ambient()
False
sage: (A+B+C).is_ambient()
True
Return True if self is stable under the Hecke operators of its ambient Jacobian.
OUTPUT: bool
EXAMPLES:
sage: J0(11).is_hecke_stable()
True
sage: J0(33)[2].is_hecke_stable()
True
sage: J0(33)[0].is_hecke_stable()
False
sage: (J0(33)[0] + J0(33)[1]).is_hecke_stable()
True
Return whether or not this modular abelian variety is simple, i.e., has no proper nonzero abelian subvarieties.
INPUT:
EXAMPLES:
sage: J0(5).is_simple(none_if_not_known=True) is None # this may fail if J0(5) comes up elsewhere...
True
sage: J0(33).is_simple()
False
sage: J0(33).is_simple(none_if_not_known=True)
False
sage: J0(33)[1].is_simple()
True
sage: J1(17).is_simple()
False
Return True if self is a subvariety of other as they sit in a common ambient modular Jacobian. In particular, this function will only return True if self and other have exactly the same ambient Jacobians.
EXAMPLES:
sage: J = J0(37); J
Abelian variety J0(37) of dimension 2
sage: A = J[0]; A
Simple abelian subvariety 37a(1,37) of dimension 1 of J0(37)
sage: A.is_subvariety(A)
True
sage: A.is_subvariety(J)
True
Return True if self is (presented as) a subvariety of the ambient product Jacobian.
Every abelian variety in Sage is a quotient of a subvariety of an ambient Jacobian product by a finite subgroup.
EXAMPLES:
sage: J0(33).is_subvariety_of_ambient_jacobian()
True
sage: A = J0(33)[0]; A
Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33)
sage: A.is_subvariety_of_ambient_jacobian()
True
sage: B, phi = A / A.torsion_subgroup(2)
sage: B
Abelian variety factor of dimension 1 of J0(33)
sage: phi.matrix()
[2 0]
[0 2]
sage: B.is_subvariety_of_ambient_jacobian()
False
Return the number (starting at 0) of the isogeny class of new simple abelian varieties that self is in. If self is not simple, raises a ValueError exception.
INPUT:
EXAMPLES: We test the none_if_not_known flag first:
sage: J0(33).isogeny_number(none_if_not_known=True) is None
True
Of course, 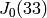 is not simple, so this function
raises a ValueError:
is not simple, so this function
raises a ValueError:
sage: J0(33).isogeny_number()
...
ValueError: self must be simple
Each simple factor has isogeny number 1, since that’s the number at which the factor is new.
sage: J0(33)[1].isogeny_number()
0
sage: J0(33)[2].isogeny_number()
0
Next consider 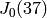 where there are two distinct
newform factors:
where there are two distinct
newform factors:
sage: J0(37)[1].isogeny_number()
1
Return the label associated to this modular abelian variety.
The format of the label is [level][isogeny class][group](t, ambient level)
If this abelian variety  has the above label, this
implies only that
has the above label, this
implies only that  is isogenous to the newform abelian
variety
is isogenous to the newform abelian
variety 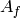 associated to the newform with label
[level][isogeny class][group]. The [group] is empty for
associated to the newform with label
[level][isogeny class][group]. The [group] is empty for
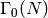 , is G1 for
, is G1 for 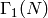 and is
GH[...] for
and is
GH[...] for 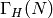 .
.
Warning
The sum of 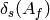 for all
for all 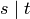 contains
contains  , but no sum for a proper divisor of
, but no sum for a proper divisor of
 contains
contains  . It need not be the case
that
. It need not be the case
that  is equal to
is equal to 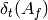 !!!
!!!
OUTPUT: string
EXAMPLES:
sage: J0(11).label()
'11a(1,11)'
sage: J0(11)[0].label()
'11a(1,11)'
sage: J0(33)[2].label()
'33a(1,33)'
sage: J0(22).label()
...
ValueError: self must be simple
We illustrate that self need not equal 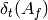 :
:
sage: J = J0(11); phi = J.degeneracy_map(33, 1) + J.degeneracy_map(33,3)
sage: B = phi.image(); B
Abelian subvariety of dimension 1 of J0(33)
sage: B.decomposition()
[
Simple abelian subvariety 11a(3,33) of dimension 1 of J0(33)
]
sage: C = J.degeneracy_map(33,3).image(); C
Abelian subvariety of dimension 1 of J0(33)
sage: C == B
False
Return lattice in ambient cuspidal modular symbols product that defines this modular abelian variety.
This must be defined in each derived class.
OUTPUT: a free module over 
EXAMPLES:
sage: A = sage.modular.abvar.abvar.ModularAbelianVariety_abstract((Gamma0(37),), QQ)
sage: A
...
NotImplementedError: BUG -- lattice method must be defined in derived class
Return the level of this modular abelian variety, which is an
integer N (usually minimal) such that this modular abelian variety
is a quotient of 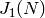 . In the case that the ambient
variety of self is a product of Jacobians, return the LCM of their
levels.
. In the case that the ambient
variety of self is a product of Jacobians, return the LCM of their
levels.
EXAMPLES:
sage: J1(5077).level()
5077
sage: JH(389,[4]).level()
389
sage: (J0(11)*J0(17)).level()
187
Return the complex  -series of this modular abelian
variety.
-series of this modular abelian
variety.
EXAMPLES:
sage: A = J0(37)
sage: A.lseries()
Complex L-series attached to Abelian variety J0(37) of dimension 2
Return the modular degree of this abelian variety, which is the square root of the degree of the modular kernel.
EXAMPLES:
sage: A = AbelianVariety('37a')
sage: A.modular_degree()
2
Return the modular kernel of this abelian variety, which is the kernel of the canonical polarization of self.
EXAMPLES:
sage: A = AbelianVariety('33a'); A
Newform abelian subvariety 33a of dimension 1 of J0(33)
sage: A.modular_kernel()
Finite subgroup with invariants [3, 3] over QQ of Newform abelian subvariety 33a of dimension 1 of J0(33)
Return the label [level][isogeny class][group] of the newform
 such that this abelian variety is isogenous to the
newform abelian variety
such that this abelian variety is isogenous to the
newform abelian variety 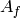 . If this abelian variety is
not simple, raise a ValueError.
. If this abelian variety is
not simple, raise a ValueError.
OUTPUT: string
EXAMPLES:
sage: J0(11).newform_label()
'11a'
sage: J0(33)[2].newform_label()
'33a'
The following fails since 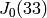 is not simple:
is not simple:
sage: J0(33).newform_label()
...
ValueError: self must be simple
Write self as a product (up to isogeny) of newform abelian
varieties 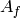 . Then this function return the least
common multiple of the levels of the newforms
. Then this function return the least
common multiple of the levels of the newforms  , along
with the corresponding group or list of groups (the groups do not
appear with multiplicity).
, along
with the corresponding group or list of groups (the groups do not
appear with multiplicity).
INPUT:
OUTPUT: integer group or list of distinct groups
EXAMPLES:
sage: J0(33)[0].newform_level()
(11, Congruence Subgroup Gamma0(33))
sage: J0(33)[0].newform_level(none_if_not_known=True)
(11, Congruence Subgroup Gamma0(33))
Here there are multiple groups since there are in fact multiple newforms:
sage: (J0(11) * J1(13)).newform_level()
(143, [Congruence Subgroup Gamma0(11), Congruence Subgroup Gamma1(13)])
Return the  -adic
-adic  -series of this modular
abelian variety.
-series of this modular
abelian variety.
EXAMPLES:
sage: A = J0(37)
sage: A.padic_lseries(7)
7-adic L-series attached to Abelian variety J0(37) of dimension 2
If self is an ambient product of Jacobians, return a projection from self to the nth such Jacobian.
EXAMPLES:
sage: J = J0(33)
sage: J.project_to_factor(0)
Abelian variety endomorphism of Abelian variety J0(33) of dimension 3
sage: J = J0(33) * J0(37) * J0(11)
sage: J.project_to_factor(2)
Abelian variety morphism:
From: Abelian variety J0(33) x J0(37) x J0(11) of dimension 6
To: Abelian variety J0(11) of dimension 1
sage: J.project_to_factor(2).matrix()
[0 0]
[0 0]
[0 0]
[0 0]
[0 0]
[0 0]
[0 0]
[0 0]
[0 0]
[0 0]
[1 0]
[0 1]
Given an abelian subvariety A of self, return a projection morphism from self to A. Note that this morphism need not be unique.
INPUT:
OUTPUT: a morphism
EXAMPLES:
sage: a,b,c = J0(33)
sage: pi = J0(33).projection(a); pi.matrix()
[ 3 -2]
[-5 5]
[-4 1]
[ 3 -2]
[ 5 0]
[ 1 1]
sage: pi = (a+b).projection(a); pi.matrix()
[ 0 0]
[-3 2]
[-4 1]
[-1 -1]
sage: pi = a.projection(a); pi.matrix()
[1 0]
[0 1]
We project onto a factor in a product of two Jacobians:
sage: A = J0(11)*J0(11); A
Abelian variety J0(11) x J0(11) of dimension 2
sage: A[0]
Simple abelian subvariety 11a(1,11) of dimension 1 of J0(11) x J0(11)
sage: A.projection(A[0])
Abelian variety morphism:
From: Abelian variety J0(11) x J0(11) of dimension 2
To: Simple abelian subvariety 11a(1,11) of dimension 1 of J0(11) x J0(11)
sage: A.projection(A[0]).matrix()
[0 0]
[0 0]
[1 0]
[0 1]
sage: A.projection(A[1]).matrix()
[1 0]
[0 1]
[0 0]
[0 0]
Return the group of all points of finite order in the algebraic closure of this abelian variety.
EXAMPLES:
sage: T = J0(33).qbar_torsion_subgroup(); T
Group of all torsion points in QQbar on Abelian variety J0(33) of dimension 3
The field of definition is the same as the base field of the abelian variety.
sage: T.field_of_definition()
Rational Field
On the other hand, T is a module over  .
.
sage: T.base_ring()
Integer Ring
Compute the quotient of self and other, where other is either an abelian subvariety of self or a finite subgroup of self.
INPUT:
OUTPUT: a pair (A, phi) with phi the quotient map from self to A
EXAMPLES: We quotient 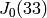 out by an abelian
subvariety:
out by an abelian
subvariety:
sage: Q, f = J0(33).quotient(J0(33)[0])
sage: Q
Abelian variety factor of dimension 2 of J0(33)
sage: f
Abelian variety morphism:
From: Abelian variety J0(33) of dimension 3
To: Abelian variety factor of dimension 2 of J0(33)
We quotient 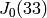 by the cuspidal subgroup:
by the cuspidal subgroup:
sage: C = J0(33).cuspidal_subgroup()
sage: Q, f = J0(33).quotient(C)
sage: Q
Abelian variety factor of dimension 3 of J0(33)
sage: f.kernel()[0]
Finite subgroup with invariants [10, 10] over QQ of Abelian variety J0(33) of dimension 3
sage: C
Finite subgroup with invariants [10, 10] over QQ of Abelian variety J0(33) of dimension 3
sage: J0(11).direct_product(J1(13))
Abelian variety J0(11) x J1(13) of dimension 3
Return the rank of the underlying lattice of self.
EXAMPLES:
sage: J = J0(33)
sage: J.rank()
6
sage: J[1]
Simple abelian subvariety 11a(3,33) of dimension 1 of J0(33)
sage: (J[1] * J[1]).rank()
4
Return the subgroup of this modular abelian variety generated by rational cusps.
This is a subgroup of the group of rational points in the cuspidal subgroup.
Warning
This is only currently implemented for
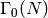 .
.
EXAMPLES:
sage: J = J0(54)
sage: CQ = J.rational_cusp_subgroup(); CQ
Finite subgroup with invariants [3, 3, 9] over QQ of Abelian variety J0(54) of dimension 4
sage: CQ.gens()
[[(1/3, 0, 0, 1/3, 2/3, 1/3, 0, 1/3)], [(0, 0, 1/9, 1/9, 7/9, 7/9, 1/9, 8/9)], [(0, 0, 0, 0, 0, 0, 1/3, 2/3)]]
sage: factor(CQ.order())
3^4
sage: CQ.invariants()
[3, 3, 9]
In this example the rational cuspidal subgroup and the cuspidal subgroup differ by a lot.
sage: J = J0(49)
sage: J.cuspidal_subgroup()
Finite subgroup with invariants [2, 14] over QQ of Abelian variety J0(49) of dimension 1
sage: J.rational_cusp_subgroup()
Finite subgroup with invariants [2] over QQ of Abelian variety J0(49) of dimension 1
Note that computation of the rational cusp subgroup isn’t
implemented for 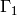 .
.
sage: J = J1(13)
sage: J.cuspidal_subgroup()
Finite subgroup with invariants [19, 19] over QQ of Abelian variety J1(13) of dimension 2
sage: J.rational_cusp_subgroup()
...
NotImplementedError: computation of rational cusps only implemented in Gamma0 case.
Return the rational subgroup of the cuspidal subgroup of this modular abelian variety.
This is a subgroup of the group of rational points in the cuspidal subgroup.
Warning
This is only currently implemented for
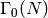 .
.
EXAMPLES:
sage: J = J0(54)
sage: CQ = J.rational_cuspidal_subgroup(); CQ
Finite subgroup with invariants [3, 3, 9] over QQ of Abelian variety J0(54) of dimension 4
sage: CQ.gens()
[[(1/3, 0, 0, 1/3, 2/3, 1/3, 0, 1/3)], [(0, 0, 1/9, 1/9, 7/9, 7/9, 1/9, 8/9)], [(0, 0, 0, 0, 0, 0, 1/3, 2/3)]]
sage: factor(CQ.order())
3^4
sage: CQ.invariants()
[3, 3, 9]
In this example the rational cuspidal subgroup and the cuspidal subgroup differ by a lot.
sage: J = J0(49)
sage: J.cuspidal_subgroup()
Finite subgroup with invariants [2, 14] over QQ of Abelian variety J0(49) of dimension 1
sage: J.rational_cuspidal_subgroup()
Finite subgroup with invariants [2] over QQ of Abelian variety J0(49) of dimension 1
Note that computation of the rational cusp subgroup isn’t
implemented for 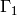 .
.
sage: J = J1(13)
sage: J.cuspidal_subgroup()
Finite subgroup with invariants [19, 19] over QQ of Abelian variety J1(13) of dimension 2
sage: J.rational_cuspidal_subgroup()
...
NotImplementedError: only implemented when group is Gamma0
Return the rational homology of this modular abelian variety.
EXAMPLES:
sage: H = J0(37).rational_homology(); H
Rational Homology of Abelian variety J0(37) of dimension 2
sage: H.rank()
4
sage: H.base_ring()
Rational Field
sage: H = J1(17).rational_homology(); H
Rational Homology of Abelian variety J1(17) of dimension 5
sage: H.rank()
10
sage: H.base_ring()
Rational Field
Return the maximal torsion subgroup of self defined over QQ.
EXAMPLES:
sage: J = J0(33)
sage: A = J.new_subvariety()
sage: A
Abelian subvariety of dimension 1 of J0(33)
sage: t = A.rational_torsion_subgroup()
sage: t.multiple_of_order()
4
sage: t.divisor_of_order()
4
sage: t.order()
4
sage: t.gens()
[[(1/2, 0, 0, -1/2, 0, 0)], [(0, 0, 1/2, 0, 1/2, -1/2)]]
sage: t
Torsion subgroup of Abelian subvariety of dimension 1 of J0(33)
Return the Shimura subgroup of this modular abelian variety. This is
the kernel of 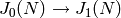 under the natural map.
Here we compute the Shimura subgroup as the kernel of
under the natural map.
Here we compute the Shimura subgroup as the kernel of
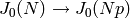 where the map is the difference between the
two degeneracy maps.
where the map is the difference between the
two degeneracy maps.
EXAMPLES:
sage: J=J0(11)
sage: J.shimura_subgroup()
Finite subgroup with invariants [5] over QQ of Abelian variety J0(11) of dimension 1
sage: J=J0(17)
sage: G=J.cuspidal_subgroup(); G
Finite subgroup with invariants [4] over QQ of Abelian variety J0(17) of dimension 1
sage: S=J.shimura_subgroup(); S
Finite subgroup with invariants [4] over QQ of Abelian variety J0(17) of dimension 1
sage: G.intersection(S)
Finite subgroup with invariants [2] over QQ of Abelian variety J0(17) of dimension 1
sage: J=J0(33)
sage: A=J.decomposition()[0]
sage: A.shimura_subgroup()
Finite subgroup with invariants [5] over QQ of Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33)
sage: J.shimura_subgroup()
Finite subgroup with invariants [10] over QQ of Abelian variety J0(33) of dimension 3
Return a bound  such that all Hecke operators
such that all Hecke operators
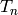 for
for 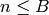 generate the Hecke algebra.
generate the Hecke algebra.
OUTPUT: integer
EXAMPLES:
sage: J0(11).sturm_bound()
2
sage: J0(33).sturm_bound()
8
sage: J1(17).sturm_bound()
48
sage: J1(123456).sturm_bound()
1693483008
sage: JH(37,[2,3]).sturm_bound()
7
sage: J1(37).sturm_bound()
228
If n is an integer, return the subgroup of points of order n.
Return the  -torsion subgroup of elements of order
dividing
-torsion subgroup of elements of order
dividing  of this modular abelian variety
of this modular abelian variety  ,
i.e., the group
,
i.e., the group ![A[n]](../../../_images/math/709d19d892be8f16edd309911617557ce0ae32a5.png) .
.
EXAMPLES:
sage: J1(13).torsion_subgroup(19)
Finite subgroup with invariants [19, 19, 19, 19] over QQ of Abelian variety J1(13) of dimension 2
sage: A = J0(23)
sage: G = A.torsion_subgroup(5); G
Finite subgroup with invariants [5, 5, 5, 5] over QQ of Abelian variety J0(23) of dimension 2
sage: G.order()
625
sage: G.gens()
[[(1/5, 0, 0, 0)], [(0, 1/5, 0, 0)], [(0, 0, 1/5, 0)], [(0, 0, 0, 1/5)]]
sage: A = J0(23)
sage: A.torsion_subgroup(2).order()
16
Return vector space corresponding to the modular abelian variety.
This is the lattice tensored with  .
.
EXAMPLES:
sage: J0(37).vector_space()
Vector space of dimension 4 over Rational Field
sage: J0(37)[0].vector_space()
Vector space of degree 4 and dimension 2 over Rational Field
Basis matrix:
[ 1 -1 0 1/2]
[ 0 0 1 -1/2]
Return the zero subgroup of this modular abelian variety, as a finite group.
EXAMPLES:
sage: A =J0(54); G = A.zero_subgroup(); G
Finite subgroup with invariants [] over QQ of Abelian variety J0(54) of dimension 4
sage: G.is_subgroup(A)
True
Return the zero subvariety of self.
EXAMPLES:
sage: J = J0(37)
sage: J.zero_subvariety()
Simple abelian subvariety of dimension 0 of J0(37)
sage: J.zero_subvariety().level()
37
sage: J.zero_subvariety().newform_level()
(1, [])
Bases: sage.modular.abvar.abvar.ModularAbelianVariety_modsym_abstract
Return the Brandt module at p that corresponds to self. This is the factor of the vector space on the ideal class set in an order of level N in the quaternion algebra ramified at p and infinity.
EXAMPLES:
sage: J0(43)[1].brandt_module(43)
Subspace of dimension 2 of Brandt module of dimension 4 of level 43 of weight 2 over Rational Field
sage: J0(43)[1].brandt_module(43).basis()
((1, 0, -1/2, -1/2), (0, 1, -1/2, -1/2))
sage: J0(43)[0].brandt_module(43).basis()
((0, 0, 1, -1),)
sage: J0(35)[0].brandt_module(5).basis()
((1, 0, -1, 0),)
sage: J0(35)[0].brandt_module(7).basis()
((1, -1, 1, -1),)
Return the order of the component group of the special fiber at p of the Neron model of self.
NOTE: For bad primes, this is only implemented when the group if Gamma0 and p exactly divides the level.
NOTE: the input abelian variety must be simple
ALGORITHM: See “Component Groups of Quotients of J0(N)” by Kohel and Stein. That paper is about optimal quotients; however, section 4.1 of Conrad-Stein “Component Groups of Purely Toric Quotients”, one sees that the component group of an optimal quotient is the same as the component group of its dual (which is the subvariety).
EXAMPLES:
sage: A = J0(37)[1]
sage: A.component_group_order(37)
3
sage: A = J0(43)[1]
sage: A.component_group_order(37)
1
sage: A.component_group_order(43)
7
sage: A = J0(23)[0]
sage: A.component_group_order(23)
11
Return the Tamagawa number of this abelian variety at p.
NOTE: For bad primes, this is only implemented when the group if Gamma0 and p exactly divides the level and Atkin-Lehner acts diagonally on this abelian variety (e.g., if this variety is new and simple). See the self.component_group command for more information.
NOTE: the input abelian variety must be simple
In cases where this function doesn’t work, consider using the self.tamagawa_number_bounds functions.
EXAMPLES:
sage: A = J0(37)[1]
sage: A.tamagawa_number(37)
3
sage: A = J0(43)[1]
sage: A.tamagawa_number(37)
1
sage: A.tamagawa_number(43)
7
sage: A = J0(23)[0]
sage: A.tamagawa_number(23)
11
Return a divisor and multiple of the Tamagawa number of self at p.
NOTE: the input abelian variety must be simple
EXAMPLES:
sage: A = J0(63).new_subvariety()[1]; A
Simple abelian subvariety 63b(1,63) of dimension 2 of J0(63)
sage: A.tamagawa_number_bounds(7)
(3, 3, ())
sage: A.tamagawa_number_bounds(3)
(1, 0, (2, 3, 5))
Bases: sage.modular.abvar.abvar.ModularAbelianVariety_abstract
Decompose this modular abelian variety as a product of abelian subvarieties, up to isogeny.
INPUT: simple- bool (default: True) if True, all factors are simple. If False, each factor returned is isogenous to a power of a simple and the simples in each factor are distinct.
EXAMPLES:
sage: J = J0(33)
sage: J.decomposition()
[
Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33),
Simple abelian subvariety 11a(3,33) of dimension 1 of J0(33),
Simple abelian subvariety 33a(1,33) of dimension 1 of J0(33)
]
sage: J1(17).decomposition()
[
Simple abelian subvariety 17aG1(1,17) of dimension 1 of J1(17),
Simple abelian subvariety 17bG1(1,17) of dimension 4 of J1(17)
]
Return the dimension of this modular abelian variety.
EXAMPLES:
sage: J0(37)[0].dimension()
1
sage: J0(43)[1].dimension()
2
sage: J1(17)[1].dimension()
4
Return the congruence subgroup associated that this modular abelian variety is associated to.
EXAMPLES:
sage: J0(13).group()
Congruence Subgroup Gamma0(13)
sage: J1(997).group()
Congruence Subgroup Gamma1(997)
sage: JH(37,[3]).group()
Congruence Subgroup Gamma_H(37) with H generated by [3]
sage: J0(37)[1].groups()
(Congruence Subgroup Gamma0(37),)
Return the tuple of groups associated to the modular symbols abelian variety. This is always a 1-tuple.
OUTPUT: tuple
EXAMPLES:
sage: A = ModularSymbols(33).cuspidal_submodule().abelian_variety(); A
Abelian variety J0(33) of dimension 3
sage: A.groups()
(Congruence Subgroup Gamma0(33),)
sage: type(A)
<class 'sage.modular.abvar.abvar.ModularAbelianVariety_modsym_with_category'>
Return True if this abelian variety attached to a modular symbols space space is attached to the cuspidal subspace of the ambient modular symbols space.
OUTPUT: bool
EXAMPLES:
sage: A = ModularSymbols(43).cuspidal_subspace().abelian_variety(); A
Abelian variety J0(43) of dimension 3
sage: A.is_ambient()
True
sage: type(A)
<class 'sage.modular.abvar.abvar.ModularAbelianVariety_modsym_with_category'>
sage: A = ModularSymbols(43).cuspidal_subspace()[1].abelian_variety(); A
Abelian subvariety of dimension 2 of J0(43)
sage: A.is_ambient()
False
Return True if self is a subvariety of other.
EXAMPLES:
sage: J = J0(37); J
Abelian variety J0(37) of dimension 2
sage: A = J[0]; A
Simple abelian subvariety 37a(1,37) of dimension 1 of J0(37)
sage: A.is_subvariety(J)
True
sage: A.is_subvariety(J0(11))
False
There may be a way to map  into
into 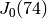 , but
, but
 is not equipped with any special structure of an
embedding.
is not equipped with any special structure of an
embedding.
sage: A.is_subvariety(J0(74))
False
Some ambient examples:
sage: J = J0(37)
sage: J.is_subvariety(J)
True
sage: J.is_subvariety(25)
False
More examples:
sage: A = J0(42); D = A.decomposition(); D
[
Simple abelian subvariety 14a(1,42) of dimension 1 of J0(42),
Simple abelian subvariety 14a(3,42) of dimension 1 of J0(42),
Simple abelian subvariety 21a(1,42) of dimension 1 of J0(42),
Simple abelian subvariety 21a(2,42) of dimension 1 of J0(42),
Simple abelian subvariety 42a(1,42) of dimension 1 of J0(42)
]
sage: D[0].is_subvariety(A)
True
sage: D[1].is_subvariety(D[0] + D[1])
True
sage: D[2].is_subvariety(D[0] + D[1])
False
Return the lattice the defines this modular symbols modular abelian variety.
OUTPUT: a free  -module embedded in an ambient
-module embedded in an ambient
 -vector space
-vector space
EXAMPLES:
sage: A = ModularSymbols(33).cuspidal_submodule()[0].abelian_variety(); A
Abelian subvariety of dimension 1 of J0(33)
sage: A.lattice()
Free module of degree 6 and rank 2 over Integer Ring
User basis matrix:
[ 1 0 0 -1 0 0]
[ 0 0 1 0 1 -1]
sage: type(A)
<class 'sage.modular.abvar.abvar.ModularAbelianVariety_modsym_with_category'>
Return space of modular symbols (with given sign) associated to this modular abelian variety, if it can be found by cutting down using Hecke operators. Otherwise raise a RuntimeError exception.
EXAMPLES:
sage: A = J0(37)
sage: A.modular_symbols()
Modular Symbols subspace of dimension 4 of Modular Symbols space of dimension 5 for Gamma_0(37) of weight 2 with sign 0 over Rational Field
sage: A.modular_symbols(1)
Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 3 for Gamma_0(37) of weight 2 with sign 1 over Rational Field
More examples:
sage: J0(11).modular_symbols()
Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 3 for Gamma_0(11) of weight 2 with sign 0 over Rational Field
sage: J0(11).modular_symbols(sign=1)
Modular Symbols subspace of dimension 1 of Modular Symbols space of dimension 2 for Gamma_0(11) of weight 2 with sign 1 over Rational Field
sage: J0(11).modular_symbols(sign=0)
Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 3 for Gamma_0(11) of weight 2 with sign 0 over Rational Field
sage: J0(11).modular_symbols(sign=-1)
Modular Symbols space of dimension 1 for Gamma_0(11) of weight 2 with sign -1 over Rational Field
Even more examples:
sage: A = J0(33)[1]; A
Simple abelian subvariety 11a(3,33) of dimension 1 of J0(33)
sage: A.modular_symbols()
Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 9 for Gamma_0(33) of weight 2 with sign 0 over Rational Field
It is not always possible to determine the sign subspaces:
sage: A.modular_symbols(1)
...
RuntimeError: unable to determine sign (=1) space of modular symbols
sage: A.modular_symbols(-1)
...
RuntimeError: unable to determine sign (=-1) space of modular symbols
Return the new or  -new subvariety of self.
-new subvariety of self.
INPUT:
EXAMPLES:
sage: J0(33).new_subvariety()
Abelian subvariety of dimension 1 of J0(33)
sage: J0(100).new_subvariety()
Abelian subvariety of dimension 1 of J0(100)
sage: J1(13).new_subvariety()
Abelian variety J1(13) of dimension 2
Return the old or  -old abelian variety of self.
-old abelian variety of self.
INPUT:
EXAMPLES:
sage: J0(33).old_subvariety()
Abelian subvariety of dimension 2 of J0(33)
sage: J0(100).old_subvariety()
Abelian subvariety of dimension 6 of J0(100)
sage: J1(13).old_subvariety()
Abelian subvariety of dimension 0 of J1(13)
Given an ambient modular symbols space, return complete factorization of it.
INPUT:
OUTPUT: list of decompositions corresponding to each new space.
EXAMPLES:
sage: M = ModularSymbols(33)
sage: sage.modular.abvar.abvar.factor_modsym_space_new_factors(M)
[[
Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 3 for Gamma_0(11) of weight 2 with sign 0 over Rational Field
],
[
Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 9 for Gamma_0(33) of weight 2 with sign 0 over Rational Field
]]
Given a new space  of modular symbols, return the
decomposition into simple of
of modular symbols, return the
decomposition into simple of  under the Hecke
operators.
under the Hecke
operators.
INPUT:
OUTPUT: list of factors
EXAMPLES:
sage: M = ModularSymbols(37).cuspidal_subspace()
sage: sage.modular.abvar.abvar.factor_new_space(M)
[
Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 5 for Gamma_0(37) of weight 2 with sign 0 over Rational Field,
Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 5 for Gamma_0(37) of weight 2 with sign 0 over Rational Field
]
Return True if x is a modular abelian variety.
INPUT:
EXAMPLES:
sage: from sage.modular.abvar.abvar import is_ModularAbelianVariety
sage: is_ModularAbelianVariety(5)
False
sage: is_ModularAbelianVariety(J0(37))
True
Returning True is a statement about the data type not whether or not some abelian variety is modular:
sage: is_ModularAbelianVariety(EllipticCurve('37a'))
False
Append lattice information to the output of simple_factorization_of_modsym_space.
INPUT:
OUTPUT: sequence with more information for each factor (the lattice)
EXAMPLES:
sage: M = ModularSymbols(33)
sage: factors = sage.modular.abvar.abvar.simple_factorization_of_modsym_space(M, simple=False)
sage: sage.modular.abvar.abvar.modsym_lattices(M, factors)
[
(11, 0, None, Modular Symbols subspace of dimension 4 of Modular Symbols space of dimension 9 for Gamma_0(33) of weight 2 with sign 0 over Rational Field, Free module of degree 6 and rank 4 over Integer Ring
Echelon basis matrix:
[ 1 0 0 0 -1 2]
[ 0 1 0 0 -1 1]
[ 0 0 1 0 -2 2]
[ 0 0 0 1 -1 -1]),
(33, 0, None, Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 9 for Gamma_0(33) of weight 2 with sign 0 over Rational Field, Free module of degree 6 and rank 2 over Integer Ring
Echelon basis matrix:
[ 1 0 0 -1 0 0]
[ 0 0 1 0 1 -1])
]
Return a random Hecke operator acting on  , got by adding
to
, got by adding
to  a random multiple of
a random multiple of 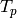
INPUT:
OUTPUT: Hecke operator prime
EXAMPLES:
sage: M = ModularSymbols(11).cuspidal_subspace()
sage: t, p = sage.modular.abvar.abvar.random_hecke_operator(M)
sage: p
3
sage: t, p = sage.modular.abvar.abvar.random_hecke_operator(M, t, p)
sage: p
5
Return factorization of  . If simple is False, return
powers of simples.
. If simple is False, return
powers of simples.
INPUT:
OUTPUT: sequence
EXAMPLES:
sage: M = ModularSymbols(33)
sage: sage.modular.abvar.abvar.simple_factorization_of_modsym_space(M)
[
(11, 0, 1, Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 9 for Gamma_0(33) of weight 2 with sign 0 over Rational Field),
(11, 0, 3, Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 9 for Gamma_0(33) of weight 2 with sign 0 over Rational Field),
(33, 0, 1, Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 9 for Gamma_0(33) of weight 2 with sign 0 over Rational Field)
]
sage: sage.modular.abvar.abvar.simple_factorization_of_modsym_space(M, simple=False)
[
(11, 0, None, Modular Symbols subspace of dimension 4 of Modular Symbols space of dimension 9 for Gamma_0(33) of weight 2 with sign 0 over Rational Field),
(33, 0, None, Modular Symbols subspace of dimension 2 of Modular Symbols space of dimension 9 for Gamma_0(33) of weight 2 with sign 0 over Rational Field)
]
Return the square root of the polynomial  .
.
Note
At some point something like this should be a member of the polynomial class. For now this is just used internally by some charpoly functions above.
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = (x-1)*(x+2)*(x^2 + 1/3*x + 5)
sage: f
x^4 + 4/3*x^3 + 10/3*x^2 + 13/3*x - 10
sage: sage.modular.abvar.abvar.sqrt_poly(f^2)
x^4 + 4/3*x^3 + 10/3*x^2 + 13/3*x - 10
sage: sage.modular.abvar.abvar.sqrt_poly(f)
...
ValueError: f must be a perfect square
sage: sage.modular.abvar.abvar.sqrt_poly(2*f^2)
...
ValueError: f must be monic