AUTHORS:
EXAMPLES:
sage: pari('5! + 10/x')
(120*x + 10)/x
sage: pari('intnum(x=0,13,sin(x)+sin(x^2) + x)')
85.1885681951527
sage: f = pari('x^3-1')
sage: v = f.factor(); v
[x - 1, 1; x^2 + x + 1, 1]
sage: v[0] # indexing is 0-based unlike in GP.
[x - 1, x^2 + x + 1]~
sage: v[1]
[1, 1]~
Arithmetic obeys the usual coercion rules.
sage: type(pari(1) + 1)
<type 'sage.libs.pari.gen.gen'>
sage: type(1 + pari(1))
<type 'sage.libs.pari.gen.gen'>
GUIDE TO REAL PRECISION AND THE PARI LIBRARY
The default real precision in communicating with the Pari library is the same as the default Sage real precision, which is 53 bits. Inexact Pari objects are therefore printed by default to 15 decimal digits (even if they are actually more precise).
Default precision example (53 bits, 15 significant decimals):
sage: a = pari(1.23); a
1.23000000000000
sage: a.sin()
0.942488801931698
Example with custom precision of 200 bits (60 significant decimals):
sage: R = RealField(200)
sage: a = pari(R(1.23)); a # only 15 significant digits printed
1.23000000000000
sage: R(a) # but the number is known to precision of 200 bits
1.2300000000000000000000000000000000000000000000000000000000
sage: a.sin() # only 15 significant digits printed
0.942488801931698
sage: R(a.sin()) # but the number is known to precision of 200 bits
0.94248880193169751002382356538924454146128740562765030213504
It is possible to change the number of printed decimals:
sage: R = RealField(200) # 200 bits of precision in computations
sage: old_prec = pari.set_real_precision(60) # 60 decimals printed
sage: a = pari(R(1.23)); a
1.23000000000000000000000000000000000000000000000000000000000
sage: a.sin()
0.942488801931697510023823565389244541461287405627650302135038
sage: pari.set_real_precision(old_prec) # restore the default printing behavior
60
Unless otherwise indicated in the docstring, most Pari functions that return inexact objects use the precision of their arguments to decide the precision of the computation. However, if some of these arguments happen to be exact numbers (integers, rationals, etc.), an optional parameter indicates the precision (in bits) to which these arguments should be converted before the computation. If this precision parameter is missing, the default precision of 53 bits is used. The following first converts 2 into a real with 53-bit precision:
sage: R = RealField()
sage: R(pari(2).sin())
0.909297426825682
We can ask for a better precision using the optional parameter:
sage: R = RealField(150)
sage: R(pari(2).sin(precision=150))
0.90929742682568169539601986591174484270225497
Warning regarding conversions Sage - Pari - Sage: Some care must be taken when juggling inexact types back and forth between Sage and Pari. In theory, calling p=pari(s) creates a Pari object p with the same precision as s; in practice, the Pari library’s precision is word-based, so it will go up to the next word. For example, a default 53-bit Sage real s will be bumped up to 64 bits by adding bogus 11 bits. The function p.python() returns a Sage object with exactly the same precision as the Pari object p. So pari(s).python() is definitely not equal to s, since it has 64 bits of precision, including the bogus 11 bits. The correct way of avoiding this is to coerce pari(s).python() back into a domain with the right precision. This has to be done by the user (or by Sage functions that use Pari library functions in gen.pyx). For instance, if we want to use the Pari library to compute sqrt(pi) with a precision of 100 bits:
sage: R = RealField(100)
sage: s = R(pi); s
3.1415926535897932384626433833
sage: p = pari(s).sqrt()
sage: x = p.python(); x # wow, more digits than I expected!
1.7724538509055160272981674833410973484
sage: x.prec() # has precision 'improved' from 100 to 128?
128
sage: x == RealField(128)(pi).sqrt() # sadly, no!
False
sage: R(x) # x should be brought back to precision 100
1.7724538509055160272981674833
sage: R(x) == s.sqrt()
True
Elliptic curves and precision: If you are working with elliptic curves and want to compute with a precision other than the default 53 bits, you should use the precision parameter of ellinit():
sage: R = RealField(150)
sage: e = pari([0,0,0,-82,0]).ellinit(precision=150)
sage: eta1 = e.elleta()[0]
sage: R(eta1)
3.6054636014326520863839536934492002728802618
Number fields and precision: TODO
Bases: sage.structure.parent_base.ParentWithBase
Return Euler’s constant to the requested real precision (in bits).
EXAMPLES:
sage: pari.euler()
0.577215664901533
sage: pari.euler(precision=100).python()
0.577215664901532860606512090082...
Return the factorial of the integer n as a PARI gen.
EXAMPLES:
sage: pari.factorial(0)
1
sage: pari.factorial(1)
1
sage: pari.factorial(5)
120
sage: pari.factorial(25)
15511210043330985984000000
Returns the current PARI default real precision.
This is used both for creation of new objects from strings and for printing. It is the number of digits IN DECIMAL in which real numbers are printed. It also determines the precision of objects created by parsing strings (e.g. pari(‘1.2’)), which is not the normal way of creating new pari objects in Sage. It has no effect on the precision of computations within the pari library.
Returns Pari’s current random number seed.
EXAMPLES:
sage: pari.setrand(50)
sage: pari.getrand()
50
sage: pari.pari_rand31()
621715893
sage: pari.getrand()
621715893
Recompute the primes table including at least all primes up to M (but possibly more).
EXAMPLES:
sage: pari.init_primes(200000)
listcreate(n): return an empty pari list of maximal length n.
EXAMPLES:
sage: pari.listcreate(20)
List([])
Returns a random number from Pari’s random number generator.
Return the value of the constant pi to the requested real precision (in bits).
EXAMPLES:
sage: pari.pi()
3.14159265358979
sage: pari.pi(precision=100).python()
3.1415926535897932384626433832...
polcyclo(n, v=x): cyclotomic polynomial of degree n, in variable v.
EXAMPLES:
sage: pari.polcyclo(8)
x^4 + 1
sage: pari.polcyclo(7, 'z')
z^6 + z^5 + z^4 + z^3 + z^2 + z + 1
sage: pari.polcyclo(1)
x - 1
pollegendre(n, v=x): Legendre polynomial of degree n (n C-integer), in variable v.
EXAMPLES:
sage: pari.pollegendre(7)
429/16*x^7 - 693/16*x^5 + 315/16*x^3 - 35/16*x
sage: pari.pollegendre(7, 'z')
429/16*z^7 - 693/16*z^5 + 315/16*z^3 - 35/16*z
sage: pari.pollegendre(0)
1
polsubcyclo(n, d, v=x): return the pari list of polynomial(s)
defining the sub-abelian extensions of degree  of the
cyclotomic field
of the
cyclotomic field 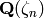 , where
, where  divides
divides 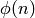 .
.
EXAMPLES:
sage: pari.polsubcyclo(8, 4)
[x^4 + 1]
sage: pari.polsubcyclo(8, 2, 'z')
[z^2 - 2, z^2 + 1, z^2 + 2]
sage: pari.polsubcyclo(8, 1)
[x - 1]
sage: pari.polsubcyclo(8, 3)
[]
poltchebi(n, v=x): Chebyshev polynomial of the first kind of degree n, in variable v.
EXAMPLES:
sage: pari.poltchebi(7)
64*x^7 - 112*x^5 + 56*x^3 - 7*x
sage: pari.poltchebi(7, 'z')
64*z^7 - 112*z^5 + 56*z^3 - 7*z
sage: pari.poltchebi(0)
1
prime_list(n): returns list of the first n primes
To extend the table of primes use pari.init_primes(M).
INPUT:
OUTPUT:
EXAMPLES:
sage: pari.prime_list(0)
[]
sage: pari.prime_list(-1)
[]
sage: pari.prime_list(3)
[2, 3, 5]
sage: pari.prime_list(10)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
sage: pari.prime_list(20)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71]
sage: len(pari.prime_list(1000))
1000
Return the primes <= n as a pari list.
EXAMPLES:
sage: pari.primes_up_to_n(1)
[]
sage: pari.primes_up_to_n(20)
[2, 3, 5, 7, 11, 13, 17, 19]
Read a script from the named filename into the interpreter, where s is a string. The functions defined in the script are then available for use from Sage/PARI.
EXAMPLE:
If foo.gp is a script that contains
{foo(n) =
n^2
}
and you type read("foo.gp"), then the command pari("foo(12)") will create the Python/PARI gen which is the integer 144.
CONSTRAINTS: The PARI script must not contain the following function calls:
print, default, ??? (please report any others that cause trouble)
Sets the PARI default real precision.
This is used both for creation of new objects from strings and for printing. It is the number of digits IN DECIMAL in which real numbers are printed. It also determines the precision of objects created by parsing strings (e.g. pari(‘1.2’)), which is not the normal way of creating new pari objects in Sage. It has no effect on the precision of computations within the pari library.
Returns the previous PARI real precision.
Sets Pari’s current random number seed.
This should not be called directly; instead, use Sage’s global random number seed handling in sage.misc.randstate and call current_randstate().set_seed_pari().
EXAMPLES:
sage: pari.setrand(12345)
sage: pari.getrand()
12345
vector(long n, entries=None): Create and return the length n PARI vector with given list of entries.
EXAMPLES:
sage: pari.vector(5, [1, 2, 5, 4, 3])
[1, 2, 5, 4, 3]
sage: pari.vector(2, [x, 1])
[x, 1]
sage: pari.vector(2, [x, 1, 5])
...
IndexError: length of entries (=3) must equal n (=2)
Bases: sage.structure.element.RingElement
Python extension class that models the PARI GEN type.
Col(x): Transforms the object x into a column vector.
The vector will have only one component, except in the following cases:
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari(1.5).Col()
[1.50000000000000]~
sage: pari([1,2,3,4]).Col()
[1, 2, 3, 4]~
sage: pari('[1,2; 3,4]').Col()
[[1, 2], [3, 4]]~
sage: pari('"Sage"').Col()
["S", "a", "g", "e"]~
sage: pari('3*x^3 + x').Col()
[3, 0, 1, 0]~
sage: pari('x + 3*x^3 + O(x^5)').Col()
[1, 0, 3, 0]~
List(x): transforms the PARI vector or list x into a list.
EXAMPLES:
sage: v = pari([1,2,3])
sage: v
[1, 2, 3]
sage: v.type()
't_VEC'
sage: w = v.List()
sage: w
List([1, 2, 3])
sage: w.type()
't_LIST'
Mat(x): Returns the matrix defined by x.
INPUT:
OUTPUT:
EXAMPLES:
sage: x = pari(5)
sage: x.type()
't_INT'
sage: y = x.Mat()
sage: y
Mat(5)
sage: y.type()
't_MAT'
sage: x = pari('[1,2;3,4]')
sage: x.type()
't_MAT'
sage: x = pari('[1,2,3,4]')
sage: x.type()
't_VEC'
sage: y = x.Mat()
sage: y
Mat([1, 2, 3, 4])
sage: y.type()
't_MAT'
sage: v = pari('[1,2;3,4]').Vec(); v
[[1, 3]~, [2, 4]~]
sage: v.Mat()
[1, 2; 3, 4]
sage: v = pari('[1,2;3,4]').Col(); v
[[1, 2], [3, 4]]~
sage: v.Mat()
[1, 2; 3, 4]
Mod(x, y): Returns the object x modulo y, denoted Mod(x, y).
The input y must be a an integer or a polynomial:
Warning
This function is not the same as x % y which is an integer or a polynomial.
INPUT:
OUTPUT:
EXAMPLES:
sage: z = pari(3)
sage: x = z.Mod(pari(7))
sage: x
Mod(3, 7)
sage: x^2
Mod(2, 7)
sage: x^100
Mod(4, 7)
sage: x.type()
't_INTMOD'
sage: f = pari("x^2 + x + 1")
sage: g = pari("x")
sage: a = g.Mod(f)
sage: a
Mod(x, x^2 + x + 1)
sage: a*a
Mod(-x - 1, x^2 + x + 1)
sage: a.type()
't_POLMOD'
Pol(x, v): convert x into a polynomial with main variable v and return the result.
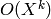 .
.Warning
This is not a substitution function. It will not transform an object containing variables of higher priority than v:
sage: pari('x+y').Pol('y')
...
PariError: (8)
INPUT:
OUTPUT:
EXAMPLES:
sage: v = pari("[1,2,3,4]")
sage: f = v.Pol()
sage: f
x^3 + 2*x^2 + 3*x + 4
sage: f*f
x^6 + 4*x^5 + 10*x^4 + 20*x^3 + 25*x^2 + 24*x + 16
sage: v = pari("[1,2;3,4]")
sage: v.Pol()
[1, 3]~*x + [2, 4]~
Polrev(x, v): Convert x into a polynomial with main variable v and return the result. This is the reverse of Pol if x is a vector, otherwise it is identical to Pol. By “reverse” we mean that the coefficients are reversed.
INPUT:
OUTPUT:
EXAMPLES:
sage: v = pari("[1,2,3,4]")
sage: f = v.Polrev()
sage: f
4*x^3 + 3*x^2 + 2*x + 1
sage: v.Pol()
x^3 + 2*x^2 + 3*x + 4
sage: v.Polrev('y')
4*y^3 + 3*y^2 + 2*y + 1
Note that Polrev does not reverse the coefficients of a polynomial!
sage: f
4*x^3 + 3*x^2 + 2*x + 1
sage: f.Polrev()
4*x^3 + 3*x^2 + 2*x + 1
sage: v = pari("[1,2;3,4]")
sage: v.Polrev()
[2, 4]~*x + [1, 3]~
Qfb(a,b,c,D=0.): Returns the binary quadratic form
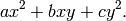
The optional D is 0 by default and initializes Shank’s distance if
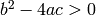 .
.
Note
Negative definite forms are not implemented, so use their positive definite counterparts instead. (I.e., if f is a negative definite quadratic form, then -f is positive definite.)
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(3).Qfb(7, 2)
Qfb(3, 7, 2, 0.E-19)
Ser(x,v=x): Create a power series from x with main variable v and return the result.
Warning
This is not a substitution function. It will not transform an object containing variables of higher priority than v.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(2).Ser()
2 + O(x^16)
sage: x = pari([1,2,3,4,5])
sage: x.Ser()
1 + 2*x + 3*x^2 + 4*x^3 + 5*x^4 + O(x^5)
sage: f = x.Ser('v'); print f
1 + 2*v + 3*v^2 + 4*v^3 + 5*v^4 + O(v^5)
sage: pari(1)/f
1 - 2*v + v^2 + O(v^5)
sage: pari(1).Ser()
1 + O(x^16)
Set(x): convert x into a set, i.e. a row vector of strings in increasing lexicographic order.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari([1,5,2]).Set()
["1", "2", "5"]
sage: pari([]).Set() # the empty set
[]
sage: pari([1,1,-1,-1,3,3]).Set()
["-1", "1", "3"]
sage: pari(1).Set()
["1"]
sage: pari('1/(x*y)').Set()
["1/(y*x)"]
sage: pari('["bc","ab","bc"]').Set()
["ab", "bc"]
Str(self): Return the print representation of self as a PARI object.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari([1,2,['abc',1]]).Str()
[1, 2, [abc, 1]]
sage: pari([1,1, 1.54]).Str()
[1, 1, 1.54000000000000]
sage: pari(1).Str() # 1 is automatically converted to string rep
1
sage: x = pari('x') # PARI variable "x"
sage: x.Str() # is converted to string rep.
x
sage: x.Str().type()
't_STR'
Strchr(x): converts x to a string, translating each integer into a character (in ASCII).
Note
Vecsmall() is (essentially) the inverse to Strchr().
INPUT:
OUTPUT:
EXAMPLES:
sage: pari([65,66,123]).Strchr()
AB{
sage: pari('"Sage"').Vecsmall() # pari('"Sage"') --> PARI t_STR
Vecsmall([83, 97, 103, 101])
sage: _.Strchr()
Sage
sage: pari([83, 97, 103, 101]).Strchr()
Sage
Strexpand(x): Concatenate the entries of the vector x into a single string, performing tilde expansion.
Note
I have no clue what the point of this function is. - William
Strtex(x): Translates the vector x of PARI gens to TeX format and returns the resulting concatenated strings as a PARI t_STR.
INPUT:
OUTPUT:
EXAMPLES:
sage: v=pari('x^2')
sage: v.Strtex()
x^2
sage: v=pari(['1/x^2','x'])
sage: v.Strtex()
\frac{1}{x^2}x
sage: v=pari(['1 + 1/x + 1/(y+1)','x-1'])
sage: v.Strtex()
\frac{ \left(y
+ 2\right) x
+ \left(y
+ 1\right) }{ \left(y
+ 1\right) x}x
- 1
Vec(x): Transforms the object x into a vector.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(1).Vec()
[1]
sage: pari('x^3').Vec()
[1, 0, 0, 0]
sage: pari('x^3 + 3*x - 2').Vec()
[1, 0, 3, -2]
sage: pari([1,2,3]).Vec()
[1, 2, 3]
sage: pari('ab').Vec()
[1, 0]
Vecrev(x): Transforms the object x into a vector. Identical to Vec(x) except when x is - a polynomial, this is the reverse of Vec. - a power series, this includes low-order zero coefficients. - a Laurent series, raises an exception
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(1).Vecrev()
[1]
sage: pari('x^3').Vecrev()
[0, 0, 0, 1]
sage: pari('x^3 + 3*x - 2').Vecrev()
[-2, 3, 0, 1]
sage: pari([1, 2, 3]).Vecrev()
[1, 2, 3]
sage: pari('Col([1, 2, 3])').Vecrev()
[1, 2, 3]
sage: pari('[1, 2; 3, 4]').Vecrev()
[[1, 3]~, [2, 4]~]
sage: pari('ab').Vecrev()
[0, 1]
sage: pari('x^2 + 3*x^3 + O(x^5)').Vecrev()
[0, 0, 1, 3, 0]
sage: pari('x^-2 + 3*x^3 + O(x^5)').Vecrev()
...
ValueError: Vecrev() is not defined for Laurent series
Vecsmall(x): transforms the object x into a t_VECSMALL.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari([1,2,3]).Vecsmall()
Vecsmall([1, 2, 3])
sage: pari('"Sage"').Vecsmall()
Vecsmall([83, 97, 103, 101])
sage: pari(1234).Vecsmall()
Vecsmall([1234])
Returns the absolute value of x (its modulus, if x is complex). Rational functions are not allowed. Contrary to most transcendental functions, an exact argument is not converted to a real number before applying abs and an exact result is returned if possible.
EXAMPLES:
sage: x = pari("-27.1")
sage: x.abs()
27.1000000000000
If x is a polynomial, returns -x if the leading coefficient is real and negative else returns x. For a power series, the constant coefficient is considered instead.
EXAMPLES:
sage: pari('x-1.2*x^2').abs()
1.20000000000000*x^2 - x
The principal branch of 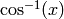 , so that
, so that
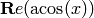 belongs to
belongs to ![[0,Pi]](../../../_images/math/6786c32c3f635f7bc5a4e38491d9f94948f8bf49.png) . If
. If  is real and
is real and 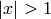 , then
, then 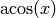 is complex.
is complex.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(0.5).acos()
1.04719755119660
sage: pari(1/2).acos()
1.04719755119660
sage: pari(1.1).acos()
-0.443568254385115*I
sage: C.<i> = ComplexField()
sage: pari(1.1+i).acos()
0.849343054245252 - 1.09770986682533*I
The principal branch of 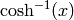 , so that
, so that
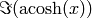 belongs to
belongs to ![[0,Pi]](../../../_images/math/6786c32c3f635f7bc5a4e38491d9f94948f8bf49.png) . If
. If
 is real and
is real and 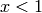 , then
, then
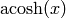 is complex.
is complex.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(2).acosh()
1.31695789692482
sage: pari(0).acosh()
1.57079632679490*I
sage: C.<i> = ComplexField()
sage: pari(i).acosh()
0.881373587019543 + 1.57079632679490*I
The arithmetic-geometric mean of x and y. In the case of complex or negative numbers, the principal square root is always chosen. p-adic or power series arguments are also allowed. Note that a p-adic AGM exists only if x/y is congruent to 1 modulo p (modulo 16 for p=2). x and y cannot both be vectors or matrices.
If any of  or
or  is an exact argument, it is
first converted to a real or complex number using the optional
parameter precision (in bits). If the arguments are inexact (e.g.
real), the smallest of their two precisions is used in the
computation, and the parameter precision is ignored.
is an exact argument, it is
first converted to a real or complex number using the optional
parameter precision (in bits). If the arguments are inexact (e.g.
real), the smallest of their two precisions is used in the
computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(2).agm(2)
2.00000000000000
sage: pari(0).agm(1)
0
sage: pari(1).agm(2)
1.45679103104691
sage: C.<i> = ComplexField()
sage: pari(1+i).agm(-3)
-0.964731722290876 + 1.15700282952632*I
EXAMPLES:
sage: n = pari.set_real_precision (200)
sage: w1 = pari('z1=2-sqrt(26); (z1+I)/(z1-I)')
sage: f = w1.algdep(12); f
545*x^11 - 297*x^10 - 281*x^9 + 48*x^8 - 168*x^7 + 690*x^6 - 168*x^5 + 48*x^4 - 281*x^3 - 297*x^2 + 545*x
sage: f(w1)
7.75513996 E-200 + 5.70672991 E-200*I # 32-bit
3.780069700150794274 E-209 - 9.362977321012524836 E-211*I # 64-bit
sage: f.factor()
[x, 1; x + 1, 2; x^2 + 1, 1; x^2 + x + 1, 1; 545*x^4 - 1932*x^3 + 2790*x^2 - 1932*x + 545, 1]
sage: pari.set_real_precision(n)
200
arg(x): argument of x,such that 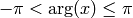 .
.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: C.<i> = ComplexField()
sage: pari(2+i).arg()
0.463647609000806
The principal branch of 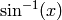 , so that
, so that
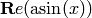 belongs to
belongs to ![[-\pi/2,\pi/2]](../../../_images/math/66273e69f0a4ec09632e01ece656e434bf620bb6.png) . If
. If
 is real and
is real and 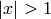 then
then 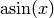 is complex.
is complex.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(pari(0.5).sin()).asin()
0.500000000000000
sage: pari(2).asin()
1.57079632679490 + 1.31695789692482*I
The principal branch of 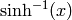 , so that
, so that
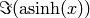 belongs to
belongs to ![[-\pi/2,\pi/2]](../../../_images/math/66273e69f0a4ec09632e01ece656e434bf620bb6.png) .
.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(2).asinh()
1.44363547517881
sage: C.<i> = ComplexField()
sage: pari(2+i).asinh()
1.52857091948100 + 0.427078586392476*I
The principal branch of 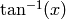 , so that
, so that
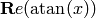 belongs to
belongs to ![]-\pi/2, \pi/2[](../../../_images/math/b877d5eb7afef5b1f7af8417c220e11624a7e203.png) .
.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(1).atan()
0.785398163397448
sage: C.<i> = ComplexField()
sage: pari(1.5+i).atan()
1.10714871779409 + 0.255412811882995*I
The principal branch of 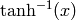 , so that
, so that
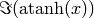 belongs to
belongs to ![]-\pi/2,\pi/2]](../../../_images/math/5708b45900c17f010ad04bd2af35528e7232566f.png) . If
. If
 is real and
is real and 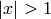 then
then 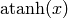 is complex.
is complex.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(0).atanh()
0.E-19
sage: pari(2).atanh()
0.549306144334055 + 1.57079632679490*I
The Bernoulli number  , where
, where  ,
,
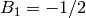 ,
, 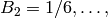 expressed as a
rational number. The argument
expressed as a
rational number. The argument  should be of type
integer.
should be of type
integer.
EXAMPLES:
sage: pari(18).bernfrac()
43867/798
sage: [pari(n).bernfrac() for n in range(10)]
[1, -1/2, 1/6, 0, -1/30, 0, 1/42, 0, -1/30, 0]
The Bernoulli number 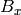 , as for the function bernfrac,
but
, as for the function bernfrac,
but 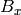 is returned as a real number (with the current
precision).
is returned as a real number (with the current
precision).
EXAMPLES:
sage: pari(18).bernreal()
54.9711779448622
Creates a vector containing, as rational numbers, the Bernoulli
numbers 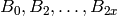 . This routine is
obsolete. Use bernfrac instead each time you need a Bernoulli
number in exact form.
. This routine is
obsolete. Use bernfrac instead each time you need a Bernoulli
number in exact form.
Note: this routine is implemented using repeated independent calls to bernfrac, which is faster than the standard recursion in exact arithmetic.
EXAMPLES:
sage: pari(8).bernvec()
[1, 1/6, -1/30, 1/42, -1/30, 5/66, -691/2730, 7/6, -3617/510]
sage: [pari(2*n).bernfrac() for n in range(9)]
[1, 1/6, -1/30, 1/42, -1/30, 5/66, -691/2730, 7/6, -3617/510]
The 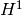 -Bessel function of index
-Bessel function of index 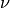 and
argument
and
argument  .
.
If 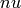 or
or  is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
EXAMPLES:
sage: pari(2).besselh1(3)
0.486091260585891 - 0.160400393484924*I
The 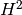 -Bessel function of index
-Bessel function of index 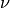 and
argument
and
argument  .
.
If 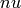 or
or  is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
EXAMPLES:
sage: pari(2).besselh2(3)
0.486091260585891 + 0.160400393484924*I
Bessel I function (Bessel function of the second kind), with index
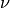 and argument
and argument  . If
. If  converts to
a power series, the initial factor
converts to
a power series, the initial factor
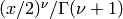 is omitted (since it cannot be
represented in PARI when
is omitted (since it cannot be
represented in PARI when 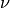 is not integral).
is not integral).
If 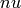 or
or  is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
EXAMPLES:
sage: pari(2).besseli(3)
2.24521244092995
sage: C.<i> = ComplexField()
sage: pari(2).besseli(3+i)
1.12539407613913 + 2.08313822670661*I
Bessel J function (Bessel function of the first kind), with index
 and argument
and argument  . If
. If  converts to
a power series, the initial factor
converts to
a power series, the initial factor
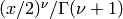 is omitted (since it cannot be
represented in PARI when
is omitted (since it cannot be
represented in PARI when 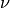 is not integral).
is not integral).
If 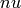 or
or  is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
EXAMPLES:
sage: pari(2).besselj(3)
0.486091260585891
J-Bessel function of half integral index (Spherical Bessel
function of the first kind). More precisely, besseljh(n,x) computes
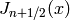 where n must an integer, and x is any
complex value. In the current implementation (PARI, version
2.2.11), this function is not very accurate when
where n must an integer, and x is any
complex value. In the current implementation (PARI, version
2.2.11), this function is not very accurate when  is
small.
is
small.
If 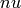 or
or  is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
EXAMPLES:
sage: pari(2).besseljh(3)
0.4127100324 # 32-bit
0.412710032209716 # 64-bit
nu.besselk(x, flag=0): K-Bessel function (modified Bessel function of the second kind) of index nu, which can be complex, and argument x.
If 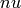 or
or  is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
INPUT:
EXAMPLES:
sage: C.<i> = ComplexField()
sage: pari(2+i).besselk(3)
0.0455907718407551 + 0.0289192946582081*I
sage: pari(2+i).besselk(-3)
-4.34870874986752 - 5.38744882697109*I
sage: pari(2+i).besselk(300, flag=1)
3.74224603319728 E-132 + 2.49071062641525 E-134*I
nu.besseln(x): Bessel N function (Spherical Bessel function of the second kind) of index nu and argument x.
If 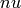 or
or  is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
EXAMPLES:
sage: C.<i> = ComplexField()
sage: pari(2+i).besseln(3)
-0.280775566958244 - 0.486708533223726*I
binary(x): gives the vector formed by the binary digits of abs(x), where x is of type t_INT.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(0).binary()
[0]
sage: pari(-5).binary()
[1, 0, 1]
sage: pari(5).binary()
[1, 0, 1]
sage: pari(2005).binary()
[1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1]
sage: pari('"2"').binary()
...
TypeError: x (=2) must be of type t_INT, but is of type t_STR.
binomial(x, k): return the binomial coefficient “x choose k”.
INPUT:
EXAMPLES:
sage: pari(6).binomial(2)
15
sage: pari('x+1').binomial(3)
1/6*x^3 - 1/6*x
sage: pari('2+x+O(x^2)').binomial(3)
1/3*x + O(x^2)
bitand(x,y): Bitwise and of two integers x and y. Negative numbers behave as if modulo some large power of 2.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(8).bitand(4)
0
sage: pari(8).bitand(8)
8
sage: pari(6).binary()
[1, 1, 0]
sage: pari(7).binary()
[1, 1, 1]
sage: pari(6).bitand(7)
6
sage: pari(19).bitand(-1)
19
sage: pari(-1).bitand(-1)
-1
bitneg(x,n=-1): Bitwise negation of the integer x truncated to n bits. n=-1 (the default) represents an infinite sequence of the bit 1. Negative numbers behave as if modulo some large power of 2.
With n=-1, this function returns -n-1. With n = 0, it returns a
number a such that 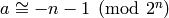 .
.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(10).bitneg()
-11
sage: pari(1).bitneg()
-2
sage: pari(-2).bitneg()
1
sage: pari(-1).bitneg()
0
sage: pari(569).bitneg()
-570
sage: pari(569).bitneg(10)
454
sage: 454 % 2^10
454
sage: -570 % 2^10
454
bitnegimply(x,y): Bitwise negated imply of two integers x and y, in other words, x BITAND BITNEG(y). Negative numbers behave as if modulo big power of 2.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(14).bitnegimply(0)
14
sage: pari(8).bitnegimply(8)
0
sage: pari(8+4).bitnegimply(8)
4
bitor(x,y): Bitwise or of two integers x and y. Negative numbers behave as if modulo big power of 2.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(14).bitor(0)
14
sage: pari(8).bitor(4)
12
sage: pari(12).bitor(1)
13
sage: pari(13).bitor(1)
13
bittest(x, long n): Returns bit number n (coefficient of
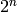 in binary) of the integer x. Negative numbers behave
as if modulo a big power of 2.
in binary) of the integer x. Negative numbers behave
as if modulo a big power of 2.
INPUT:
OUTPUT:
EXAMPLES:
sage: x = pari(6)
sage: x.bittest(0)
False
sage: x.bittest(1)
True
sage: x.bittest(2)
True
sage: x.bittest(3)
False
sage: pari(-3).bittest(0)
True
sage: pari(-3).bittest(1)
False
sage: [pari(-3).bittest(n) for n in range(10)]
[True, False, True, True, True, True, True, True, True, True]
bitxor(x,y): Bitwise exclusive or of two integers x and y. Negative numbers behave as if modulo big power of 2.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(6).bitxor(4)
2
sage: pari(0).bitxor(4)
4
sage: pari(6).bitxor(0)
6
bnf being as output by bnfinit, checks whether the result is correct, i.e. whether the calculation of the contents of self are correct without assuming the Generalized Riemann Hypothesis. If it is correct, the answer is 1. If not, the program may output some error message, but more probably will loop indefinitely. In no occasion can the program give a wrong answer (barring bugs of course): if the program answers 1, the answer is certified.
Warning
By default, most of the bnf routines depend on the
correctness of a heuristic assumption which is stronger
than GRH. In order to obtain a provably-correct result you
must specify 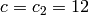 for the technical optional
parameters to the function. There are known counterexamples
for smaller
for the technical optional
parameters to the function. There are known counterexamples
for smaller  (which is the default).
(which is the default).
For real x: return the smallest integer = x. For rational functions: the quotient of numerator by denominator. For lists: apply componentwise.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(1.4).ceil()
2
sage: pari(-1.4).ceil()
-1
sage: pari(3/4).ceil()
1
sage: pari(x).ceil()
x
sage: pari((x^2+x+1)/x).ceil()
x + 1
This may be unexpected: but it is correct, treating the argument as a rational function in RR(x).
sage: pari(x^2+5*x+2.5).ceil()
x^2 + 5*x + 2.50000000000000
centerlift(x,v): Centered lift of x. This function returns exactly the same thing as lift, except if x is an integer mod.
INPUT:
OUTPUT: gen
EXAMPLES:
sage: x = pari(-2).Mod(5)
sage: x.centerlift()
-2
sage: x.lift()
3
sage: f = pari('x-1').Mod('x^2 + 1')
sage: f.centerlift()
x - 1
sage: f.lift()
x - 1
sage: f = pari('x-y').Mod('x^2+1')
sage: f
Mod(x - y, x^2 + 1)
sage: f.centerlift('x')
x - y
sage: f.centerlift('y')
Mod(x - y, x^2 + 1)
changevar(gen x, y): change variables of x according to the vector y.
Warning
This doesn’t seem to work right at all in Sage (!). Use with caution. STRANGE
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari('x^3+1').changevar(pari(['y']))
y^3 + 1
component(x, long n): Return n’th component of the internal representation of x. This function is 1-based instead of 0-based.
Note
For vectors or matrices, it is simpler to use x[n-1]. For list objects such as is output by nfinit, it is easier to use member functions.
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari([0,1,2,3,4]).component(1)
0
sage: pari([0,1,2,3,4]).component(2)
1
sage: pari([0,1,2,3,4]).component(4)
3
sage: pari('x^3 + 2').component(1)
2
sage: pari('x^3 + 2').component(2)
0
sage: pari('x^3 + 2').component(4)
1
sage: pari('x').component(0)
...
PariError: (8)
conj(x): Return the algebraic conjugate of x.
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari('x+1').conj()
x + 1
sage: pari('x+I').conj()
x - I
sage: pari('1/(2*x+3*I)').conj()
1/(2*x - 3*I)
sage: pari([1,2,'2-I','Mod(x,x^2+1)', 'Mod(x,x^2-2)']).conj()
[1, 2, 2 + I, Mod(-x, x^2 + 1), Mod(-x, x^2 - 2)]
sage: pari('Mod(x,x^2-2)').conj()
Mod(-x, x^2 - 2)
sage: pari('Mod(x,x^3-3)').conj()
...
PariError: incorrect type (20)
conjvec(x): Returns the vector of all conjugates of the algebraic number x. An algebraic number is a polynomial over Q modulo an irreducible polynomial.
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari('Mod(1+x,x^2-2)').conjvec()
[-0.414213562373095, 2.41421356237310]~
sage: pari('Mod(x,x^3-3)').conjvec()
[1.44224957030741, -0.721124785153704 + 1.24902476648341*I, -0.721124785153704 - 1.24902476648341*I]~
The cosine function.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(1.5).cos()
0.0707372016677029
sage: C.<i> = ComplexField()
sage: pari(1+i).cos()
0.833730025131149 - 0.988897705762865*I
sage: pari('x+O(x^8)').cos()
1 - 1/2*x^2 + 1/24*x^4 - 1/720*x^6 + 1/40320*x^8 + O(x^9)
The hyperbolic cosine function.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(1.5).cosh()
2.35240961524325
sage: C.<i> = ComplexField()
sage: pari(1+i).cosh()
0.833730025131149 + 0.988897705762865*I
sage: pari('x+O(x^8)').cosh()
1 + 1/2*x^2 + 1/24*x^4 + 1/720*x^6 + O(x^8)
The cotangent of x.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(5).cotan()
-0.295812915532746
Computing the cotangent of 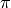 doesn’t raise an error,
but instead just returns a very large (positive or negative)
number.
doesn’t raise an error,
but instead just returns a very large (positive or negative)
number.
sage: x = RR(pi)
sage: pari(x).cotan() # random
-8.17674825 E15
denominator(x): Return the denominator of x. When x is a vector, this is the least common multiple of the denominators of the components of x.
what about poly? INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari('5/9').denominator()
9
sage: pari('(x+1)/(x-2)').denominator()
x - 2
sage: pari('2/3 + 5/8*x + 7/3*x^2 + 1/5*y').denominator()
1
sage: pari('2/3*x').denominator()
1
sage: pari('[2/3, 5/8, 7/3, 1/5]').denominator()
120
The principal branch of the dilogarithm of  , i.e. the
analytic continuation of the power series
, i.e. the
analytic continuation of the power series
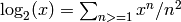 .
.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(1).dilog()
1.64493406684823
sage: C.<i> = ComplexField()
sage: pari(1+i).dilog()
0.616850275068085 + 1.46036211675312*I
e.disc(): return the discriminant of the elliptic curve e.
EXAMPLES:
sage: e = pari([0, -1, 1, -10, -20]).ellinit()
sage: e.disc()
-161051
sage: _.factor()
[-1, 1; 11, 5]
x.eint1(n): exponential integral E1(x):
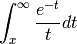
If n is present, output the vector [eint1(x), eint1(2*x), ..., eint1(n*x)]. This is faster than repeatedly calling eint1(i*x).
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
REFERENCE:
EXAMPLES:
e.elladd(z0, z1): return the sum of the points z0 and z1 on this elliptic curve.
INPUT:
OUTPUT: point on E
EXAMPLES: First we create an elliptic curve:
sage: e = pari([0, 1, 1, -2, 0]).ellinit()
sage: str(e)[:65] # first part of output
'[0, 1, 1, -2, 0, 4, -4, 1, -3, 112, -856, 389, 1404928/389, [0.90'
Next we add two points on the elliptic curve. Notice that the Python lists are automatically converted to PARI objects so you don’t have to do that explicitly in your code.
sage: e.elladd([1,0], [-1,1])
[-3/4, -15/8]
e.ellak(n): Returns the coefficient 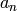 of the
of the
 -function of the elliptic curve e, i.e. the
-function of the elliptic curve e, i.e. the
 -th Fourier coefficient of the weight 2 newform
associated to e (according to Shimura-Taniyama).
-th Fourier coefficient of the weight 2 newform
associated to e (according to Shimura-Taniyama).
The curvemust be a medium or long vector of the type given by ellinit. For this function to work for every n and not just those prime to the conductor, e must be a minimal Weierstrass equation. If this is not the case, use the function ellminimalmodel first before using ellak (or you will get INCORRECT RESULTS!)
INPUT:
EXAMPLES:
sage: e = pari([0, -1, 1, -10, -20]).ellinit()
sage: e.ellak(6)
2
sage: e.ellak(2005)
2
sage: e.ellak(-1)
0
sage: e.ellak(0)
0
Return the first  Fourier coefficients of the modular
form attached to this elliptic curve. See ellak for more details.
Fourier coefficients of the modular
form attached to this elliptic curve. See ellak for more details.
INPUT:
EXAMPLES:
sage: e = pari([0, -1, 1, -10, -20]).ellinit()
sage: e.ellan(3)
[1, -2, -1]
sage: e.ellan(20)
[1, -2, -1, 2, 1, 2, -2, 0, -2, -2, 1, -2, 4, 4, -1, -4, -2, 4, 0, 2]
sage: e.ellan(-1)
[]
sage: v = e.ellan(10, python_ints=True); v
[1, -2, -1, 2, 1, 2, -2, 0, -2, -2]
sage: type(v)
<type 'list'>
sage: type(v[0])
<type 'int'>
e.ellap(p): Returns the prime-indexed coefficient 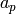 of
the
of
the  -function of the elliptic curve
-function of the elliptic curve  , i.e.
the
, i.e.
the  -th Fourier coefficient of the newform attached to
e.
-th Fourier coefficient of the newform attached to
e.
The computation uses the baby-step giant-step method and a trick
due to Mestre, and requires 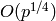 time and
time and
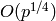 storage.
storage.
If p is not prime, this function will return an incorrect answer.
The curve e must be a medium or long vector of the type given by ellinit. For this function to work for every n and not just those prime to the conductor, e must be a minimal Weierstrass equation. If this is not the case, use the function ellminimalmodel first before using ellap (or you will get INCORRECT RESULTS!)
INPUT:
EXAMPLES:
sage: e = pari([0, -1, 1, -10, -20]).ellinit()
sage: e.ellap(2)
-2
sage: e.ellap(2003)
4
sage: e.ellak(-1)
0
e.ellaplist(n): Returns a PARI list of all the prime-indexed
coefficients 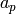 (up to n) of the
(up to n) of the  -function
of the elliptic curve
-function
of the elliptic curve  , i.e. the Fourier coefficients of
the newform attached to
, i.e. the Fourier coefficients of
the newform attached to  .
.
INPUT:
n - a long integer
python_ints - bool (default is False); if True, return a list of Python ints instead of a PARI gen wrapper.
The curve e must be a medium or long vector of the type given by ellinit. For this function to work for every n and not just those prime to the conductor, e must be a minimal Weierstrass equation. If this is not the case, use the function ellminimalmodel first before using ellaplist (or you will get INCORRECT RESULTS!)
INPUT:
EXAMPLES:
sage: e = pari([0, -1, 1, -10, -20]).ellinit()
sage: v = e.ellaplist(10); v
[-2, -1, 1, -2]
sage: type(v)
<type 'sage.libs.pari.gen.gen'>
sage: v.type()
't_VEC'
sage: e.ellan(10)
[1, -2, -1, 2, 1, 2, -2, 0, -2, -2]
sage: v = e.ellaplist(10, python_ints=True); v
[-2, -1, 1, -2]
sage: type(v)
<type 'list'>
sage: type(v[0])
<type 'int'>
e.ellbil(z0, z1): return the value of the canonical bilinear form on z0 and z1.
INPUT:
EXAMPLES:
sage: e = pari([0,1,1,-2,0]).ellinit().ellminimalmodel()[0]
sage: e.ellbil([1, 0], [-1, 1])
0.418188984498861
e.ellchangecurve(ch): return the new model (equation) for the elliptic curve e given by the change of coordinates ch.
The change of coordinates is specified by a vector ch=[u,r,s,t]; if
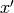 and
and 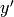 are the new coordinates, then
are the new coordinates, then
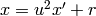 and
and 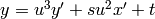 .
.
INPUT:
EXAMPLES:
sage: e = pari([1,2,3,4,5]).ellinit()
sage: e.ellglobalred()
[10351, [1, -1, 0, -1], 1]
sage: f = e.ellchangecurve([1,-1,0,-1])
sage: f[:5]
[1, -1, 0, 4, 3]
self.ellchangepoint(y): change data on point or vector of points self on an elliptic curve according to y=[u,r,s,t]
EXAMPLES:
sage: e = pari([0,1,1,-2,0]).ellinit()
sage: x = pari([1,0])
sage: e.ellisoncurve([1,4])
False
sage: e.ellisoncurve(x)
True
sage: f = e.ellchangecurve([1,2,3,-1])
sage: f[:5] # show only first five entries
[6, -2, -1, 17, 8]
sage: x.ellchangepoint([1,2,3,-1])
[-1, 4]
sage: f.ellisoncurve([-1,4])
True
om.elleisnum(k, flag=0): om=[om1,om2] being a 2-component vector giving a basis of a lattice L and k an even positive integer, computes the numerical value of the Eisenstein series of weight k. When flag is non-zero and k=4 or 6, this gives g2 or g3 with the correct normalization.
INPUT:
OUTPUT:
EXAMPLES:
sage: e = pari([0,1,1,-2,0]).ellinit()
sage: om = e.omega()
sage: om
[2.49021256085506, 1.97173770155165*I]
sage: om.elleisnum(2)
-5.28864933965426
sage: om.elleisnum(4)
112.000000000000
sage: om.elleisnum(100)
2.15314248576078 E50
e.elleta(): return the vector [eta1,eta2] of quasi-periods associated with the period lattice e.omega() of the elliptic curve e.
EXAMPLES:
sage: e = pari([0,0,0,-82,0]).ellinit()
sage: e.elleta()
[3.60546360143265, 10.8163908042980*I]
e.ellglobalred(): return information related to the global minimal model of the elliptic curve e.
INPUT:
OUTPUT:
EXAMPLES:
sage: e = pari([0, 5, 2, -1, 1]).ellinit()
sage: e.ellglobalred()
[20144, [1, -2, 0, -1], 1]
sage: e = pari(EllipticCurve('17a').a_invariants()).ellinit()
sage: e.ellglobalred()
[17, [1, 0, 0, 0], 4]
e.ellheight(a, flag=2): return the global Neron-Tate height of the point a on the elliptic curve e.
INPUT:
e - elliptic curve over  ,
assumed to be in a standard minimal integral model (as given by
ellminimalmodel)
,
assumed to be in a standard minimal integral model (as given by
ellminimalmodel)
a - rational point on e
flag (optional) - specifies which algorithm to be used for computing the archimedean local height:
due to J. Silverman
1 - uses Tate’s 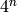 algorithm
algorithm
2 - uses Mestre’s AGM algorithm (this is the default, being faster than the other two)
precision (optional) - the precision of the result, in bits.
Note that in order to achieve the desired precision, the elliptic curve must have been created using ellinit with the desired precision.
EXAMPLES:
sage: e = pari([0,1,1,-2,0]).ellinit().ellminimalmodel()[0]
sage: e.ellheight([1,0])
0.476711659343740
sage: e.ellheight([1,0], flag=0)
0.476711659343740
sage: e.ellheight([1,0], flag=1)
0.476711659343740
e.ellheightmatrix(x): return the height matrix for the vector x of points on the elliptic curve e.
In other words, it returns the Gram matrix of x with respect to the height bilinear form on e (see ellbil).
INPUT:
 ,
assumed to be in a standard minimal integral model (as given by
ellminimalmodel)
,
assumed to be in a standard minimal integral model (as given by
ellminimalmodel)EXAMPLES:
sage: e = pari([0,1,1,-2,0]).ellinit().ellminimalmodel()[0]
sage: e.ellheightmatrix([[1,0], [-1,1]])
[0.476711659343740, 0.418188984498861; 0.418188984498861, 0.686667083305587]
Return the Pari elliptic curve object with Weierstrass coefficients given by self, a list with 5 elements.
INPUT:
self - a list of 5 coefficients
flag (optional, default: 0) - if 0, ask for a Pari ell structure with 19 components; if 1, ask for a Pari sell structure with only the first 13 components
precision (optional, default: 0) - the real precision to be used in the computation of the components of the Pari (s)ell structure; if 0, use the default 53 bits.
Note
the parameter precision in ellinit() controls not only the real precision of the resulting (s)ell structure, but also the precision of most subsequent computations with this elliptic curve. You should therefore set it from the start to the value you require.
OUTPUT:
EXAMPLES: An elliptic curve with integer coefficients:
sage: e = pari([0,1,0,1,0]).ellinit(); e
[0, 1, 0, 1, 0, 4, 2, 0, -1, -32, 224, -48, 2048/3, [0.E-28, -0.500000000000000 - 0.866025403784439*I, -0.500000000000000 + 0.866025403784439*I]~, 3.37150070962519, 1.68575035481260 + 2.15651564749964*I, -0.687257278928726 + 7.57138254 E-30*I, -0.343628639464363 - 1.37139930484298*I, 7.27069403586288] # 32-bit
[0, 1, 0, 1, 0, 4, 2, 0, -1, -32, 224, -48, 2048/3, [0.E-38, -0.500000000000000 - 0.866025403784439*I, -0.500000000000000 + 0.866025403784439*I]~, 3.37150070962519, 1.68575035481260 + 2.15651564749964*I, -0.687257278928726 + 1.76284987179941 E-39*I, -0.343628639464363 - 1.37139930484298*I, 7.27069403586288] # 64-bit
Its inexact components have the default precision of 53 bits:
sage: RR(e[14])
3.37150070962519
We can compute this to higher precision:
sage: R = RealField(150)
sage: e = pari([0,1,0,1,0]).ellinit(precision=150)
sage: R(e[14])
3.3715007096251920857424073155981539790016018
Using flag=1 returns a short elliptic curve Pari object:
sage: pari([0,1,0,1,0]).ellinit(flag=1)
[0, 1, 0, 1, 0, 4, 2, 0, -1, -32, 224, -48, 2048/3]
The coefficients can be any ring elements that convert to Pari:
sage: pari([0,1/2,0,-3/4,0]).ellinit(flag=1)
[0, 1/2, 0, -3/4, 0, 2, -3/2, 0, -9/16, 40, -116, 117/4, 256000/117]
sage: pari([0,0.5,0,-0.75,0]).ellinit(flag=1)
[0, 0.500000000000000, 0, -0.750000000000000, 0, 2.00000000000000, -1.50000000000000, 0, -0.562500000000000, 40.0000000000000, -116.000000000000, 29.2500000000000, 2188.03418803419]
sage: pari([0,I,0,1,0]).ellinit(flag=1)
[0, I, 0, 1, 0, 4*I, 2, 0, -1, -64, 352*I, -80, 16384/5]
sage: pari([0,x,0,2*x,1]).ellinit(flag=1)
[0, x, 0, 2*x, 1, 4*x, 4*x, 4, -4*x^2 + 4*x, 16*x^2 - 96*x, -64*x^3 + 576*x^2 - 864, 64*x^4 - 576*x^3 + 576*x^2 - 432, (256*x^6 - 4608*x^5 + 27648*x^4 - 55296*x^3)/(4*x^4 - 36*x^3 + 36*x^2 - 27)]
e.ellisoncurve(x): return True if the point x is on the elliptic curve e, False otherwise.
If the point or the curve have inexact coefficients, an attempt is made to take this into account.
EXAMPLES:
sage: e = pari([0,1,1,-2,0]).ellinit()
sage: e.ellisoncurve([1,0])
True
sage: e.ellisoncurve([1,1])
False
sage: e.ellisoncurve([1,0.00000000000000001])
False
sage: e.ellisoncurve([1,0.000000000000000001])
True
sage: e.ellisoncurve([0])
True
e.elllocalred(p): computes the data of local reduction at the prime p on the elliptic curve e
For more details on local reduction and Kodaira types, see IV.8 and IV.9 in J. Silverman’s book “Advanced topics in the arithmetic of elliptic curves”.
INPUT:

OUTPUT:
 : good reduction,
nonsingular curve of genus 1
: good reduction,
nonsingular curve of genus 1 : rational curve with a
cusp
: rational curve with a
cusp : two nonsingular rational
curves intersecting tangentially at one point
: two nonsingular rational
curves intersecting tangentially at one point : three nonsingular
rational curves intersecting at one point
: three nonsingular
rational curves intersecting at one point : rational curve with a
node
: rational curve with a
node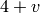 , then
it is type
, then
it is type 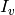 :
:  nonsingular rational curves
arranged as a
nonsingular rational curves
arranged as a  -gon
-gon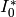 : nonsingular rational
curve of multiplicity two with four nonsingular rational curves of
multiplicity one attached
: nonsingular rational
curve of multiplicity two with four nonsingular rational curves of
multiplicity one attached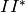 : nine nonsingular
rational curves in a special configuration
: nine nonsingular
rational curves in a special configuration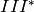 : eight nonsingular
rational curves in a special configuration
: eight nonsingular
rational curves in a special configuration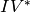 : seven nonsingular
rational curves in a special configuration
: seven nonsingular
rational curves in a special configuration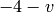 ,
then it is type
,
then it is type 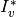 : chain of
: chain of 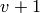 nonsingular rational curves of multiplicity two, with two
nonsingular rational curves of multiplicity one attached at either
end
nonsingular rational curves of multiplicity two, with two
nonsingular rational curves of multiplicity one attached at either
end
EXAMPLES:
Type  :
:
sage: e = pari([0,0,0,0,1]).ellinit()
sage: e.elllocalred(7)
[0, 1, [1, 0, 0, 0], 1]
Type  :
:
sage: e = pari(EllipticCurve('27a3').a_invariants()).ellinit()
sage: e.elllocalred(3)
[3, 2, [1, -1, 0, 1], 1]
Type 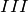 :
:
sage: e = pari(EllipticCurve('24a4').a_invariants()).ellinit()
sage: e.elllocalred(2)
[3, 3, [1, 1, 0, 1], 2]
Type 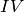 :
:
sage: e = pari(EllipticCurve('20a2').a_invariants()).ellinit()
sage: e.elllocalred(2)
[2, 4, [1, 1, 0, 1], 3]
Type 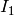 :
:
sage: e = pari(EllipticCurve('11a2').a_invariants()).ellinit()
sage: e.elllocalred(11)
[1, 5, [1, 0, 0, 0], 1]
Type 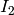 :
:
sage: e = pari(EllipticCurve('14a4').a_invariants()).ellinit()
sage: e.elllocalred(2)
[1, 6, [1, 0, 0, 0], 2]
Type 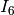 :
:
sage: e = pari(EllipticCurve('14a1').a_invariants()).ellinit()
sage: e.elllocalred(2)
[1, 10, [1, 0, 0, 0], 2]
Type 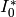 :
:
sage: e = pari(EllipticCurve('32a3').a_invariants()).ellinit()
sage: e.elllocalred(2)
[5, -1, [1, 1, 1, 0], 1]
Type 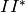 :
:
sage: e = pari(EllipticCurve('24a5').a_invariants()).ellinit()
sage: e.elllocalred(2)
[3, -2, [1, 2, 1, 4], 1]
Type 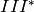 :
:
sage: e = pari(EllipticCurve('24a2').a_invariants()).ellinit()
sage: e.elllocalred(2)
[3, -3, [1, 2, 1, 4], 2]
Type 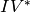 :
:
sage: e = pari(EllipticCurve('20a1').a_invariants()).ellinit()
sage: e.elllocalred(2)
[2, -4, [1, 0, 1, 2], 3]
Type 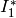 :
:
sage: e = pari(EllipticCurve('24a1').a_invariants()).ellinit()
sage: e.elllocalred(2)
[3, -5, [1, 0, 1, 2], 4]
Type 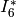 :
:
sage: e = pari(EllipticCurve('90c2').a_invariants()).ellinit()
sage: e.elllocalred(3)
[2, -10, [1, 96, 1, 316], 4]
e.elllseries(s, A=1): return the value of the  -series of
the elliptic curve e at the complex number s.
-series of
the elliptic curve e at the complex number s.
This uses an 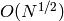 algorithm in the conductor N of
e, so it is impractical for large conductors (say greater than
algorithm in the conductor N of
e, so it is impractical for large conductors (say greater than
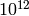 ).
).
INPUT:

EXAMPLES:
sage: e = pari([0,1,1,-2,0]).ellinit()
sage: e.elllseries(2.1)
0.402838047956645
sage: e.elllseries(1) # random, close to 0
1.822829333527862 E-19
sage: e.elllseries(-2)
0
The following example differs for the last digit on 32 vs. 64 bit systems
sage: e.elllseries(2.1, A=1.1)
0.402838047956645
ellminimalmodel(e): return the standard minimal integral model of the rational elliptic curve e and the corresponding change of variables. INPUT:
OUTPUT:
EXAMPLES:
sage: e = pari([1,2,3,4,5]).ellinit()
sage: F, ch = e.ellminimalmodel()
sage: F[:5]
[1, -1, 0, 4, 3]
sage: ch
[1, -1, 0, -1]
sage: e.ellchangecurve(ch)[:5]
[1, -1, 0, 4, 3]
e.ellorder(x): return the order of the point x on the elliptic curve e (return 0 if x is not a torsion point)
INPUT:

EXAMPLES:
sage: e = pari(EllipticCurve('65a1').a_invariants()).ellinit()
A point of order two:
sage: e.ellorder([0,0])
2
And a point of infinite order:
sage: e.ellorder([1,0])
0
e.ellordinate(x): return the  -coordinates of the points
on the elliptic curve e having x as
-coordinates of the points
on the elliptic curve e having x as  -coordinate.
-coordinate.
INPUT:
EXAMPLES:
sage: e = pari([0,1,1,-2,0]).ellinit()
sage: e.ellordinate(0)
[0, -1]
sage: C.<i> = ComplexField()
sage: e.ellordinate(i)
[0.582203589721741 - 1.38606082464177*I, -1.58220358972174 + 1.38606082464177*I]
sage: e.ellordinate(1+3*5^1+O(5^3))
[4*5 + 5^2 + O(5^3), 4 + 3*5^2 + O(5^3)]
sage: e.ellordinate('z+2*z^2+O(z^4)')
[-2*z - 7*z^2 - 23*z^3 + O(z^4), -1 + 2*z + 7*z^2 + 23*z^3 + O(z^4)]
e.ellpointtoz(P): return the complex number (in the fundamental parallelogram) corresponding to the point P on the elliptic curve e, under the complex uniformization of e given by the Weierstrass p-function.
The complex number z returned by this function lies in the parallelogram formed by the real and complex periods of e, as given by e.omega().
EXAMPLES:
sage: e = pari([0,0,0,1,0]).ellinit()
sage: e.ellpointtoz([0,0])
1.85407467730137
The point at infinity is sent to the complex number 0:
sage: e.ellpointtoz([0])
0
e.ellpow(z, n): return n times the point z on the elliptic curve e.
INPUT:
EXAMPLES: We consider a CM curve:
sage: e = pari([0,0,0,1,0]).ellinit()
Multiplication by two:
sage: e.ellpow([0,0], 2)
[0]
Complex multiplication (this is broken at the moment):
sage: e.ellpow([0,0], I+1) # optional
e.ellrootno(p): return the (local or global) root number of the
 -series of the elliptic curve e
-series of the elliptic curve e
If p is a prime number, the local root number at p is returned. If
p is 1, the global root number is returned. Note that the global
root number is the sign of the functional equation of the
 -series, and therefore conjecturally equal to the parity
of the rank of e.
-series, and therefore conjecturally equal to the parity
of the rank of e.
INPUT:

OUTPUT: 1 or -1
EXAMPLES: Here is a curve of rank 3:
sage: e = pari([0,0,0,-82,0]).ellinit()
sage: e.ellrootno()
-1
sage: e.ellrootno(2)
1
sage: e.ellrootno(1009)
1
e.ellsigma(z, flag=0): return the value at the complex point z of
the Weierstrass 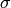 function associated to the
elliptic curve e.
function associated to the
elliptic curve e.
EXAMPLES:
sage: e = pari([0,0,0,1,0]).ellinit()
sage: C.<i> = ComplexField()
sage: e.ellsigma(2+i)
1.43490215804166 + 1.80307856719256*I
e.ellsub(z0, z1): return z0-z1 on this elliptic curve.
INPUT:
OUTPUT: point on E
EXAMPLES:
sage: e = pari([0, 1, 1, -2, 0]).ellinit()
sage: e.ellsub([1,0], [-1,1])
[0, 0]
e.elltors(flag = 0): return information about the torsion subgroup of the elliptic curve e
INPUT:

OUTPUT:
EXAMPLES:
sage: e = pari([1,0,1,-19,26]).ellinit()
sage: e.elltors()
[12, [6, 2], [[-2, 8], [3, -2]]]
ellwp(E, z,flag=0): Return the complex value of the Weierstrass P-function at z on the lattice defined by e.
INPUT:
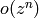 .
.OUTPUT:
EXAMPLES:
We first define the elliptic curve X_0(11):
sage: E = pari([0,-1,1,-10,-20]).ellinit()
Compute P(1).
sage: E.ellwp(1)
13.9658695257485 + 0.E-18*I
Compute P(1+i), where i = sqrt(-1).
sage: C.<i> = ComplexField()
sage: E.ellwp(pari(1+i))
-1.11510682565555 + 2.33419052307470*I
sage: E.ellwp(1+i)
-1.11510682565555 + 2.33419052307470*I
The series expansion, to the default 20 precision:
sage: E.ellwp()
z^-2 + 31/15*z^2 + 2501/756*z^4 + 961/675*z^6 + 77531/41580*z^8 + 1202285717/928746000*z^10 + 2403461/2806650*z^12 + 30211462703/43418875500*z^14 + 3539374016033/7723451736000*z^16 + 413306031683977/1289540602350000*z^18 + O(z^20)
Compute the series for wp to lower precision:
sage: E.ellwp(n=4)
z^-2 + 31/15*z^2 + O(z^4)
Next we use the version where the input is generators for a lattice:
sage: pari([1.2692, 0.63 + 1.45*i]).ellwp(1)
13.9656146936689 + 0.000644829272810...*I
With flag 1 compute the pair P(z) and P’(z):
sage: E.ellwp(1, flag=1)
[13.9658695257485 + 0.E-18*I, 50.5619300880073 ... E-18*I]
With flag=2, the computed pair is (x,y) on the curve instead of [P(z),P’(z)]:
sage: E.ellwp(1, flag=2)
[14.2992028590818 + 0.E-18*I, 50.0619300880073 ... E-18*I]
e.ellzeta(z): return the value at the complex point z of the
Weierstrass 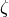 function associated with the elliptic
curve e.
function associated with the elliptic
curve e.
Note
This function has infinitely many poles (one of which is at z=0); attempting to evaluate it too close to one of the poles will result in a PariError.
INPUT:
EXAMPLES:
sage: e = pari([0,0,0,1,0]).ellinit()
sage: e.ellzeta(1)
1.06479841295883 + 0.E-19*I # 32-bit
1.06479841295883 - 5.42101086242752 E-20*I # 64-bit
sage: C.<i> = ComplexField()
sage: e.ellzeta(i-1)
-0.350122658523049 - 0.350122658523049*I
e.ellztopoint(z): return the point on the elliptic curve e corresponding to the complex number z, under the usual complex uniformization of e by the Weierstrass p-function.
INPUT:
OUTPUT point on e
EXAMPLES:
sage: e = pari([0,0,0,1,0]).ellinit()
sage: C.<i> = ComplexField()
sage: e.ellztopoint(1+i)
[0.E-19 - 1.02152286795670*I, -0.149072813701096 - 0.149072813701096*I] # 32-bit
[8.67655312026478 E-20 - 1.02152286795670*I, -0.149072813701096 - 0.149072813701096*I] # 64-bit
Complex numbers belonging to the period lattice of e are of course sent to the point at infinity on e:
sage: e.ellztopoint(0)
[0]
Return the complementary error function:
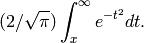
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(1).erfc()
0.157299207050285
x.eta(flag=0): if flag=0, 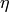 function without the
function without the
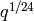 ; otherwise
; otherwise 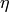 of the complex number
of the complex number
 in the upper half plane intelligently computed using
in the upper half plane intelligently computed using
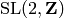 transformations.
transformations.
DETAILS: This functions computes the following. If the input
 is a complex number with positive imaginary part, the
result is
is a complex number with positive imaginary part, the
result is 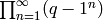 , where
, where
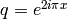 . If
. If  is a power series
(or can be converted to a power series) with positive valuation,
the result is
is a power series
(or can be converted to a power series) with positive valuation,
the result is 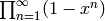 .
.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: C.<i> = ComplexField()
sage: pari(i).eta()
0.998129069925959 + 0.E-21*I
x.exp(): exponential of x.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(0).exp()
1.00000000000000
sage: pari(1).exp()
2.71828182845905
sage: pari('x+O(x^8)').exp()
1 + x + 1/2*x^2 + 1/6*x^3 + 1/24*x^4 + 1/120*x^5 + 1/720*x^6 + 1/5040*x^7 + O(x^8)
Return the factorization of x.
INPUT:
proof - (default: True) optional. If False (not the default),
returned factors  may only be pseudoprimes.
may only be pseudoprimes.
Note
In the standard PARI/GP interpreter and C-library the factor command always has proof=False, so beware!
EXAMPLES:
sage: pari('x^10-1').factor()
[x - 1, 1; x + 1, 1; x^4 - x^3 + x^2 - x + 1, 1; x^4 + x^3 + x^2 + x + 1, 1]
sage: pari(2^100-1).factor()
[3, 1; 5, 3; 11, 1; 31, 1; 41, 1; 101, 1; 251, 1; 601, 1; 1801, 1; 4051, 1; 8101, 1; 268501, 1]
sage: pari(2^100-1).factor(proof=False)
[3, 1; 5, 3; 11, 1; 31, 1; 41, 1; 101, 1; 251, 1; 601, 1; 1801, 1; 4051, 1; 8101, 1; 268501, 1]
We illustrate setting a limit:
sage: pari(next_prime(10^50)*next_prime(10^60)*next_prime(10^4)).factor(10^5)
[10007, 1; 100000000000000000000000000000000000000000000000151000000000700000000000000000000000000000000000000000000001057, 1]
PARI doesn’t have an algorithm for factoring multivariate polynomials:
sage: pari('x^3 - y^3').factor()
...
PariError: sorry, (15)
Return the Fibonacci number of index x.
EXAMPLES:
sage: pari(18).fibonacci()
2584
sage: [pari(n).fibonacci() for n in range(10)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
For real x: return the largest integer = x. For rational functions: the quotient of numerator by denominator. For lists: apply componentwise.
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari(5/9).floor()
0
sage: pari(11/9).floor()
1
sage: pari(1.17).floor()
1
sage: pari([1.5,2.3,4.99]).floor()
[1, 2, 4]
sage: pari([[1.1,2.2],[3.3,4.4]]).floor()
[[1, 2], [3, 4]]
sage: pari(x).floor()
x
sage: pari((x^2+x+1)/x).floor()
x + 1
sage: pari(x^2+5*x+2.5).floor()
x^2 + 5*x + 2.50000000000000
sage: pari('"hello world"').floor()
...
PariError: incorrect type (20)
frac(x): Return the fractional part of x, which is x - floor(x).
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari(1.75).frac()
0.750000000000000
sage: pari(sqrt(2)).frac()
0.414213562373095
sage: pari('sqrt(-2)').frac()
...
PariError: incorrect type (20)
s.gamma(precision): Gamma function at s.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(2).gamma()
1.00000000000000
sage: pari(5).gamma()
24.0000000000000
sage: C.<i> = ComplexField()
sage: pari(1+i).gamma()
0.498015668118356 - 0.154949828301811*I
TESTS:
sage: pari(-1).gamma()
...
PariError: (8)
s.gammah(): Gamma function evaluated at the argument x+1/2.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(2).gammah()
1.32934038817914
sage: pari(5).gammah()
52.3427777845535
sage: C.<i> = ComplexField()
sage: pari(1+i).gammah()
0.575315188063452 + 0.0882106775440939*I
a.hyperu(b,x): U-confluent hypergeometric function.
If  ,
,  , or
, or  is an exact argument,
it is first converted to a real or complex number using the
optional parameter precision (in bits). If the arguments are
inexact (e.g. real), the smallest of their precisions is used in
the computation, and the parameter precision is ignored.
is an exact argument,
it is first converted to a real or complex number using the
optional parameter precision (in bits). If the arguments are
inexact (e.g. real), the smallest of their precisions is used in
the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(1).hyperu(2,3)
0.333333333333333
Given two integral ideals x and y of a pari number field self, return an element a of the field (expressed in the integral basis of self) such that a*x is an integral ideal coprime to y.
EXAMPLES:
sage: F = NumberField(x^3-2, 'alpha')
sage: nf = F._pari_()
sage: x = pari('[1, -1, 2]~')
sage: y = pari('[1, -1, 3]~')
sage: nf.idealcoprime(x, y)
[1, 0, 0]~
sage: y = pari('[2, -2, 4]~')
sage: nf.idealcoprime(x, y)
[5/43, 9/43, -1/43]~
Return the discrete logarithm of the unit x in (ring of integers)/bid.
INPUT:
OUTPUT:
EXAMPLE:
sage: F = NumberField(x^3-2, 'alpha')
sage: nf = F._pari_()
sage: I = pari('[1, -1, 2]~')
sage: bid = nf.idealstar(I)
sage: x = pari('5')
sage: nf.ideallog(x, bid)
[25]~
Return the big ideal (bid) structure of modulus I.
INPUT:
EXAMPLE:
sage: F = NumberField(x^3-2, 'alpha')
sage: nf = F._pari_()
sage: I = pari('[1, -1, 2]~')
sage: nf.idealstar(I)
[[[43, 9, 5; 0, 1, 0; 0, 0, 1], [0]], [42, [42]], Mat([[43, [9, 1, 0]~, 1, 1, [-5, -9, 1]~], 1]), [[[[42], [[3, 0, 0]~], [[3, 0, 0]~], [[]~], 1]], [[], [], [;]]], Mat(1)]
imag(x): Return the imaginary part of x. This function also works component-wise.
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari('1+2*I').imag()
2
sage: pari(sqrt(-2)).imag()
1.41421356237310
sage: pari('x+I').imag()
1
sage: pari('x+2*I').imag()
2
sage: pari('(1+I)*x^2+2*I').imag()
x^2 + 2
sage: pari('[1,2,3] + [4*I,5,6]').imag()
[4, 0, 0]
s.incgam(x, y, precision): incomplete gamma function. y is optional and is the precomputed value of gamma(s).
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: C.<i> = ComplexField()
sage: pari(1+i).incgam(3-i)
-0.0458297859919946 + 0.0433696818726677*I
s.incgamc(x): complementary incomplete gamma function.
The arguments  and
and  are complex numbers such
that
are complex numbers such
that  is not a pole of
is not a pole of  and
and
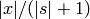 is not much larger than
is not much larger than  (otherwise, the convergence is very slow). The function returns the
value of the integral
(otherwise, the convergence is very slow). The function returns the
value of the integral
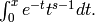
If  or
or  is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
EXAMPLES:
sage: pari(1).incgamc(2)
0.864664716763387
Returns int form of self, but raises an exception if int does not fit into a long integer.
This is about 5 times faster than the usual int conversion.
Returns Python int list form of entries of self, but raises an exception if int does not fit into a long integer. Here self must be a vector.
EXAMPLES:
sage: pari('[3,4,5]').type()
't_VEC'
sage: pari('[3,4,5]').intvec_unsafe()
[3, 4, 5]
sage: type(pari('[3,4,5]').intvec_unsafe()[0])
<type 'int'>
TESTS:
sage: pari(3).intvec_unsafe()
...
TypeError: gen must be of PARI type t_VEC
sage: pari('[2^150,1]').intvec_unsafe()
...
PariError: impossible assignment I-->S (23)
Determine whether or not self is a perfect k-th power. If k is not specified, find the largest k so that self is a k-th power.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(9).ispower()
(2, 3)
sage: pari(17).ispower()
(1, 17)
sage: pari(17).ispower(2)
(False, None)
sage: pari(17).ispower(1)
(1, 17)
sage: pari(2).ispower()
(1, 2)
isprime(x, flag=0): Returns True if x is a PROVEN prime number, and False otherwise.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(9).isprime()
False
sage: pari(17).isprime()
True
sage: n = pari(561) # smallest Carmichael number
sage: n.isprime() # not just a pseudo-primality test!
False
sage: n.isprime(1)
False
sage: n.isprime(2)
False
ispseudoprime(x, flag=0): Returns True if x is a pseudo-prime number, and False otherwise.
INPUT:
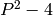 is not a square mod x). 0: checks whether x is a
strong Miller-Rabin pseudo prime for flag randomly chosen bases
(with end-matching to catch square roots of -1).
is not a square mod x). 0: checks whether x is a
strong Miller-Rabin pseudo prime for flag randomly chosen bases
(with end-matching to catch square roots of -1).OUTPUT:
EXAMPLES:
sage: pari(9).ispseudoprime()
False
sage: pari(17).ispseudoprime()
True
sage: n = pari(561) # smallest Carmichael number
sage: n.ispseudoprime() # not just any old pseudo-primality test!
False
sage: n.ispseudoprime(2)
False
EXAMPLES:
sage: pari(10).issquarefree()
True
sage: pari(20).issquarefree()
False
e.j(): return the j-invariant of the elliptic curve e.
EXAMPLES:
sage: e = pari([0, -1, 1, -10, -20]).ellinit()
sage: e.j()
-122023936/161051
sage: _.factor()
[-1, 1; 2, 12; 11, -5; 31, 3]
Return the least common multiple of x and y. EXAMPLES:
sage: pari(10).lcm(15)
30
lift(x,v): Returns the lift of an element of Z/nZ to Z or R[x]/(P) to R[x] for a type R if v is omitted. If v is given, lift only polymods with main variable v. If v does not occur in x, lift only intmods.
INPUT:
OUTPUT: gen
EXAMPLES:
sage: x = pari("x")
sage: a = x.Mod('x^3 + 17*x + 3')
sage: a
Mod(x, x^3 + 17*x + 3)
sage: b = a^4; b
Mod(-17*x^2 - 3*x, x^3 + 17*x + 3)
sage: b.lift()
-17*x^2 - 3*x
??? more examples
This method is deprecated, please use log_gamma() instead.
See the log_gamma() method for documentation and examples.
EXAMPLES:
sage: pari(100).lngamma()
doctest:...: DeprecationWarning: The method lngamma() is deprecated. Use log_gamma() instead.
359.134205369575
x.log(): natural logarithm of x.
This function returns the principal branch of the natural logarithm
of  , i.e., the branch such that
, i.e., the branch such that
![\Im(\log(x)) \in ]-\pi, \pi].](../../../_images/math/43a85b3493d9a066b42509dc2f82ec9e5cb61286.png) The result is
complex (with imaginary part equal to
The result is
complex (with imaginary part equal to 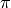 ) if
) if
 and
and  . In general, the algorithm uses
the formula
. In general, the algorithm uses
the formula
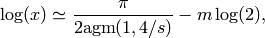
if 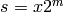 is large enough. (The result is exact to
is large enough. (The result is exact to
 bits provided that
bits provided that 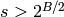 .) At low
accuracies, this function computes
.) At low
accuracies, this function computes 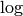 using the series
expansion near
using the series
expansion near  .
.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
Note that  -adic arguments can also be given as input,
with the convention that
-adic arguments can also be given as input,
with the convention that 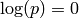 . Hence, in particular,
. Hence, in particular,
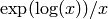 is not in general equal to
is not in general equal to  but instead to a
but instead to a 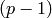 -st root of unity (or
-st root of unity (or
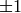 if
if 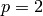 ) times a power of
) times a power of  .
.
EXAMPLES:
sage: pari(5).log()
1.60943791243410
sage: C.<i> = ComplexField()
sage: pari(i).log()
0.E-19 + 1.57079632679490*I
Logarithm of the gamma function of x.
This function returns the principal branch of the logarithm of the
gamma function of  . The function
. The function
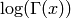 is analytic on the complex plane with
non-positive integers removed. This function can have much larger
inputs than
is analytic on the complex plane with
non-positive integers removed. This function can have much larger
inputs than 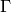 itself.
itself.
The  -adic analogue of this function is unfortunately not
implemented.
-adic analogue of this function is unfortunately not
implemented.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(100).log_gamma()
359.134205369575
matadjoint(x): adjoint matrix of x.
EXAMPLES:
sage: pari('[1,2,3; 4,5,6; 7,8,9]').matadjoint()
[-3, 6, -3; 6, -12, 6; -3, 6, -3]
sage: pari('[a,b,c; d,e,f; g,h,i]').matadjoint()
[(i*e - h*f), (-i*b + h*c), (f*b - e*c); (-i*d + g*f), i*a - g*c, -f*a + d*c; (h*d - g*e), -h*a + g*b, e*a - d*b]
Return the determinant of this matrix.
INPUT:
EXAMPLES:
sage: pari('[1,2; 3,4]').matdet(0)
-2
sage: pari('[1,2; 3,4]').matdet(1)
-2
M.matfrobenius(flag=0): Return the Frobenius form of the square
matrix M. If flag is 1, return only the elementary divisors (a list
of polynomials). If flag is 2, return a two-components vector [F,B]
where F is the Frobenius form and B is the basis change so that
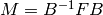 .
.
EXAMPLES:
sage: a = pari('[1,2;3,4]')
sage: a.matfrobenius()
[0, 2; 1, 5]
sage: a.matfrobenius(flag=1)
[x^2 - 5*x - 2]
sage: a.matfrobenius(2)
[[0, 2; 1, 5], [1, -1/3; 0, 1/3]]
sage: v = a.matfrobenius(2)
sage: v[0]
[0, 2; 1, 5]
sage: v[1]^(-1)*v[0]*v[1]
[1, 2; 3, 4]
We let t be the matrix of 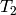 acting on modular symbols
of level 43, which was computed using
ModularSymbols(43,sign=1).T(2).matrix():
acting on modular symbols
of level 43, which was computed using
ModularSymbols(43,sign=1).T(2).matrix():
sage: t = pari('[3, -2, 0, 0; 0, -2, 0, 1; 0, -1, -2, 2; 0, -2, 0, 2]')
sage: t.matfrobenius()
[0, 0, 0, -12; 1, 0, 0, -2; 0, 1, 0, 8; 0, 0, 1, 1]
sage: t.charpoly('x')
x^4 - x^3 - 8*x^2 + 2*x + 12
sage: t.matfrobenius(1)
[x^4 - x^3 - 8*x^2 + 2*x + 12]
AUTHORS:
A.mathnf(flag=0): (upper triangular) Hermite normal form of A, basis for the lattice formed by the columns of A.
INPUT:
EXAMPLES:
sage: pari('[1,2,3; 4,5,6; 7,8,9]').mathnf()
[6, 1; 3, 1; 0, 1]
Returns the Hermite normal form if d is a multiple of the determinant
Beware that PARI’s concept of a Hermite normal form is an upper triangular matrix with the same column space as the input matrix.
INPUT:
EXAMPLES:
sage: M=matrix([[1,2,3],[4,5,6],[7,8,11]])
sage: d=M.det()
sage: pari(M).mathnfmod(d)
[6, 4, 3; 0, 1, 0; 0, 0, 1]
Note that d really needs to be a multiple of the discriminant, not just of the exponent of the cokernel:
sage: M=matrix([[1,0,0],[0,2,0],[0,0,6]])
sage: pari(M).mathnfmod(6)
[1, 0, 0; 0, 1, 0; 0, 0, 6]
sage: pari(M).mathnfmod(12)
[1, 0, 0; 0, 2, 0; 0, 0, 6]
Returns the Hermite Normal Form of M concatenated with d*Identity
Beware that PARI’s concept of a Hermite normal form is a maximal rank upper triangular matrix with the same column space as the input matrix.
INPUT:
EXAMPLES:
sage: M=matrix([[1,0,0],[0,2,0],[0,0,6]])
sage: pari(M).mathnfmodid(6)
[1, 0, 0; 0, 2, 0; 0, 0, 6]
This routine is not completely equivalent to mathnfmod:
sage: pari(M).mathnfmod(6)
[1, 0, 0; 0, 1, 0; 0, 0, 6]
Return a basis of the kernel of this matrix.
INPUT:
EXAMPLES:
sage: pari('[1,2,3;4,5,6;7,8,9]').matker()
[1; -2; 1]
With algorithm 1, even if the matrix has integer entries the kernel need not be saturated (which is weird):
sage: pari('[1,2,3;4,5,6;7,8,9]').matker(1)
[3; -6; 3]
sage: pari('matrix(3,3,i,j,i)').matker()
[-1, -1; 1, 0; 0, 1]
sage: pari('[1,2,3;4,5,6;7,8,9]*Mod(1,2)').matker()
[Mod(1, 2); Mod(0, 2); 1]
Return the integer kernel of a matrix.
This is the LLL-reduced Z-basis of the kernel of the matrix x with integral entries.
INPUT:
EXAMPLES:
sage: pari('[2,1;2,1]').matker()
[-1/2; 1]
sage: pari('[2,1;2,1]').matkerint()
[-1; 2]
This is worrisome (so be careful!):
sage: pari('[2,1;2,1]').matkerint(1)
Mat(1)
x.matsnf(flag=0): Smith normal form (i.e. elementary divisors) of the matrix x, expressed as a vector d. Binary digits of flag mean 1: returns [u,v,d] where d=u*x*v, otherwise only the diagonal d is returned, 2: allow polynomial entries, otherwise assume x is integral, 4: removes all information corresponding to entries equal to 1 in d.
EXAMPLES:
sage: pari('[1,2,3; 4,5,6; 7,8,9]').matsnf()
[0, 3, 1]
matsolve(B): Solve the linear system Mx=B for an invertible matrix M
matsolve(B) uses Gaussian elimination to solve Mx=B, where M is invertible and B is a column vector.
The corresponding pari library routine is gauss. The gp-interface name matsolve has been given preference here.
INPUT:
EXAMPLES:
sage: pari('[1,1;1,-1]').matsolve(pari('[1;0]'))
[1/2; 1/2]
Transpose of the matrix self.
EXAMPLES:
sage: pari('[1,2,3; 4,5,6; 7,8,9]').mattranspose()
[1, 4, 7; 2, 5, 8; 3, 6, 9]
modreverse(x): reverse polymod of the polymod x, if it exists.
EXAMPLES:
Return the number of columns of self.
EXAMPLES:
sage: pari('matrix(19,8)').ncols()
8
x.newtonpoly(p): Newton polygon of polynomial x with respect to the prime p.
EXAMPLES:
sage: x = pari('y^8+6*y^6-27*y^5+1/9*y^2-y+1')
sage: x.newtonpoly(3)
[1, 1, -1/3, -1/3, -1/3, -1/3, -1/3, -1/3]
nextprime(x): smallest pseudoprime = x
EXAMPLES:
sage: pari(1).nextprime()
2
sage: pari(2^100).nextprime()
1267650600228229401496703205653
nfbasis_d(x): Return a basis of the number field defined over QQ by x and its discriminant.
EXAMPLES:
sage: F = NumberField(x^3-2,'alpha')
sage: F._pari_()[0].nfbasis_d()
([1, x, x^2], -108)
sage: G = NumberField(x^5-11,'beta')
sage: G._pari_()[0].nfbasis_d()
([1, x, x^2, x^3, x^4], 45753125)
sage: pari([-2,0,0,1]).Polrev().nfbasis_d()
([1, x, x^2], -108)
nfdisc(x): Return the discriminant of the number field defined over QQ by x.
EXAMPLES:
sage: F = NumberField(x^3-2,'alpha')
sage: F._pari_()[0].nfdisc()
-108
sage: G = NumberField(x^5-11,'beta')
sage: G._pari_()[0].nfdisc()
45753125
sage: f = x^3-2
sage: f._pari_()
x^3 - 2
sage: f._pari_().nfdisc()
-108
Given an ideal I in Hermite normal form and an element x of the pari number field self, finds an element r in self such that x-r belongs to the ideal and r is small.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 5)
sage: I = k.ideal(a)
sage: kp = pari(k)
sage: kp.nfeltreduce(12, I.pari_hnf())
[2, 0]~
sage: 12 - k(kp.nfeltreduce(12, I.pari_hnf())) in I
True
Edited from the pari documentation:
nfgaloisconj(nf): list of conjugates of a root of the polynomial x=nf.pol in the same number field.
Uses a combination of Allombert’s algorithm and nfroots.
EXAMPLES:
sage: x = QQ['x'].0; nf = pari(x^2 + 2).nfinit()
sage: nf.nfgaloisconj()
[-x, x]~
sage: nf = pari(x^3 + 2).nfinit()
sage: nf.nfgaloisconj()
[x]~
sage: nf = pari(x^4 + 2).nfinit()
sage: nf.nfgaloisconj()
[-x, x]~
nfisisom(x, y): Determine if the number fields defined by x and y are isomorphic. According to the PARI documentation, this is much faster if at least one of x or y is a number field. If they are isomorphic, it returns an embedding for the generators. If not, returns 0.
EXAMPLES:
sage: F = NumberField(x^3-2,'alpha')
sage: G = NumberField(x^3-2,'beta')
sage: F._pari_().nfisisom(G._pari_())
[x]
sage: GG = NumberField(x^3-4,'gamma')
sage: F._pari_().nfisisom(GG._pari_())
[1/2*x^2]
sage: F._pari_().nfisisom(GG.pari_nf())
[1/2*x^2]
sage: F.pari_nf().nfisisom(GG._pari_()[0])
[x^2]
sage: H = NumberField(x^2-2,'alpha')
sage: F._pari_().nfisisom(H._pari_())
0
Return the roots of  in the number field self without
multiplicity.
in the number field self without
multiplicity.
EXAMPLES:
sage: y = QQ['yy'].0; _ = pari(y) # pari has variable ordering rules
sage: x = QQ['zz'].0; nf = pari(x^2 + 2).nfinit()
sage: nf.nfroots(y^2 + 2)
[Mod(-zz, zz^2 + 2), Mod(zz, zz^2 + 2)]
sage: nf = pari(x^3 + 2).nfinit()
sage: nf.nfroots(y^3 + 2)
[Mod(zz, zz^3 + 2)]
sage: nf = pari(x^4 + 2).nfinit()
sage: nf.nfroots(y^4 + 2)
[Mod(-zz, zz^4 + 2), Mod(zz, zz^4 + 2)]
nf.nfrootsof1()
number of roots of unity and primitive root of unity in the number field nf.
EXAMPLES:
sage: nf = pari('x^2 + 1').nfinit()
sage: nf.nfrootsof1()
[4, [0, 1]~]
Find all subfields of degree d of number field nf (all subfields if d is null or omitted). Result is a vector of subfields, each being given by [g,h], where g is an absolute equation and h expresses one of the roots of g in terms of the root x of the polynomial defining nf.
INPUT:
Return the number of rows of self.
EXAMPLES:
sage: pari('matrix(19,8)').nrows()
19
numbpart(x): returns the number of partitions of x.
EXAMPLES:
sage: pari(20).numbpart()
627
sage: pari(100).numbpart()
190569292
Return the number of divisors of the integer n.
EXAMPLES:
sage: pari(10).numdiv()
4
numerator(x): Returns the numerator of x.
INPUT:
OUTPUT: gen
EXAMPLES:
numtoperm(k, n): Return the permutation number k (mod n!) of n letters, where n is an integer.
INPUT:
OUTPUT:
EXAMPLES:
e.omega(): return basis for the period lattice of the elliptic curve e.
EXAMPLES:
sage: e = pari([0, -1, 1, -10, -20]).ellinit()
sage: e.omega()
[1.26920930427955, 0.634604652139777 + 1.45881661693850*I]
padicprec(x,p): Return the absolute p-adic precision of the object x.
INPUT:
OUTPUT: int
EXAMPLES:
permtonum(x): Return the ordinal (between 1 and n!) of permutation vector x. ??? Huh ??? say more. what is a perm vector. 0 to n-1 or 1-n.
INPUT:
OUTPUT:
EXAMPLES:
Return the Euler phi function of n. EXAMPLES:
sage: pari(10).phi()
4
EXAMPLES:
sage: f = pari("x^2 + y^3 + x*y")
sage: f
x^2 + y*x + y^3
sage: f.polcoeff(1)
y
sage: f.polcoeff(3)
0
sage: f.polcoeff(3, "y")
1
sage: f.polcoeff(1, "y")
x
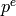 using Hensel lift.
The factors in y must be pairwise relatively prime modulo p.
using Hensel lift.
The factors in y must be pairwise relatively prime modulo p.x.polylog(m,flag=0): m-th polylogarithm of x. flag is optional, and can be 0: default, 1: D_m -modified m-th polylog of x, 2: D_m-modified m-th polylog of x, 3: P_m-modified m-th polylog of x.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
TODO: Add more explanation, copied from the PARI manual.
EXAMPLES:
sage: pari(10).polylog(3)
5.64181141475134 - 8.32820207698027*I
sage: pari(10).polylog(3,0)
5.64181141475134 - 8.32820207698027*I
sage: pari(10).polylog(3,1)
0.523778453502411
sage: pari(10).polylog(3,2)
-0.400459056163451
precision(x,n): Change the precision of x to be n, where n is a C-integer). If n is omitted, output the real precision of x.
INPUT:
OUTPUT: nothing or gen if n is omitted
EXAMPLES:
Return the number of primes less than or equal to self.
EXAMPLES:
sage: pari(7).primepi()
4
sage: pari(100).primepi()
25
sage: pari(1000).primepi()
168
sage: pari(100000).primepi()
9592
sage: pari(0).primepi()
0
sage: pari(-15).primepi()
0
sage: pari(500509).primepi()
41581
x.psi(): psi-function at x.
Return the  -function of
-function of  , i.e., the
logarithmic derivative
, i.e., the
logarithmic derivative 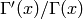 .
.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(1).psi()
-0.577215664901533
Return Python eval of self.
Note: is self is a real (type t_REAL) the result will be a RealField element of the equivalent precision; if self is a complex (type t_COMPLEX) the result will be a ComplexField element of precision the minimum precision of the real and imaginary parts.
EXAMPLES:
sage: pari('389/17').python()
389/17
sage: f = pari('(2/3)*x^3 + x - 5/7 + y'); f
2/3*x^3 + x + (y - 5/7)
sage: var('x,y')
(x, y)
sage: f.python({'x':x, 'y':y})
2/3*x^3 + x + y - 5/7
You can also use .sage, which is a psynonym:
sage: f.sage({'x':x, 'y':y})
2/3*x^3 + x + y - 5/7
Return a Python list of the PARI gens. This object must be of type t_VEC
INPUT: NoneOUTPUT:
EXAMPLES:
sage: v=pari([1,2,3,10,102,10])
sage: w = v.python_list()
sage: w
[1, 2, 3, 10, 102, 10]
sage: type(w[0])
<type 'sage.libs.pari.gen.gen'>
sage: pari("[1,2,3]").python_list()
[1, 2, 3]
Return a Python list of the PARI gens. This object must be of type t_VECSMALL, and the resulting list contains python ‘int’s
EXAMPLES:
sage: v=pari([1,2,3,10,102,10]).Vecsmall()
sage: w = v.python_list_small()
sage: w
[1, 2, 3, 10, 102, 10]
sage: type(w[0])
<type 'int'>
Computes the Hurwitz-Kronecker class number of n.
If n is large (more than 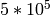 ), the result is
conditional upon GRH.
), the result is
conditional upon GRH.
EXAMPLES:
sage: pari(-10007).qfbhclassno()
77
sage: pari(-3).qfbhclassno()
1/3
random(N=2^31): Return a pseudo-random integer
between 0 and 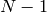 .
.
INPUT:
-N - gen, integer
OUTPUT:
EXAMPLES:
real(x): Return the real part of x.
INPUT:
OUTPUT: gen
EXAMPLES:
rnfidealdown(rnf,x): finds the intersection of the ideal x with the base field.
This is the relative HNF of the inert ideal (2) in rnf:
sage: P = pari(‘[[[1, 0]~, [0, 0]~; [0, 0]~, [1, 0]~], [[2, 0; 0, 2], [2, 0; 0, 1/2]]]’)
And this is the HNF of the inert ideal (2) in nf:
sage: rnf.rnfidealdown(P) [2, 0; 0, 2]
EXAMPLES: We construct a relative number field.
sage: f = pari('y^3+y+1')
sage: K = f.nfinit()
sage: x = pari('x'); y = pari('y')
sage: g = x^5 - x^2 + y
sage: L = K.rnfinit(g)
round(x,estimate=False): If x is a real number, returns x rounded to the nearest integer (rounding up). If the optional argument estimate is True, also returns the binary exponent e of the difference between the original and the rounded value (the “fractional part”) (this is the integer ceiling of log_2(error)).
When x is a general PARI object, this function returns the result of rounding every coefficient at every level of PARI object. Note that this is different than what the truncate function does (see the example below).
One use of round is to get exact results after a long approximate computation, when theory tells you that the coefficients must be integers.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari('1.5').round()
2
sage: pari('1.5').round(True)
(2, -1)
sage: pari('1.5 + 2.1*I').round()
2 + 2*I
sage: pari('1.0001').round(True)
(1, -14)
sage: pari('(2.4*x^2 - 1.7)/x').round()
(2*x^2 - 2)/x
sage: pari('(2.4*x^2 - 1.7)/x').truncate()
2.40000000000000*x
Return Python eval of self.
Note: is self is a real (type t_REAL) the result will be a RealField element of the equivalent precision; if self is a complex (type t_COMPLEX) the result will be a ComplexField element of precision the minimum precision of the real and imaginary parts.
EXAMPLES:
sage: pari('389/17').python()
389/17
sage: f = pari('(2/3)*x^3 + x - 5/7 + y'); f
2/3*x^3 + x + (y - 5/7)
sage: var('x,y')
(x, y)
sage: f.python({'x':x, 'y':y})
2/3*x^3 + x + y - 5/7
You can also use .sage, which is a psynonym:
sage: f.sage({'x':x, 'y':y})
2/3*x^3 + x + y - 5/7
serreverse(f): reversion of the power series f.
If f(t) is a series in t with valuation 1, find the series g(t) such that g(f(t)) = t.
EXAMPLES:
sage: f = pari('x+x^2+x^3+O(x^4)'); f
x + x^2 + x^3 + O(x^4)
sage: g = f.serreverse(); g
x - x^2 + x^3 + O(x^4)
sage: f.subst('x',g)
x + O(x^4)
sage: g.subst('x',f)
x + O(x^4)
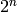 .
.simplify(x): Simplify the object x as much as possible, and return the result.
A complex or quadratic number whose imaginary part is an exact 0 (i.e., not an approximate one such as O(3) or 0.E-28) is converted to its real part, and a a polynomial of degree 0 is converted to its constant term. Simplification occurs recursively.
This function is useful before using arithmetic functions, which expect integer arguments:
EXAMPLES:
sage: y = pari('y')
sage: x = pari('9') + y - y
sage: x
9
sage: x.type()
't_POL'
sage: x.factor()
matrix(0,2)
sage: pari('9').factor()
Mat([3, 2])
sage: x.simplify()
9
sage: x.simplify().factor()
Mat([3, 2])
sage: x = pari('1.5 + 0*I')
sage: x.type()
't_COMPLEX'
sage: x.simplify()
1.50000000000000
sage: y = x.simplify()
sage: y.type()
't_REAL'
x.sin(): The sine of x.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(1).sin()
0.841470984807897
sage: C.<i> = ComplexField()
sage: pari(1+i).sin()
1.29845758141598 + 0.634963914784736*I
The hyperbolic sine function.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(0).sinh()
0.E-19
sage: C.<i> = ComplexField()
sage: pari(1+i).sinh()
0.634963914784736 + 1.29845758141598*I
sizebyte(x): Return the total number of bytes occupied by the complete tree of the object x. Note that this number depends on whether the computer is 32-bit or 64-bit (see examples).
INPUT:
OUTPUT: int (a Python int)
EXAMPLES:
sage: pari('1').sizebyte()
12 # 32-bit
24 # 64-bit
sage: pari('10').sizebyte()
12 # 32-bit
24 # 64-bit
sage: pari('10000000000000').sizebyte()
16 # 32-bit
24 # 64-bit
sage: pari('10^100').sizebyte()
52 # 32-bit
64 # 64-bit
sage: pari('x').sizebyte()
36 # 32-bit
72 # 64-bit
sage: pari('x^20').sizebyte()
264 # 32-bit
528 # 64-bit
sage: pari('[x, 10^100]').sizebyte()
100 # 32-bit
160 # 64-bit
sizedigit(x): Return a quick estimate for the maximal number of decimal digits before the decimal point of any component of x.
INPUT:
OUTPUT:
EXAMPLES:
sage: x = pari('10^100')
sage: x.Str().length()
101
sage: x.sizedigit()
101
Note that digits after the decimal point are ignored.
sage: x = pari('1.234')
sage: x
1.23400000000000
sage: x.sizedigit()
1
The estimate can be one too big:
sage: pari('7234.1').sizedigit()
4
sage: pari('9234.1').sizedigit()
5
x.sqr(): square of x. Faster than, and most of the time (but not always - see the examples) identical to x*x.
EXAMPLES:
sage: pari(2).sqr()
4
For  -adic numbers, x.sqr() may not be identical to x*x
(squaring a
-adic numbers, x.sqr() may not be identical to x*x
(squaring a  -adic number increases its precision):
-adic number increases its precision):
sage: pari("1+O(2^5)").sqr()
1 + O(2^6)
sage: pari("1+O(2^5)")*pari("1+O(2^5)")
1 + O(2^5)
However:
sage: x = pari("1+O(2^5)"); x*x
1 + O(2^6)
x.sqrt(precision): The square root of x.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(2).sqrt()
1.41421356237310
x.sqrtn(n): return the principal branch of the n-th root of x,
i.e., the one such that
![\arg(\sqrt(x)) \in ]-\pi/n, \pi/n]](../../../_images/math/71b81df232e0aae34a0775e643e2fb123d08c46c.png) . Also returns a second
argument which is a suitable root of unity allowing one to recover
all the other roots. If it was not possible to find such a number,
then this second return value is 0. If the argument is present and
no square root exists, return 0 instead of raising an error.
. Also returns a second
argument which is a suitable root of unity allowing one to recover
all the other roots. If it was not possible to find such a number,
then this second return value is 0. If the argument is present and
no square root exists, return 0 instead of raising an error.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
Note
intmods (modulo a prime) and  -adic numbers are
allowed as arguments.
-adic numbers are
allowed as arguments.
INPUT:
OUTPUT:
EXAMPLES:
sage: s, z = pari(2).sqrtn(5)
sage: z
0.309016994374947 + 0.951056516295154*I
sage: s
1.14869835499704
sage: s^5
2.00000000000000
sage: z^5
1.00000000000000 + 5.42101086 E-19*I # 32-bit
1.00000000000000 + 4.87890977618477 E-19*I # 64-bit
sage: (s*z)^5
2.00000000000000 + 1.409462824 E-18*I # 32-bit
2.00000000000000 + 7.58941520739853 E-19*I # 64-bit
EXAMPLES:
sage: x = pari("x"); y = pari("y")
sage: f = pari('x^3 + 17*x + 3')
sage: f.subst(x, y)
y^3 + 17*y + 3
sage: f.subst(x, "z")
z^3 + 17*z + 3
sage: f.subst(x, "z")^2
z^6 + 34*z^4 + 6*z^3 + 289*z^2 + 102*z + 9
sage: f.subst(x, "x+1")
x^3 + 3*x^2 + 20*x + 21
sage: f.subst(x, "xyz")
xyz^3 + 17*xyz + 3
sage: f.subst(x, "xyz")^2
xyz^6 + 34*xyz^4 + 6*xyz^3 + 289*xyz^2 + 102*xyz + 9
Return the sum of the divisors of  .
.
EXAMPLES:
sage: pari(10).sumdiv()
18
Return the sum of the k-th powers of the divisors of n.
EXAMPLES:
sage: pari(10).sumdivk(2)
130
x.tan() - tangent of x
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(2).tan()
-2.18503986326152
sage: C.<i> = ComplexField()
sage: pari(i).tan()
0.E-19 + 0.761594155955765*I
x.tanh() - hyperbolic tangent of x
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(1).tanh()
0.761594155955765
sage: C.<i> = ComplexField()
sage: pari(i).tanh()
0.E-19 + 1.55740772465490*I
teichmuller(x): teichmuller character of p-adic number x.
This is the unique 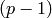 -st root of unity congruent to
-st root of unity congruent to
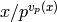 modulo
modulo  .
.
EXAMPLES:
sage: pari('2+O(7^5)').teichmuller()
2 + 4*7 + 6*7^2 + 3*7^3 + O(7^5)
q.theta(z): Jacobi sine theta-function.
If  or
or  is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
is an exact argument, it is first
converted to a real or complex number using the optional parameter
precision (in bits). If the arguments are inexact (e.g. real), the
smallest of their precisions is used in the computation, and the
parameter precision is ignored.
EXAMPLES:
sage: pari(0.5).theta(2)
1.63202590295260
q.thetanullk(k): return the k-th derivative at z=0 of theta(q,z).
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
EXAMPLES:
sage: pari(0.5).thetanullk(1)
0.548978532560341
Return the trace of this PARI object.
EXAMPLES:
sage: pari('[1,2; 3,4]').trace()
5
truncate(x,estimate=False): Return the truncation of x. If estimate is True, also return the number of error bits.
When x is in the real numbers, this means that the part after the decimal point is chopped away, e is the binary exponent of the difference between the original and truncated value (the “fractional part”). If x is a rational function, the result is the integer part (Euclidean quotient of numerator by denominator) and if requested the error estimate is 0.
When truncate is applied to a power series (in X), it transforms it
into a polynomial or a rational function with denominator a power
of X, by chopping away the 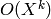 . Similarly, when
applied to a p-adic number, it transforms it into an integer or a
rational number by chopping away the
. Similarly, when
applied to a p-adic number, it transforms it into an integer or a
rational number by chopping away the 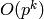 .
.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari('(x^2+1)/x').round()
(x^2 + 1)/x
sage: pari('(x^2+1)/x').truncate()
x
sage: pari('1.043').truncate()
1
sage: pari('1.043').truncate(True)
(1, -5)
sage: pari('1.6').truncate()
1
sage: pari('1.6').round()
2
sage: pari('1/3 + 2 + 3^2 + O(3^3)').truncate()
34/3
sage: pari('sin(x+O(x^10))').truncate()
1/362880*x^9 - 1/5040*x^7 + 1/120*x^5 - 1/6*x^3 + x
sage: pari('sin(x+O(x^10))').round() # each coefficient has abs < 1
x + O(x^10)
Return the Pari type of self as a string.
Note
In Cython, it is much faster to simply use typ(self.g) for checking Pari types.
EXAMPLES:
sage: pari(7).type()
't_INT'
sage: pari('x').type()
't_POL'
valuation(x,p): Return the valuation of x with respect to p.
The valuation is the highest exponent of p dividing x.
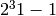 on 32-bit machines or
on 32-bit machines or
 on 64-bit machines if x is an exact
object. If x is a p-adic number or power series, the result
is the exponent of the zero.
on 64-bit machines if x is an exact
object. If x is a p-adic number or power series, the result
is the exponent of the zero.INPUT:
OUTPUT:
EXAMPLES:
sage: pari(9).valuation(3)
2
sage: pari(9).valuation(9)
1
sage: x = pari(9).Mod(27); x.valuation(3)
2
sage: pari('5/3').valuation(3)
-1
sage: pari('9 + 3*x + 15*x^2').valuation(3)
1
sage: pari([9,3,15]).valuation(3)
1
sage: pari('9 + 3*x + 15*x^2 + O(x^5)').valuation(3)
1
sage: pari('x^2*(x+1)^3').valuation(pari('x+1'))
3
sage: pari('x + O(x^5)').valuation('x')
1
sage: pari('2*x^2 + O(x^5)').valuation('x')
2
sage: pari(0).valuation(3)
2147483647 # 32-bit
9223372036854775807 # 64-bit
variable(x): Return the main variable of the object x, or p if x is a p-adic number.
This function raises a TypeError exception on scalars, i.e., on objects with no variable associated to them.
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari('x^2 + x -2').variable()
x
sage: pari('1+2^3 + O(2^5)').variable()
2
sage: pari('x+y0').variable()
x
sage: pari('y0+z0').variable()
y0
self.vecextract(y,z): extraction of the components of the matrix or vector x according to y and z. If z is omitted, y designates columns, otherwise y corresponds to rows and z to columns. y and z can be vectors (of indices), strings (indicating ranges as in”1..10”) or masks (integers whose binary representation indicates the indices to extract, from left to right 1, 2, 4, 8, etc.)
Note
This function uses the PARI row and column indexing, so the first row or column is indexed by 1 instead of 0.
x.weber(flag=0): One of Weber’s f functions of x. flag is optional,
and can be 0: default, function
f(x)=exp(-i*Pi/24)*eta((x+1)/2)/eta(x) such that
 , 1: function f1(x)=eta(x/2)/eta(x)
such that
, 1: function f1(x)=eta(x/2)/eta(x)
such that  , 2: function
f2(x)=sqrt(2)*eta(2*x)/eta(x) such that
, 2: function
f2(x)=sqrt(2)*eta(2*x)/eta(x) such that
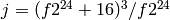 .
.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
TODO: Add further explanation from PARI manual.
EXAMPLES:
sage: C.<i> = ComplexField()
sage: pari(i).weber()
1.18920711500272 + 0.E-19*I
sage: pari(i).weber(1)
1.09050773266526 + 0.E-19*I
sage: pari(i).weber(2)
1.09050773266526 + 0.E-19*I
Returns u,v,d such that d=gcd(x,y) and u*x+v*y=d.
EXAMPLES:
sage: pari(10).xgcd(15)
(5, -1, 1)
zeta(s): zeta function at s with s a complex or a p-adic number.
If  is a complex number, this is the Riemann zeta
function
is a complex number, this is the Riemann zeta
function 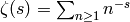 , computed either
using the Euler-Maclaurin summation formula (if
, computed either
using the Euler-Maclaurin summation formula (if  is not
an integer), or using Bernoulli numbers (if
is not
an integer), or using Bernoulli numbers (if  is a
negative integer or an even nonnegative integer), or using modular
forms (if
is a
negative integer or an even nonnegative integer), or using modular
forms (if  is an odd nonnegative integer).
is an odd nonnegative integer).
If  is a
is a  -adic number, this is the
Kubota-Leopoldt zeta function, i.e. the unique continuous
-adic number, this is the
Kubota-Leopoldt zeta function, i.e. the unique continuous
 -adic function on the
-adic function on the  -adic integers that
interpolates the values of
-adic integers that
interpolates the values of 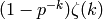 at negative
integers
at negative
integers  such that
such that 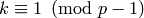 if
if
 is odd, and at odd
is odd, and at odd  if
if 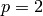 .
.
If  is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If
is an exact argument, it is first converted to a
real or complex number using the optional parameter precision (in
bits). If  is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
is inexact (e.g. real), its own precision is
used in the computation, and the parameter precision is ignored.
INPUT:
OUTPUT:
EXAMPLES:
sage: pari(2).zeta()
1.64493406684823
sage: x = RR(pi)^2/6
sage: pari(x)
1.64493406684823
sage: pari(3).zeta()
1.20205690315959
sage: pari('1+5*7+2*7^2+O(7^3)').zeta()
4*7^-2 + 5*7^-1 + O(7^0)
Return a primitive root modulo self, whenever it exists.
This is a generator of the group 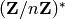 , whenever
this group is cyclic, i.e. if
, whenever
this group is cyclic, i.e. if 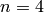 or
or 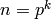 or
or
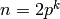 , where
, where  is an odd prime and
is an odd prime and  is a natural number.
is a natural number.
INPUT:
OUTPUT: gen
EXAMPLES:
sage: pari(4).znprimroot()
Mod(3, 4)
sage: pari(10007^3).znprimroot()
Mod(5, 1002101470343)
sage: pari(2*109^10).znprimroot()
Mod(236736367459211723407, 473472734918423446802)
Change the PARI scratch stack space to the given size.
The main application of this command is that you’ve done some individual PARI computation that used a lot of stack space. As a result the PARI stack may have doubled several times and is now quite large. That object you computed is copied off to the heap, but the PARI stack is never automatically shrunk back down. If you call this function you can shrink it back down.
If you set this too small then it will automatically be increased if it is exceeded, which could make some calculations initially slower (since they have to be redone until the stack is big enough).
INPUT:
EXAMPLES:
sage: get_memory_usage() # random output
'122M+'
sage: a = pari('2^100000000')
sage: get_memory_usage() # random output
'157M+'
sage: del a
sage: get_memory_usage() # random output
'145M+'
Hey, I want my memory back!
sage: sage.libs.pari.gen.init_pari_stack()
sage: get_memory_usage() # random output
'114M+'
Ahh, that’s better.
Convert from precision expressed in bits to pari real precision expressed in words. Note: this rounds up to the nearest word, adjusts for the two codewords of a pari real, and is architecture-dependent.
EXAMPLES:
sage: import sage.libs.pari.gen as gen
sage: gen.prec_bits_to_words(70)
5 # 32-bit
4 # 64-bit
sage: [(32*n,gen.prec_bits_to_words(32*n)) for n in range(1,9)]
[(32, 3), (64, 4), (96, 5), (128, 6), (160, 7), (192, 8), (224, 9), (256, 10)] # 32-bit
[(32, 3), (64, 3), (96, 4), (128, 4), (160, 5), (192, 5), (224, 6), (256, 6)] # 64-bit
Convert from precision expressed in bits to precision expressed in decimal.
EXAMPLES:
sage: import sage.libs.pari.gen as gen
sage: gen.prec_bits_to_dec(53)
15
sage: [(32*n,gen.prec_bits_to_dec(32*n)) for n in range(1,9)]
[(32, 9),
(64, 19),
(96, 28),
(128, 38),
(160, 48),
(192, 57),
(224, 67),
(256, 77)]
Convert from precision expressed in bits to pari real precision expressed in words. Note: this rounds up to the nearest word, adjusts for the two codewords of a pari real, and is architecture-dependent.
EXAMPLES:
sage: import sage.libs.pari.gen as gen
sage: gen.prec_bits_to_words(70)
5 # 32-bit
4 # 64-bit
sage: [(32*n,gen.prec_bits_to_words(32*n)) for n in range(1,9)]
[(32, 3), (64, 4), (96, 5), (128, 6), (160, 7), (192, 8), (224, 9), (256, 10)] # 32-bit
[(32, 3), (64, 3), (96, 4), (128, 4), (160, 5), (192, 5), (224, 6), (256, 6)] # 64-bit
Convert from precision expressed in decimal to precision expressed in bits.
EXAMPLES:
sage: import sage.libs.pari.gen as gen
sage: gen.prec_dec_to_bits(15)
49
sage: [(n,gen.prec_dec_to_bits(n)) for n in range(10,100,10)]
[(10, 33),
(20, 66),
(30, 99),
(40, 132),
(50, 166),
(60, 199),
(70, 232),
(80, 265),
(90, 298)]
Convert from precision expressed in decimal to precision expressed in words. Note: this rounds up to the nearest word, adjusts for the two codewords of a pari real, and is architecture-dependent.
EXAMPLES:
sage: import sage.libs.pari.gen as gen
sage: gen.prec_dec_to_words(38)
6 # 32-bit
4 # 64-bit
sage: [(n,gen.prec_dec_to_words(n)) for n in range(10,90,10)]
[(10, 4), (20, 5), (30, 6), (40, 7), (50, 8), (60, 9), (70, 10), (80, 11)] # 32-bit
[(10, 3), (20, 4), (30, 4), (40, 5), (50, 5), (60, 6), (70, 6), (80, 7)] # 64-bit
Convert from pari real precision expressed in words to precision expressed in bits. Note: this adjusts for the two codewords of a pari real, and is architecture-dependent.
EXAMPLES:
sage: import sage.libs.pari.gen as gen
sage: gen.prec_words_to_bits(10)
256 # 32-bit
512 # 64-bit
sage: [(n,gen.prec_words_to_bits(n)) for n in range(3,10)]
[(3, 32), (4, 64), (5, 96), (6, 128), (7, 160), (8, 192), (9, 224)] # 32-bit
[(3, 64), (4, 128), (5, 192), (6, 256), (7, 320), (8, 384), (9, 448)] # 64-bit
Convert from precision expressed in words to precision expressed in decimal. Note: this adjusts for the two codewords of a pari real, and is architecture-dependent.
EXAMPLES:
sage: import sage.libs.pari.gen as gen
sage: gen.prec_words_to_dec(5)
28 # 32-bit
57 # 64-bit
sage: [(n,gen.prec_words_to_dec(n)) for n in range(3,10)]
[(3, 9), (4, 19), (5, 28), (6, 38), (7, 48), (8, 57), (9, 67)] # 32-bit
[(3, 19), (4, 38), (5, 57), (6, 77), (7, 96), (8, 115), (9, 134)] # 64-bit
INPUT:
OUTPUT: a Python list of Python ints