Maxima is a free GPL’d general purpose computer algebra system
whose development started in 1968 at MIT. It contains symbolic
manipulation algorithms, as well as implementations of special
functions, including elliptic functions and generalized
hypergeometric functions. Moreover, Maxima has implementations of
many functions relating to the invariant theory of the symmetric
group 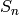 . (However, the commands for group invariants,
and the corresponding Maxima documentation, are in French.) For many
links to Maxima documentation see
http://maxima.sourceforge.net/docs.shtml/.
. (However, the commands for group invariants,
and the corresponding Maxima documentation, are in French.) For many
links to Maxima documentation see
http://maxima.sourceforge.net/docs.shtml/.
AUTHORS:
If the string “error” (case insensitive) occurs in the output of anything from Maxima, a RuntimeError exception is raised.
EXAMPLES: We evaluate a very simple expression in Maxima.
sage: maxima('3 * 5')
15
We factor 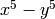 in Maxima in several different ways.
The first way yields a Maxima object.
in Maxima in several different ways.
The first way yields a Maxima object.
sage: F = maxima.factor('x^5 - y^5')
sage: F
-(y-x)*(y^4+x*y^3+x^2*y^2+x^3*y+x^4)
sage: type(F)
<class 'sage.interfaces.maxima.MaximaElement'>
Note that Maxima objects can also be displayed using “ASCII art”; to see a normal linear representation of any Maxima object x. Just use the print command: use str(x).
sage: print F
4 3 2 2 3 4
- (y - x) (y + x y + x y + x y + x )
You can always use repr(x) to obtain the linear representation of an object. This can be useful for moving maxima data to other systems.
sage: repr(F)
'-(y-x)*(y^4+x*y^3+x^2*y^2+x^3*y+x^4)'
sage: F.str()
'-(y-x)*(y^4+x*y^3+x^2*y^2+x^3*y+x^4)'
The maxima.eval command evaluates an expression in maxima and returns the result as a string not a maxima object.
sage: print maxima.eval('factor(x^5 - y^5)')
-(y-x)*(y^4+x*y^3+x^2*y^2+x^3*y+x^4)
We can create the polynomial  as a Maxima polynomial,
then call the factor method on it. Notice that the notation
f.factor() is consistent with how the rest of Sage
works.
as a Maxima polynomial,
then call the factor method on it. Notice that the notation
f.factor() is consistent with how the rest of Sage
works.
sage: f = maxima('x^5 - y^5')
sage: f^2
(x^5-y^5)^2
sage: f.factor()
-(y-x)*(y^4+x*y^3+x^2*y^2+x^3*y+x^4)
Control-C interruption works well with the maxima interface, because of the excellent implementation of maxima. For example, try the following sum but with a much bigger range, and hit control-C.
sage: maxima('sum(1/x^2, x, 1, 10)')
1968329/1270080
We follow the tutorial at http://maxima.sourceforge.net/docs/intromax/.
sage: maxima('1/100 + 1/101')
201/10100
sage: a = maxima('(1 + sqrt(2))^5'); a
(sqrt(2)+1)^5
sage: a.expand()
3*2^(7/2)+5*sqrt(2)+41
sage: a = maxima('(1 + sqrt(2))^5')
sage: float(a)
82.012193308819747
sage: a.numer()
82.01219330881975
sage: maxima.eval('fpprec : 100')
'100'
sage: a.bfloat()
8.20121933088197564152489730020812442785204843859314941221237124017312418754011041266612384955016056b1
sage: maxima('100!')
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
sage: f = maxima('(x + 3*y + x^2*y)^3')
sage: f.expand()
x^6*y^3+9*x^4*y^3+27*x^2*y^3+27*y^3+3*x^5*y^2+18*x^3*y^2+27*x*y^2+3*x^4*y+9*x^2*y+x^3
sage: f.subst('x=5/z')
(5/z+25*y/z^2+3*y)^3
sage: g = f.subst('x=5/z')
sage: h = g.ratsimp(); h
(27*y^3*z^6+135*y^2*z^5+(675*y^3+225*y)*z^4+(2250*y^2+125)*z^3+(5625*y^3+1875*y)*z^2+9375*y^2*z+15625*y^3)/z^6
sage: h.factor()
(3*y*z^2+5*z+25*y)^3/z^6
sage: eqn = maxima(['a+b*c=1', 'b-a*c=0', 'a+b=5'])
sage: s = eqn.solve('[a,b,c]'); s
[[a=(25*sqrt(79)*%i+25)/(6*sqrt(79)*%i-34),b=(5*sqrt(79)*%i+5)/(sqrt(79)*%i+11),c=(sqrt(79)*%i+1)/10],[a=(25*sqrt(79)*%i-25)/(6*sqrt(79)*%i+34),b=(5*sqrt(79)*%i-5)/(sqrt(79)*%i-11),c=-(sqrt(79)*%i-1)/10]]
Here is an example of solving an algebraic equation:
sage: maxima('x^2+y^2=1').solve('y')
[y=-sqrt(1-x^2),y=sqrt(1-x^2)]
sage: maxima('x^2 + y^2 = (x^2 - y^2)/sqrt(x^2 + y^2)').solve('y')
[y=-sqrt((-y^2-x^2)*sqrt(y^2+x^2)+x^2),y=sqrt((-y^2-x^2)*sqrt(y^2+x^2)+x^2)]
You can even nicely typeset the solution in latex:
sage: latex(s)
\left[ \left[ a={{25\,\sqrt{79}\,i+25}\over{6\,\sqrt{79}\,i-34}} , b={{5\,\sqrt{79}\,i+5}\over{\sqrt{79}\,i+11}} , c={{\sqrt{79}\,i+1 }\over{10}} \right] , \left[ a={{25\,\sqrt{79}\,i-25}\over{6\, \sqrt{79}\,i+34}} , b={{5\,\sqrt{79}\,i-5}\over{\sqrt{79}\,i-11}} , c=-{{\sqrt{79}\,i-1}\over{10}} \right] \right]
To have the above appear onscreen via xdvi, type view(s). (TODO: For OS X should create pdf output and use preview instead?)
sage: e = maxima('sin(u + v) * cos(u)^3'); e
cos(u)^3*sin(v+u)
sage: f = e.trigexpand(); f
cos(u)^3*(cos(u)*sin(v)+sin(u)*cos(v))
sage: f.trigreduce()
(sin(v+4*u)+sin(v-2*u))/8+(3*sin(v+2*u)+3*sin(v))/8
sage: w = maxima('3 + k*%i')
sage: f = w^2 + maxima('%e')^w
sage: f.realpart()
%e^3*cos(k)-k^2+9
sage: f = maxima('x^3 * %e^(k*x) * sin(w*x)'); f
x^3*%e^(k*x)*sin(w*x)
sage: f.diff('x')
k*x^3*%e^(k*x)*sin(w*x)+3*x^2*%e^(k*x)*sin(w*x)+w*x^3*%e^(k*x)*cos(w*x)
sage: f.integrate('x')
(((k*w^6+3*k^3*w^4+3*k^5*w^2+k^7)*x^3+(3*w^6+3*k^2*w^4-3*k^4*w^2-3*k^6)*x^2+(-18*k*w^4-12*k^3*w^2+6*k^5)*x-6*w^4+36*k^2*w^2-6*k^4)*%e^(k*x)*sin(w*x)+((-w^7-3*k^2*w^5-3*k^4*w^3-k^6*w)*x^3+(6*k*w^5+12*k^3*w^3+6*k^5*w)*x^2+(6*w^5-12*k^2*w^3-18*k^4*w)*x-24*k*w^3+24*k^3*w)*%e^(k*x)*cos(w*x))/(w^8+4*k^2*w^6+6*k^4*w^4+4*k^6*w^2+k^8)
sage: f = maxima('1/x^2')
sage: f.integrate('x', 1, 'inf')
1
sage: g = maxima('f/sinh(k*x)^4')
sage: g.taylor('x', 0, 3)
f/(k^4*x^4)-2*f/(3*k^2*x^2)+11*f/45-62*k^2*f*x^2/945
sage: maxima.taylor('asin(x)','x',0, 10)
x+x^3/6+3*x^5/40+5*x^7/112+35*x^9/1152
We illustrate computing with the matrix whose 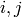 entry
is
entry
is 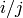 , for
, for 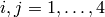 .
.
sage: f = maxima.eval('f[i,j] := i/j')
sage: A = maxima('genmatrix(f,4,4)'); A
matrix([1,1/2,1/3,1/4],[2,1,2/3,1/2],[3,3/2,1,3/4],[4,2,4/3,1])
sage: A.determinant()
0
sage: A.echelon()
matrix([1,1/2,1/3,1/4],[0,0,0,0],[0,0,0,0],[0,0,0,0])
sage: A.eigenvalues()
[[0,4],[3,1]]
sage: A.eigenvectors()
[[[0,4],[3,1]],[[[1,0,0,-4],[0,1,0,-2],[0,0,1,-4/3]],[[1,2,3,4]]]]
We can also compute the echelon form in Sage:
sage: B = matrix(QQ, A)
sage: B.echelon_form()
[ 1 1/2 1/3 1/4]
[ 0 0 0 0]
[ 0 0 0 0]
[ 0 0 0 0]
sage: B.charpoly('x').factor()
(x - 4) * x^3
We illustrate Laplace transforms:
sage: _ = maxima.eval("f(t) := t*sin(t)")
sage: maxima("laplace(f(t),t,s)")
2*s/(s^2+1)^2
sage: maxima("laplace(delta(t-3),t,s)") #Dirac delta function
%e^-(3*s)
sage: _ = maxima.eval("f(t) := exp(t)*sin(t)")
sage: maxima("laplace(f(t),t,s)")
1/(s^2-2*s+2)
sage: _ = maxima.eval("f(t) := t^5*exp(t)*sin(t)")
sage: maxima("laplace(f(t),t,s)")
360*(2*s-2)/(s^2-2*s+2)^4-480*(2*s-2)^3/(s^2-2*s+2)^5+120*(2*s-2)^5/(s^2-2*s+2)^6
sage: print maxima("laplace(f(t),t,s)")
3 5
360 (2 s - 2) 480 (2 s - 2) 120 (2 s - 2)
--------------- - --------------- + ---------------
2 4 2 5 2 6
(s - 2 s + 2) (s - 2 s + 2) (s - 2 s + 2)
sage: maxima("laplace(diff(x(t),t),t,s)")
s*'laplace(x(t),t,s)-x(0)
sage: maxima("laplace(diff(x(t),t,2),t,s)")
-?%at('diff(x(t),t,1),t=0)+s^2*'laplace(x(t),t,s)-x(0)*s
It is difficult to read some of these without the 2d representation:
sage: print maxima("laplace(diff(x(t),t,2),t,s)")
!
d ! 2
- -- (x(t))! + s laplace(x(t), t, s) - x(0) s
dt !
!t = 0
Even better, use view(maxima("laplace(diff(x(t),t,2),t,s)")) to see a typeset version.
A continued fraction 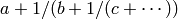 is
represented in maxima by the list
is
represented in maxima by the list ![[a, b, c, \ldots]](../../_images/math/b881f30726eb64ad5b49b0b0b59a1ef3ecb3dfd4.png) .
.
sage: maxima("cf((1 + sqrt(5))/2)")
[1,1,1,1,2]
sage: maxima("cf ((1 + sqrt(341))/2)")
[9,1,2,1,2,1,17,1,2,1,2,1,17,1,2,1,2,1,17,2]
In this section we illustrate calculations that would be awkward to do (as far as I know) in non-symbolic computer algebra systems like MAGMA or GAP.
We compute the gcd of 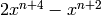 and
and
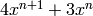 for arbitrary
for arbitrary  .
.
sage: f = maxima('2*x^(n+4) - x^(n+2)')
sage: g = maxima('4*x^(n+1) + 3*x^n')
sage: f.gcd(g)
x^n
You can plot 3d graphs (via gnuplot):
sage: maxima('plot3d(x^2-y^2, [x,-2,2], [y,-2,2], [grid,12,12])') # not tested
[displays a 3 dimensional graph]
You can formally evaluate sums (note the nusum command):
sage: S = maxima('nusum(exp(1+2*i/n),i,1,n)')
sage: print S
2/n + 3 2/n + 1
%e %e
----------------------- - -----------------------
1/n 1/n 1/n 1/n
(%e - 1) (%e + 1) (%e - 1) (%e + 1)
We formally compute the limit as 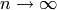 of
of
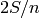 as follows:
as follows:
sage: T = S*maxima('2/n')
sage: T.tlimit('n','inf')
%e^3-%e
Obtaining digits of 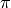 :
:
sage: maxima.eval('fpprec : 100')
'100'
sage: maxima(pi).bfloat()
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068b0
Defining functions in maxima:
sage: maxima.eval('fun[a] := a^2')
'fun[a]:=a^2'
sage: maxima('fun[10]')
100
Unfortunately maxima doesn’t seem to have a non-interactive mode, which is needed for the Sage interface. If any Sage call leads to maxima interactively answering questions, then the questions can’t be answered and the maxima session may hang. See the discussion at http://www.ma.utexas.edu/pipermail/maxima/2005/011061.html for some ideas about how to fix this problem. An example that illustrates this problem is maxima.eval('integrate (exp(a*x), x, 0, inf)').
To TeX a maxima object do this:
sage: latex(maxima('sin(u) + sinh(v^2)'))
\sinh v^2+\sin u
Here’s another example:
sage: g = maxima('exp(3*%i*x)/(6*%i) + exp(%i*x)/(2*%i) + c')
sage: latex(g)
-{{i\,e^{3\,i\,x}}\over{6}}-{{i\,e^{i\,x}}\over{2}}+c
The MAXIMA interface reads in even very long input (using files) in a robust manner, as long as you are creating a new object.
Note
Using maxima.eval for long input is much less robust, and is not recommended.
sage: t = '"%s"'%10^10000 # ten thousand character string.
sage: a = maxima(t)
TESTS: This working tests that a subtle bug has been fixed:
sage: f = maxima.function('x','gamma(x)')
sage: g = f(1/7)
sage: g
gamma(1/7)
sage: del f
sage: maxima(sin(x))
sin(x)
This tests to make sure we handle the case where Maxima asks if an expression is positive or zero.
sage: var('Ax,Bx,By')
(Ax, Bx, By)
sage: t = -Ax*sin(sqrt(Ax^2)/2)/(sqrt(Ax^2)*sqrt(By^2 + Bx^2))
sage: t.limit(Ax=0,dir='above')
0
A long complicated input expression:
sage: maxima._eval_line('((((((((((0) + ((1) / ((n0) ^ (0)))) + ((1) / ((n1) ^ (1)))) + ((1) / ((n2) ^ (2)))) + ((1) / ((n3) ^ (3)))) + ((1) / ((n4) ^ (4)))) + ((1) / ((n5) ^ (5)))) + ((1) / ((n6) ^ (6)))) + ((1) / ((n7) ^ (7)))) + ((1) / ((n8) ^ (8)))) + ((1) / ((n9) ^ (9)));')
'1/n9^9+1/n8^8+1/n7^7+1/n6^6+1/n5^5+1/n4^4+1/n3^3+1/n2^2+1/n1+1'
Bases: sage.interfaces.expect.Expect
Interface to the Maxima interpreter.
Change Maxima’s current working directory.
EXAMPLES:
sage: maxima.chdir('/')
Clear the variable named var.
EXAMPLES:
sage: maxima.set('xxxxx', '2')
sage: maxima.get('xxxxx')
'2'
sage: maxima.clear('xxxxx')
sage: maxima.get('xxxxx')
'xxxxx'
Return all commands that complete the command starting with the string s. This is like typing s[tab] in the Maxima interpreter.
EXAMPLES:
sage: sorted(maxima.completions('gc', verbose=False))
['gcd', 'gcdex', 'gcfactor', 'gcprint', 'gctime']
Start the interactive Maxima console. This is a completely separate maxima session from this interface. To interact with this session, you should instead use maxima.interact().
EXAMPLES:
sage: maxima.console() # not tested (since we can't)
Maxima 5.13.0 http://maxima.sourceforge.net
Using Lisp CLISP 2.41 (2006-10-13)
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
This is a development version of Maxima. The function bug_report()
provides bug reporting information.
(%i1)
sage: maxima.interact() # this is not tested either
--> Switching to Maxima <--
maxima: 2+2
4
maxima:
--> Exiting back to Sage <--
Returns the amount of CPU time that this Maxima session has used. If var{t} is not None, then it returns the difference between the current CPU time and var{t}.
Solves a 1st or 2nd order ordinary differential equation (ODE) in two variables, possibly with initial conditions.
INPUT:
EXAMPLES:
sage: maxima.de_solve('diff(y,x,2) + 3*x = y', ['x','y'], [1,1,1])
y=3*x-2*%e^(x-1)
sage: maxima.de_solve('diff(y,x,2) + 3*x = y', ['x','y'])
y=%k1*%e^x+%k2*%e^-x+3*x
sage: maxima.de_solve('diff(y,x) + 3*x = y', ['x','y'])
y=(%c-3*(-x-1)*%e^-x)*%e^x
sage: maxima.de_solve('diff(y,x) + 3*x = y', ['x','y'],[1,1])
y=-%e^-1*(5*%e^x-3*%e*x-3*%e)
Solves an ordinary differential equation (ODE) using Laplace transforms.
INPUT:
EXAMPLES:
sage: maxima.clear('x'); maxima.clear('f')
sage: maxima.de_solve_laplace("diff(f(x),x,2) = 2*diff(f(x),x)-f(x)", ["x","f"], [0,1,2])
f(x)=x*%e^x+%e^x
sage: maxima.clear('x'); maxima.clear('f')
sage: f = maxima.de_solve_laplace("diff(f(x),x,2) = 2*diff(f(x),x)-f(x)", ["x","f"])
sage: f
f(x)=x*%e^x*('at('diff(f(x),x,1),x=0))-f(0)*x*%e^x+f(0)*%e^x
sage: print f
!
x d ! x x
f(x) = x %e (-- (f(x))! ) - f(0) x %e + f(0) %e
dx !
!x = 0
Note
The second equation sets the values of 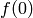 and
and
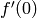 in Maxima, so subsequent ODEs involving these
variables will have these initial conditions automatically
imposed.
in Maxima, so subsequent ODEs involving these
variables will have these initial conditions automatically
imposed.
EXAMPLES:
sage: maxima.demo('array') # not tested
batching /opt/sage/local/share/maxima/5.16.3/demo/array.dem
At the _ prompt, type ‘;’ followed by enter to get next demo subscrmap : true _
EXAMPLES:
sage: maxima.help('gcd')
-- Function: gcd (<p_1>, <p_2>, <x_1>, ...)
...
EXAMPLES:
sage: maxima.example('arrays')
a[n]:=n*a[n-1]
a := n a
n n - 1
a[0]:1
a[5]
120
a[n]:=n
a[6]
6
a[4]
24
done
Return the Maxima function with given arguments and definition.
INPUT:
EXAMPLES:
sage: f = maxima.function('x', 'sin(x)')
sage: f(3.2)
-.05837414342758009
sage: f = maxima.function('x,y', 'sin(x)+cos(y)')
sage: f(2,3.5)
sin(2)-.9364566872907963
sage: f
sin(x)+cos(y)
sage: g = f.integrate('z')
sage: g
(cos(y)+sin(x))*z
sage: g(1,2,3)
3*(cos(2)+sin(1))
The function definition can be a maxima object:
sage: an_expr = maxima('sin(x)*gamma(x)')
sage: t = maxima.function('x', an_expr)
sage: t
gamma(x)*sin(x)
sage: t(2)
sin(2)
sage: float(t(2))
0.90929742682568171
sage: loads(t.dumps())
gamma(x)*sin(x)
Get the string value of the variable var.
EXAMPLES:
sage: maxima.set('xxxxx', '2')
sage: maxima.get('xxxxx')
'2'
EXAMPLES:
sage: maxima.help('gcd')
-- Function: gcd (<p_1>, <p_2>, <x_1>, ...)
...
Send a lisp command to maxima.
Note
The output of this command is very raw - not pretty.
EXAMPLES:
sage: maxima.lisp("(+ 2 17)") # random formatted output
:lisp (+ 2 17)
19
(
Plot a 2d graph using Maxima / gnuplot.
maxima.plot2d(f, ‘[var, min, max]’, options)
INPUT:
EXAMPLES:
sage: maxima.plot2d('sin(x)','[x,-5,5]') # not tested
sage: opts = '[gnuplot_term, ps], [gnuplot_out_file, "sin-plot.eps"]'
sage: maxima.plot2d('sin(x)','[x,-5,5]',opts) # not tested
The eps file is saved in the current directory.
Plots r = [x(t), y(t)] for t = tmin...tmax using gnuplot with options
INPUT:
EXAMPLES:
sage: maxima.plot2d_parametric(["sin(t)","cos(t)"], "t",[-3.1,3.1]) # not tested
sage: opts = '[gnuplot_preamble, "set nokey"], [gnuplot_term, ps], [gnuplot_out_file, "circle-plot.eps"]'
sage: maxima.plot2d_parametric(["sin(t)","cos(t)"], "t", [-3.1,3.1], options=opts) # not tested
The eps file is saved to the current working directory.
Here is another fun plot:
sage: maxima.plot2d_parametric(["sin(5*t)","cos(11*t)"], "t", [0,2*pi()], nticks=400) # not tested
Plot a 3d graph using Maxima / gnuplot.
maxima.plot3d(f, ‘[x, xmin, xmax]’, ‘[y, ymin, ymax]’, ‘[grid, nx, ny]’, options)
INPUT:
EXAMPLES:
sage: maxima.plot3d('1 + x^3 - y^2', '[x,-2,2]', '[y,-2,2]', '[grid,12,12]') # not tested
sage: maxima.plot3d('sin(x)*cos(y)', '[x,-2,2]', '[y,-2,2]', '[grid,30,30]') # not tested
sage: opts = '[gnuplot_term, ps], [gnuplot_out_file, "sin-plot.eps"]'
sage: maxima.plot3d('sin(x+y)', '[x,-5,5]', '[y,-1,1]', opts) # not tested
The eps file is saved in the current working directory.
Plot a 3d parametric graph with r=(x,y,z), x = x(u,v), y = y(u,v), z = z(u,v), for u = umin...umax, v = vmin...vmax using gnuplot with options.
INPUT:
OUTPUT: displays a plot on screen or saves to a file
EXAMPLES:
sage: maxima.plot3d_parametric(["v*sin(u)","v*cos(u)","v"], ["u","v"],[-3.2,3.2],[0,3]) # not tested
sage: opts = '[gnuplot_term, ps], [gnuplot_out_file, "sin-cos-plot.eps"]'
sage: maxima.plot3d_parametric(["v*sin(u)","v*cos(u)","v"], ["u","v"],[-3.2,3.2],[0,3],opts) # not tested
The eps file is saved in the current working directory.
Here is a torus:
sage: _ = maxima.eval("expr_1: cos(y)*(10.0+6*cos(x)); expr_2: sin(y)*(10.0+6*cos(x)); expr_3: -6*sin(x);") # optional
sage: maxima.plot3d_parametric(["expr_1","expr_2","expr_3"], ["x","y"],[0,6],[0,6]) # not tested
Here is a Mobius strip:
sage: x = "cos(u)*(3 + v*cos(u/2))"
sage: y = "sin(u)*(3 + v*cos(u/2))"
sage: z = "v*sin(u/2)"
sage: maxima.plot3d_parametric([x,y,z],["u","v"],[-3.1,3.2],[-1/10,1/10]) # not tested
Plots a curve determined by a sequence of points.
INPUT:
The points are (x1,y1), (x2,y2), etc.
This function requires maxima 5.9.2 or newer.
Note
More that 150 points can sometimes lead to the program hanging. Why?
EXAMPLES:
sage: zeta_ptsx = [ (pari(1/2 + i*I/10).zeta().real()).precision(1) for i in range (70,150)]
sage: zeta_ptsy = [ (pari(1/2 + i*I/10).zeta().imag()).precision(1) for i in range (70,150)]
sage: maxima.plot_list(zeta_ptsx, zeta_ptsy) # not tested
sage: opts='[gnuplot_preamble, "set nokey"], [gnuplot_term, ps], [gnuplot_out_file, "zeta.eps"]'
sage: maxima.plot_list(zeta_ptsx, zeta_ptsy, opts) # not tested
Plots a list of list of points pts_list=[pts1,pts2,...,ptsn], where each ptsi is of the form [[x1,y1],...,[xn,yn]] x’s must be integers and y’s reals options is a string representing maxima plot2d options.
Requires maxima 5.9.2 at least.
Note
More that 150 points can sometimes lead to the program hanging.
EXAMPLES:
sage: xx = [ i/10.0 for i in range (-10,10)]
sage: yy = [ i/10.0 for i in range (-10,10)]
sage: x0 = [ 0 for i in range (-10,10)]
sage: y0 = [ 0 for i in range (-10,10)]
sage: zeta_ptsx1 = [ (pari(1/2+i*I/10).zeta().real()).precision(1) for i in range (10)]
sage: zeta_ptsy1 = [ (pari(1/2+i*I/10).zeta().imag()).precision(1) for i in range (10)]
sage: maxima.plot_multilist([[zeta_ptsx1,zeta_ptsy1],[xx,y0],[x0,yy]]) # not tested
sage: zeta_ptsx1 = [ (pari(1/2+i*I/10).zeta().real()).precision(1) for i in range (10,150)]
sage: zeta_ptsy1 = [ (pari(1/2+i*I/10).zeta().imag()).precision(1) for i in range (10,150)]
sage: maxima.plot_multilist([[zeta_ptsx1,zeta_ptsy1],[xx,y0],[x0,yy]]) # not tested
sage: opts='[gnuplot_preamble, "set nokey"]'
sage: maxima.plot_multilist([[zeta_ptsx1,zeta_ptsy1],[xx,y0],[x0,yy]],opts) # not tested
Set the variable var to the given value.
INPUT:
EXAMPLES:
sage: maxima.set('xxxxx', '2')
sage: maxima.get('xxxxx')
'2'
Wraps maxima’s linsolve.
INPUT: eqns is a list of m strings, each representing a linear question in m = n variables vars is a list of n strings, each representing a variable
EXAMPLES:
sage: eqns = ["x + z = y","2*a*x - y = 2*a^2","y - 2*z = 2"]
sage: vars = ["x","y","z"]
sage: maxima.solve_linear(eqns, vars)
[x=a+1,y=2*a,z=a-1]
Return all Maxima commands, which is useful for tab completion.
EXAMPLES:
sage: t = maxima.trait_names(verbose=False)
sage: 'gcd' in t
True
sage: len(t) # random output
1840
Finds a unit of the ring of integers of the quadratic number field
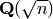 ,
, 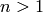 , using the qunit maxima
command.
, using the qunit maxima
command.
EXAMPLES:
sage: u = maxima.unit_quadratic_integer(101); u
a + 10
sage: u.parent()
Number Field in a with defining polynomial x^2 - 101
sage: u = maxima.unit_quadratic_integer(13)
sage: u
5*a + 18
sage: u.parent()
Number Field in a with defining polynomial x^2 - 13
Return the version of Maxima that Sage includes.
EXAMPLES:
sage: maxima.version()
'5.20.1'
Bases: sage.interfaces.expect.ExpectElement
EXAMPLES:
sage: maxima(0).bool()
False
sage: maxima(1).bool()
True
Form the expression that would be written ‘self, args’ in Maxima.
EXAMPLES:
sage: maxima('sqrt(2) + I').comma('numer')
I+1.414213562373095
sage: maxima('sqrt(2) + I*a').comma('a=5')
5*I+sqrt(2)
Return the n-th derivative of self.
INPUT:
OUTPUT: n-th derivative of self with respect to the variable var
EXAMPLES:
sage: f = maxima('x^2')
sage: f.diff()
2*x
sage: f.diff('x')
2*x
sage: f.diff('x', 2)
2
sage: maxima('sin(x^2)').diff('x',4)
16*x^4*sin(x^2)-12*sin(x^2)-48*x^2*cos(x^2)
sage: f = maxima('x^2 + 17*y^2')
sage: f.diff('x')
34*y*'diff(y,x,1)+2*x
sage: f.diff('y')
34*y
Return the n-th derivative of self.
INPUT:
OUTPUT: n-th derivative of self with respect to the variable var
EXAMPLES:
sage: f = maxima('x^2')
sage: f.diff()
2*x
sage: f.diff('x')
2*x
sage: f.diff('x', 2)
2
sage: maxima('sin(x^2)').diff('x',4)
16*x^4*sin(x^2)-12*sin(x^2)-48*x^2*cos(x^2)
sage: f = maxima('x^2 + 17*y^2')
sage: f.diff('x')
34*y*'diff(y,x,1)+2*x
sage: f.diff('y')
34*y
EXAMPLES:
sage: F = maxima('x^5 - y^5').factor()
sage: F.display2d ()
4 3 2 2 3 4
- (y - x) (y + x y + x y + x y + x )
Implements the notation self . other.
EXAMPLES:
sage: A = maxima('matrix ([a1],[a2])')
sage: B = maxima('matrix ([b1, b2])')
sage: A.dot(B)
matrix([a1*b1,a1*b2],[a2*b1,a2*b2])
Return the imaginary part of this maxima element.
EXAMPLES:
sage: maxima('2 + (2/3)*%i').imag()
2/3
Return the integral of self with respect to the variable x.
INPUT:
Returns the definite integral if xmin is not None, otherwise returns an indefinite integral.
EXAMPLES:
sage: maxima('x^2+1').integral()
x^3/3+x
sage: maxima('x^2+ 1 + y^2').integral('y')
y^3/3+x^2*y+y
sage: maxima('x / (x^2+1)').integral()
log(x^2+1)/2
sage: maxima('1/(x^2+1)').integral()
atan(x)
sage: maxima('1/(x^2+1)').integral('x', 0, infinity)
%pi/2
sage: maxima('x/(x^2+1)').integral('x', -1, 1)
0
sage: f = maxima('exp(x^2)').integral('x',0,1); f
-sqrt(%pi)*%i*erf(%i)/2
sage: f.numer()
1.462651745907182
Return the integral of self with respect to the variable x.
INPUT:
Returns the definite integral if xmin is not None, otherwise returns an indefinite integral.
EXAMPLES:
sage: maxima('x^2+1').integral()
x^3/3+x
sage: maxima('x^2+ 1 + y^2').integral('y')
y^3/3+x^2*y+y
sage: maxima('x / (x^2+1)').integral()
log(x^2+1)/2
sage: maxima('1/(x^2+1)').integral()
atan(x)
sage: maxima('1/(x^2+1)').integral('x', 0, infinity)
%pi/2
sage: maxima('x/(x^2+1)').integral('x', -1, 1)
0
sage: f = maxima('exp(x^2)').integral('x',0,1); f
-sqrt(%pi)*%i*erf(%i)/2
sage: f.numer()
1.462651745907182
Return a numerical approximation to the integral of self from a to b.
INPUT:
OUTPUT:
approximation to the integral
estimated absolute error of the approximation
the number of integrand evaluations
an error code:
- 0 - no problems were encountered
- 1 - too many subintervals were done
- 2 - excessive roundoff error
- 3 - extremely bad integrand behavior
- 4 - failed to converge
- 5 - integral is probably divergent or slowly convergent
- 6 - the input is invalid
EXAMPLES:
sage: maxima('exp(-sqrt(x))').nintegral('x',0,1)
(.5284822353142306, 4.163314137883845e-11, 231, 0)
Note that GP also does numerical integration, and can do so to very high precision very quickly:
sage: gp('intnum(x=0,1,exp(-sqrt(x)))')
0.5284822353142307136179049194 # 32-bit
0.52848223531423071361790491935415653021 # 64-bit
sage: _ = gp.set_precision(80)
sage: gp('intnum(x=0,1,exp(-sqrt(x)))')
0.52848223531423071361790491935415653021675547587292866196865279321015401702040079
Return numerical approximation to self as a Maxima object.
EXAMPLES:
sage: a = maxima('sqrt(2)').numer(); a
1.414213562373095
sage: type(a)
<class 'sage.interfaces.maxima.MaximaElement'>
Return the partial fraction decomposition of self with respect to the variable var.
EXAMPLES:
sage: f = maxima('1/((1+x)*(x-1))')
sage: f.partial_fraction_decomposition('x')
1/(2*(x-1))-1/(2*(x+1))
sage: print f.partial_fraction_decomposition('x')
1 1
--------- - ---------
2 (x - 1) 2 (x + 1)
Return the real part of this maxima element.
EXAMPLES:
sage: maxima('2 + (2/3)*%i').real()
2
Return string representation of this maxima object.
EXAMPLES:
sage: maxima('sqrt(2) + 1/3').str()
'sqrt(2)+1/3'
Substitute a value or several values into this Maxima object.
EXAMPLES:
sage: maxima('a^2 + 3*a + b').subst('b=2')
a^2+3*a+2
sage: maxima('a^2 + 3*a + b').subst('a=17')
b+340
sage: maxima('a^2 + 3*a + b').subst('a=17, b=2')
342
Return all Maxima commands, which is useful for tab completion.
EXAMPLES:
sage: m = maxima(2)
sage: 'gcd' in m.trait_names()
True
Bases: sage.interfaces.maxima.MaximaElement
Returns the arguments of this Maxima function.
EXAMPLES:
sage: f = maxima.function('x,y','sin(x+y)')
sage: f.arguments()
['x', 'y']
sage: f.arguments(split=False)
'x,y'
sage: f = maxima.function('', 'sin(x)')
sage: f.arguments()
[]
Returns the definition of this Maxima function as a string.
EXAMPLES:
sage: f = maxima.function('x,y','sin(x+y)')
sage: f.definition()
'sin(x+y)'
Returns the integral of self with respect to the variable var.
Note that integrate is an alias of integral.
EXAMPLES:
sage: x,y = var('x,y')
sage: f = maxima.function('x','sin(x)')
sage: f.integral(x)
-cos(x)
sage: f.integral(y)
sin(x)*y
Returns the integral of self with respect to the variable var.
Note that integrate is an alias of integral.
EXAMPLES:
sage: x,y = var('x,y')
sage: f = maxima.function('x','sin(x)')
sage: f.integral(x)
-cos(x)
sage: f.integral(y)
sin(x)*y
Returns True if x is of type MaximaElement.
EXAMPLES:
sage: from sage.interfaces.maxima import is_MaximaElement
sage: m = maxima(1)
sage: is_MaximaElement(m)
True
sage: is_MaximaElement(1)
False
Spawn a new Maxima command-line session.
EXAMPLES:
sage: from sage.interfaces.maxima import maxima_console
sage: maxima_console() # not tested
Maxima 5.16.3 http://maxima.sourceforge.net
...
EXAMPLES:
sage: from sage.interfaces.maxima import maxima_version
sage: maxima_version()
'5.20.1'
EXAMPLES:
sage: from sage.interfaces.maxima import reduce_load_Maxima
sage: reduce_load_Maxima()
Maxima