Interface to Mathematica

The Mathematica interface will only work if Mathematica is installed on your computer with a command line interface that runs when you give the math command. The interface offers three pieces of functionality:

1. mathematica_console() - A function that dumps you into an interactive command-line Mathematica session. This is an enhanced version of the usual Mathematica command-line, in that it provides readline editing and history (the usual one doesn’t!)
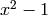2. mathematica(expr) - Creation of a Sage object that wraps a Mathematica object. This provides a Pythonic interface to Mathematica. For example, if f=mathematica('x2-1'), then f.Factor() returns the factorization of computed using Mathematica.
3. mathematica.eval(expr) - Evaluation of arbitrary Mathematica expressions, with the result returned as a string.

Tutorial

We follow some of the tutorial from http://library.wolfram.com/conferences/devconf99/withoff/Basic1.html/.

For any of this to work you must buy and install the Mathematica program, and it must be available as the command math in your PATH.

Syntax

Now make 1 and add it to itself. The result is a Mathematica object.

sage: m = mathematica
sage: a = m(1) + m(1); a                # optional - mathematica
2
sage: a.parent()                        # optional - mathematica
Mathematica
sage: m('1+1')                          # optional - mathematica
2
sage: m(3)**m(50)                       # optional - mathematica
717897987691852588770249

The following is equivalent to Plus[2, 3] in Mathematica:

sage: m = mathematica                          
sage: m(2).Plus(m(3))                   # optional - mathematica
5

We can also compute .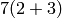

sage: m(7).Times(m(2).Plus(m(3)))       # optional - mathematica
35
sage: m('7(2+3)')                       # optional - mathematica
35

Some typical input

We solve an equation and a system of two equations:

sage: eqn = mathematica('3x + 5 == 14') # optional - mathematica
sage: eqn                               # optional - mathematica
5 + 3*x == 14
sage: eqn.Solve('x')                    # optional - mathematica
{{x -> 3}}
sage: sys = mathematica('{x^2 - 3y == 3, 2x - y == 1}')  # optional - mathematica
sage: print sys                         # optional - mathematica
           2
         {x  - 3 y == 3, 2 x - y == 1}
sage: sys.Solve('{x, y}')               # optional - mathematica
{{y -> -1, x -> 0}, {y -> 11, x -> 6}}

Assignments and definitions

If you assign the mathematica 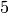to a variable in Sage, this does not affect the in Mathematica.

sage: c = m(5)                          # optional - mathematica
sage: print m('b + c x')                # optional - mathematica
             b + c x
sage: print m('b') + c*m('x')           # optional - mathematica
         b + 5 x

The Sage interfaces changes Sage lists into Mathematica lists:

sage: m = mathematica
sage: eq1 = m('x^2 - 3y == 3')          # optional - mathematica
sage: eq2 = m('2x - y == 1')            # optional - mathematica
sage: v = m([eq1, eq2]); v              # optional - mathematica
{x^2 - 3*y == 3, 2*x - y == 1}
sage: v.Solve(['x', 'y'])               # optional - mathematica
{{y -> -1, x -> 0}, {y -> 11, x -> 6}}

Function definitions

Define mathematica functions by simply sending the definition to the interpreter.

sage: m = mathematica
sage: _ = mathematica('f[p_] = p^2');   # optional - mathematica
sage: m('f[9]')                         # optional - mathematica
81

Numerical Calculations

We find the such that .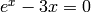

sage: e = mathematica('Exp[x] - 3x == 0') # optional - mathematica
sage: e.FindRoot(['x', 2])                # optional - mathematica
{x -> 1.512134551657842}

Note that this agrees with what the PARI interpreter gp produces:

sage: gp('solve(x=1,2,exp(x)-3*x)')
1.512134551657842473896739678              # 32-bit
1.5121345516578424738967396780720387046    # 64-bit

Next we find the minimum of a polynomial using the two different ways of accessing Mathematica:

sage: mathematica('FindMinimum[x^3 - 6x^2 + 11x - 5, {x,3}]')  # optional - mathematica
{0.6150998205402516, {x -> 2.5773502699629733}}
sage: f = mathematica('x^3 - 6x^2 + 11x - 5')  # optional - mathematica
sage: f.FindMinimum(['x', 3])                  # optional - mathematica
{0.6150998205402516, {x -> 2.5773502699629733}}

Polynomial and Integer Factorization

We factor a polynomial of degree 200 over the integers.

sage: R.<x> = PolynomialRing(ZZ)
sage: f = (x**100+17*x+5)*(x**100-5*x+20)
sage: f
x^200 + 12*x^101 + 25*x^100 - 85*x^2 + 315*x + 100
sage: g = mathematica(str(f))            # optional - mathematica
sage: print g                            # optional - mathematica
                           2       100       101    200
         100 + 315 x - 85 x  + 25 x    + 12 x    + x
sage: g                                  # optional - mathematica
100 + 315*x - 85*x^2 + 25*x^100 + 12*x^101 + x^200
sage: print g.Factor()                   # optional - mathematica
                      100               100
         (20 - 5 x + x   ) (5 + 17 x + x   )

We can also factor a multivariate polynomial:

sage: f = mathematica('x^6 + (-y - 2)*x^5 + (y^3 + 2*y)*x^4 - y^4*x^3')  # optional - mathematica
sage: print f.Factor()                   # optional - mathematica
          3                  2    3
         x  (x - y) (-2 x + x  + y )

We factor an integer:

sage: n = mathematica(2434500)           # optional - mathematica
sage: n.FactorInteger()                  # optional - mathematica
{{2, 2}, {3, 2}, {5, 3}, {541, 1}}
sage: n = mathematica(2434500)           # optional - mathematica
sage: F = n.FactorInteger(); F           # optional - mathematica
{{2, 2}, {3, 2}, {5, 3}, {541, 1}}
sage: F[1]                               # optional - mathematica
{2, 2}
sage: F[4]                               # optional - mathematica
{541, 1}

We can also load the ECM package and factoring using it:

sage: _ = mathematica.eval("<<NumberTheory`FactorIntegerECM`");  # optional - mathematica
sage: mathematica.FactorIntegerECM('932901*939321')              # optional - mathematica
8396109

Long Input

The Mathematica interface reads in even very long input (using files) in a robust manner.

sage: t = '"%s"'%10^10000   # ten thousand character string.
sage: a = mathematica(t)        # optional - mathematica
sage: a = mathematica.eval(t)   # optional - mathematica

Loading and saving

Mathematica has an excellent InputForm function, which makes saving and loading Mathematica objects possible. The first examples test saving and loading to strings.

sage: x = mathematica(pi/2)     # optional - mathematica
sage: print x                   # optional - mathematica
         Pi
         --
         2
sage: loads(dumps(x)) == x      # optional - mathematica
True
sage: n = x.N(50)               # optional - mathematica
sage: print n                   # optional - mathematica
              1.5707963267948966192313216916397514420985846996876
sage: loads(dumps(n)) == n      # optional - mathematica
True

OTHER Examples:

sage: def math_bessel_K(nu,x):
...       return mathematica(nu).BesselK(x).N(20).sage()
...
sage: math_bessel_K(2,I)                      # optional - mathematica
0.180489972066962*I - 2.592886175491197         # 32-bit
-2.592886175491196978 + 0.1804899720669620266*I # 64-bit

sage: slist = [[1, 2], 3., 4 + I]
sage: mlist = mathematica(slist); mlist     # optional - mathematica
{{1, 2}, 3., 4 + I}
sage: slist2 = list(mlist); slist2          # optional - mathematica
[{1, 2}, 3., 4 + I]  
sage: slist2[0]                             # optional - mathematica
{1, 2}
sage: slist2[0].parent()                    # optional - mathematica
Mathematica
sage: slist3 = mlist.sage(); slist3         # optional - mathematica
[[1, 2], 3.00000000000000, I + 4]

sage: mathematica('10.^80')     # optional - mathematica
1.*^80
sage: mathematica('10.^80').sage()  # optional - mathematica
1.00000000000000e80

AUTHORS:

• William Stein (2005): first version
• Doug Cutrell (2006-03-01): Instructions for use under Cygwin/Windows.
• Felix Lawrence (2009-08-21): Added support for importing Mathematica lists and floats with exponents.

class sage.interfaces.mathematica.Mathematica(maxread=100, script_subdirectory='', logfile=None, server=None, server_tmpdir=None)

Bases: sage.interfaces.expect.Expect

Interface to the Mathematica interpreter.

chdir(dir)

Change Mathematica’s current working directory.

EXAMPLES:

sage: mathematica.chdir('/')          # optional
sage: mathematica('Directory[]')      # optional
"/"

console(readline=True)

eval(code, strip=True, **kwds)

get(var, ascii_art=False)

Get the value of the variable var.

AUTHORS:

• William Stein
• Kiran Kedlaya (2006-02-04): suggested using InputForm

help(cmd)

set(var, value)

Set the variable var to the given value.

trait_names()

class sage.interfaces.mathematica.MathematicaElement(parent, value, is_name=False, name=None)

Bases: sage.interfaces.expect.ExpectElement

show(filename=None, ImageSize=600)

Show a mathematica expression or plot in the Sage notebook.

EXAMPLES:

sage: P = mathematica('Plot[Sin[x],{x,-2Pi,4Pi}]')   # optional - mathematica
sage: show(P)                                        # optional - mathematica
sage: P.show(ImageSize=800)                          # optional - mathematica
sage: Q = mathematica('Sin[x Cos[y]]/Sqrt[1-x^2]')   # optional - mathematica
sage: show(Q)                                        # optional - mathematica
<html><div class="math">\frac{\sin (x \cos (y))}{\sqrt{1-x^2}}</div></html>

str()

class sage.interfaces.mathematica.MathematicaFunction(parent, name)

Bases: sage.interfaces.expect.ExpectFunction

class sage.interfaces.mathematica.MathematicaFunctionElement(obj, name)

Bases: sage.interfaces.expect.FunctionElement

sage.interfaces.mathematica.clean_output(s)

sage.interfaces.mathematica.mathematica_console(readline=True)

sage.interfaces.mathematica.reduce_load(X)