AUTHORS:
ACKNOWLEDGMENT: (From Liu’s website:) Many thanks to Henri Cohen who started writing this program. After this program is available, many people pointed out to me (mathematical as well as programming) bugs : B. Poonen, E. Schaefer, C. Stahlke, M. Stoll, F. Villegas. So thanks to all of them. Thanks also go to Ph. Depouilly who help me to compile the program.
Also Liu has given me explicit permission to include genus2reduction with Sage and for people to modify the C source code however they want.
Bases: sage.structure.sage_object.SageObject
Conductor and Reduction Types for Genus 2 Curves.
Use R = genus2reduction(Q, P) to obtain reduction
information about the Jacobian of the projective smooth curve
defined by  . Type R?
for further documentation and a description of how to interpret the
local reduction data.
. Type R?
for further documentation and a description of how to interpret the
local reduction data.
EXAMPLES:
sage: x = QQ['x'].0
sage: R = genus2reduction(x^3 - 2*x^2 - 2*x + 1, -5*x^5)
sage: R.conductor
1416875
sage: factor(R.conductor)
5^4 * 2267
This means that only the odd part of the conductor is known.
sage: R.prime_to_2_conductor_only
True
The discriminant is always minimal away from 2, but possibly not at 2.
sage: factor(R.minimal_disc)
2^3 * 5^5 * 2267
Printing R summarizes all the information computed about the curve
sage: R
Reduction data about this proper smooth genus 2 curve:
y^2 + (x^3 - 2*x^2 - 2*x + 1)*y = -5*x^5
A Minimal Equation (away from 2):
y^2 = x^6 - 240*x^4 - 2550*x^3 - 11400*x^2 - 24100*x - 19855
Minimal Discriminant (away from 2): 56675000
Conductor (away from 2): 1416875
Local Data:
p=2
(potential) stable reduction: (II), j=1
p=5
(potential) stable reduction: (I)
reduction at p: [V] page 156, (3), f=4
p=2267
(potential) stable reduction: (II), j=432
reduction at p: [I{1-0-0}] page 170, (1), f=1
Here are some examples of curves with modular Jacobians:
sage: R = genus2reduction(x^3 + x + 1, -2*x^5 - 3*x^2 + 2*x - 2)
sage: factor(R.conductor)
23^2
sage: factor(genus2reduction(x^3 + 1, -x^5 - 3*x^4 + 2*x^2 + 2*x - 2).conductor)
29^2
sage: factor(genus2reduction(x^3 + x + 1, x^5 + 2*x^4 + 2*x^3 + x^2 - x - 1).conductor)
5^6
EXAMPLE:
sage: genus2reduction(0, x^6 + 3*x^3 + 63)
Reduction data about this proper smooth genus 2 curve:
y^2 = x^6 + 3*x^3 + 63
A Minimal Equation (away from 2):
y^2 = x^6 + 3*x^3 + 63
Minimal Discriminant (away from 2): 10628388316852992
Conductor (away from 2): 2893401
Local Data:
p=2
(potential) stable reduction: (V), j1+j2=0, j1*j2=0
p=3
(potential) stable reduction: (I)
reduction at p: [III{9}] page 184, (3)^2, f=10
p=7
(potential) stable reduction: (V), j1+j2=0, j1*j2=0
reduction at p: [I{0}-II-0] page 159, (1), f=2
In the above example, Liu remarks that in fact at 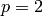 ,
the reduction is [II-II-0] page 163, (1),
,
the reduction is [II-II-0] page 163, (1), 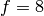 . So the
conductor of J(C) is actually
. So the
conductor of J(C) is actually 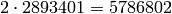 .
.
A MODULAR CURVE:
Consider the modular curve 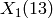 defined by an
equation
defined by an
equation
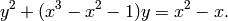
We have:
sage: genus2reduction(x^3-x^2-1, x^2 - x)
Reduction data about this proper smooth genus 2 curve:
y^2 + (x^3 - x^2 - 1)*y = x^2 - x
A Minimal Equation (away from 2):
y^2 = x^6 + 58*x^5 + 1401*x^4 + 18038*x^3 + 130546*x^2 + 503516*x + 808561
Minimal Discriminant (away from 2): 169
Conductor: 169
Local Data:
p=13
(potential) stable reduction: (V), j1+j2=0, j1*j2=0
reduction at p: [I{0}-II-0] page 159, (1), f=2
So the curve has good reduction at 2. At 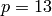 , the stable
reduction is union of two elliptic curves, and both of them have 0
as modular invariant. The reduction at 13 is of type [I_0-II-0]
(see Namikawa-Ueno, page 159). It is an elliptic curve with a cusp.
The group of connected components of the Neron model of
, the stable
reduction is union of two elliptic curves, and both of them have 0
as modular invariant. The reduction at 13 is of type [I_0-II-0]
(see Namikawa-Ueno, page 159). It is an elliptic curve with a cusp.
The group of connected components of the Neron model of
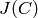 is trivial, and the exponent of the conductor of
is trivial, and the exponent of the conductor of
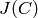 at
at 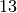 is
is 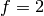 . The conductor of
. The conductor of
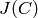 is
is 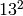 . (Note: It is a theorem of
Conrad-Edixhoven-Stein that the component group of
. (Note: It is a theorem of
Conrad-Edixhoven-Stein that the component group of
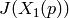 is trivial for all primes
is trivial for all primes  .)
.)
Return the raw output of running the
genus2reduction program on the hyperelliptic curve
 as a string.
as a string.
INPUT:
OUTPUT:
EXAMPLES:
sage: x = QQ['x'].0
sage: print genus2reduction.raw(x^3 - 2*x^2 - 2*x + 1, -5*x^5)[0]
a minimal equation over Z[1/2] is :
y^2 = x^6-240*x^4-2550*x^3-11400*x^2-24100*x-19855
<BLANKLINE>
factorization of the minimal (away from 2) discriminant :
[2,3;5,5;2267,1]
<BLANKLINE>
p=2
(potential) stable reduction : (II), j=1
p=5
(potential) stable reduction : (I)
reduction at p : [V] page 156, (3), f=4
p=2267
(potential) stable reduction : (II), j=432
reduction at p : [I{1-0-0}] page 170, (1), f=1
<BLANKLINE>
the prime to 2 part of the conductor is 1416875
in factorized form : [2,0;5,4;2267,1]
Verify that we fix trac 5573:
sage: genus2reduction(x^3 + x^2 + x,-2*x^5 + 3*x^4 - x^3 - x^2 - 6*x - 2)
Reduction data about this proper smooth genus 2 curve:
y^2 + (x^3 + x^2 + x)*y = -2*x^5 + 3*x^4 - x^3 - x^2 - 6*x - 2
...
Bases: sage.structure.sage_object.SageObject
Reduction data for a genus 2 curve.
How to read local_data attribute, i.e., if this class is R, then the following is the meaning of R.local_data[p].
For each prime number  dividing the discriminant of
dividing the discriminant of
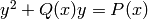 , there are two lines.
, there are two lines.
The first line contains information about the stable reduction after field extension. Here are the meanings of the symbols of stable reduction :
(I) The stable reduction is smooth (i.e. the curve has potentially good reduction).
(II) The stable reduction is an elliptic curve  with an
ordinary double point.
with an
ordinary double point. 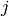 mod
mod  is the modular
invariant of
is the modular
invariant of  .
.
(III) The stable reduction is a projective line with two ordinary double points.
(IV) The stable reduction is two projective lines crossing transversally at three points.
(V) The stable reduction is the union of two elliptic curves
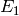 and
and 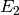 intersecting transversally at one
point. Let
intersecting transversally at one
point. Let 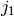 ,
, 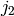 be their modular
invariants, then
be their modular
invariants, then 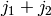 and
and 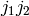 are
computed (they are numbers mod
are
computed (they are numbers mod  ).
).
(VI) The stable reduction is the union of an elliptic curve
 and a projective line which has an ordinary double
point. These two components intersect transversally at one point.
and a projective line which has an ordinary double
point. These two components intersect transversally at one point.
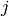 mod
mod  is the modular invariant of
is the modular invariant of
 .
.
(VII) The stable reduction is as above, but the two components are both singular.
In the cases (I) and (V), the Jacobian 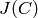 has
potentially good reduction. In the cases (III), (IV) and (VII),
has
potentially good reduction. In the cases (III), (IV) and (VII),
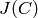 has potentially multiplicative reduction. In the two
remaining cases, the (potential) semi-abelian reduction of
has potentially multiplicative reduction. In the two
remaining cases, the (potential) semi-abelian reduction of
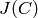 is extension of an elliptic curve (with modular
invariant
is extension of an elliptic curve (with modular
invariant 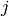 mod
mod  ) by a torus.
) by a torus.
The second line contains three data concerning the reduction at
 without any field extension.
without any field extension.
The first symbol describes the REDUCTION AT  of
of
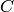 . We use the symbols of Namikawa-Ueno for the type of
the reduction (Namikawa, Ueno:”The complete classification of
fibers in pencils of curves of genus two”, Manuscripta Math., vol.
9, (1973), pages 143-186.) The reduction symbol is followed by the
corresponding page number (or just an indiction) in the above
article. The lower index is printed by , for instance, [I2-II-5]
means [I_2-II-5]. Note that if
. We use the symbols of Namikawa-Ueno for the type of
the reduction (Namikawa, Ueno:”The complete classification of
fibers in pencils of curves of genus two”, Manuscripta Math., vol.
9, (1973), pages 143-186.) The reduction symbol is followed by the
corresponding page number (or just an indiction) in the above
article. The lower index is printed by , for instance, [I2-II-5]
means [I_2-II-5]. Note that if  and
and  are
Kodaira symbols for singular fibers of elliptic curves, [K-K’-m]
and [K’-K-m] are the same type. Finally, [K-K’-1] (not the same as
[K-K’-1]) is [K’-K-alpha] in the notation of Namikawa-Ueno. The
figure [2I_0-m] in Namikawa-Ueno, page 159 must be denoted by
[2I_0-(m+1)].
are
Kodaira symbols for singular fibers of elliptic curves, [K-K’-m]
and [K’-K-m] are the same type. Finally, [K-K’-1] (not the same as
[K-K’-1]) is [K’-K-alpha] in the notation of Namikawa-Ueno. The
figure [2I_0-m] in Namikawa-Ueno, page 159 must be denoted by
[2I_0-(m+1)].
The second datum is the GROUP OF CONNECTED COMPONENTS (over an
ALGEBRAIC CLOSURE (!) of 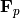 ) of the Neron
model of J(C). The symbol (n) means the cyclic group with n
elements. When n=0, (0) is the trivial group (1).
Hn is isomorphic to (2)x(2) if n is even and to (4)
otherwise.
) of the Neron
model of J(C). The symbol (n) means the cyclic group with n
elements. When n=0, (0) is the trivial group (1).
Hn is isomorphic to (2)x(2) if n is even and to (4)
otherwise.
Note - The set of rational points of 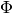 can be computed
using Theorem 1.17 in S. Bosch and Q. Liu “Rational points of the
group of components of a Neron model”, Manuscripta Math. 98 (1999),
275-293.
can be computed
using Theorem 1.17 in S. Bosch and Q. Liu “Rational points of the
group of components of a Neron model”, Manuscripta Math. 98 (1999),
275-293.
Finally, 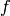 is the exponent of the conductor of
is the exponent of the conductor of
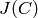 at
at  .
.
Warning
Be careful regarding the formula:

(Q. Liu : “Conducteur et discriminant minimal de courbes de genre
2”, Compositio Math. 94 (1994) 51-79, Theoreme 2) is valid only if
the residual field is algebraically closed as stated in the paper.
So this equality does not hold in general over
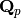 . The fact is that the minimal discriminant
may change after unramified extension. One can show however that,
at worst, the change will stabilize after a quadratic unramified
extension (Q. Liu : “Modeles entiers de courbes hyperelliptiques
sur un corps de valuation discrete”, Trans. AMS 348 (1996),
4577-4610, Section 7.2, Proposition 4).
. The fact is that the minimal discriminant
may change after unramified extension. One can show however that,
at worst, the change will stabilize after a quadratic unramified
extension (Q. Liu : “Modeles entiers de courbes hyperelliptiques
sur un corps de valuation discrete”, Trans. AMS 348 (1996),
4577-4610, Section 7.2, Proposition 4).