CHomP stands for “Computation Homology Program”, and is good at computing homology of simplicial complexes, cubical complexes, and chain complexes. It can also compute homomorphisms induced on homology by maps. See the CHomP web page http://chomp.rutgers.edu/ for more information.
AUTHOR:
Interface to the CHomP package.
| Parameters: |
|
|---|---|
| Returns: | homology groups as a dictionary indexed by dimension |
The programs homsimpl, homcubes, and homchain are available through this interface. homsimpl computes the relative or absolute homology groups of simplicial complexes. homcubes computes the relative or absolute homology groups of cubical complexes. homchain computes the homology groups of chain complexes. For consistency with Sage’s other homology computations, the answers produced by homsimpl and homcubes in the absolute case are converted to reduced homology.
Note also that CHomP can only compute over the integers or
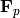 . CHomP is fast enough, though, that if you want
rational information, you should consider using CHomP with integer
coefficients, or with mod
. CHomP is fast enough, though, that if you want
rational information, you should consider using CHomP with integer
coefficients, or with mod  coefficients for a sufficiently
large
coefficients for a sufficiently
large  , rather than using Sage’s built-in homology algorithms.
, rather than using Sage’s built-in homology algorithms.
See also the documentation for the functions homchain(), homcubes(), and homsimpl() for more examples, including illustrations of some of the optional parameters.
EXAMPLES:
sage: from sage.interfaces.chomp import CHomP
sage: T = cubical_complexes.Torus()
sage: CHomP()('homcubes', T) # optional: need CHomP
{0: 0, 1: Z x Z, 2: Z}
Relative homology of a segment relative to its endpoints:
sage: edge = simplicial_complexes.Simplex(1)
sage: ends = edge.n_skeleton(0)
sage: CHomP()('homsimpl', edge) # optional: need CHomP
{0: 0}
sage: CHomP()('homsimpl', edge, ends) # optional: need CHomP
{0: 0, 1: Z}
Homology of a chain complex:
sage: C = ChainComplex({3: 2 * identity_matrix(ZZ, 2)}, degree=-1)
sage: CHomP()('homchain', C) # optional: need CHomP
{2: C2 x C2}
Print a help message for program, a program from the CHomP suite.
| Parameter: | program (string) – which CHomP program to use |
|---|---|
| Returns: | nothing – just print a message |
EXAMPLES:
sage: from sage.interfaces.chomp import CHomP
sage: CHomP().help('homcubes') # optional: need CHomP
HOMCUBES, ver. ... Copyright (C) ... by Pawel Pilarczyk...
Return True if this computer has program installed.
The first time it is run, this function caches its result in the variable _have_chomp – a dictionary indexed by program name – and any subsequent time, it just checks the value of the variable.
This program is used in the routine CHomP.__call__.
If this computer doesn’t have CHomP installed, you may obtain it from http://chomp.rutgers.edu/.
EXAMPLES:
sage: from sage.interfaces.chomp import have_chomp
sage: have_chomp() # random -- depends on whether CHomP is installed
True
sage: 'homsimpl' in sage.interfaces.chomp._have_chomp
True
sage: sage.interfaces.chomp._have_chomp['homsimpl'] == have_chomp()
True
Compute the homology of a chain complex using the CHomP program homchain.
| Parameters: |
|
|---|---|
| Returns: | homology groups as a dictionary indexed by dimension |
EXAMPLES:
sage: from sage.interfaces.chomp import homchain
sage: C = cubical_complexes.Sphere(3).chain_complex()
sage: homchain(C)[3] # optional: need CHomP
Z
Generators: these are given as a list after the homology group. Each generator is specified as a cycle, an element in the appropriate free module over the base ring:
sage: C2 = delta_complexes.Sphere(2).chain_complex()
sage: homchain(C2, generators=True)[2] # optional: need CHomP
(Z, [(1, -1)])
sage: homchain(C2, generators=True, base_ring=GF(2))[2] # optional: need CHomP
(Vector space of dimension 1 over Finite Field of size 2, [(1, 1)])
TESTS:
Chain complexes concentrated in negative dimensions, cochain complexes, etc.:
sage: C = ChainComplex({-5: 4 * identity_matrix(ZZ, 2)}, degree=-1)
sage: homchain(C) # optional: need CHomP
{-6: C4 x C4}
sage: C = ChainComplex({-5: 4 * identity_matrix(ZZ, 2)}, degree=1)
sage: homchain(C, generators=True) # optional: need CHomP
{-4: (C4 x C4, [(1, 0), (0, 1)])}
Compute the homology of a cubical complex using the CHomP program homcubes. If the argument subcomplex is present, compute homology of complex relative to subcomplex.
| Parameters: |
|
|---|---|
| Returns: | homology groups as a dictionary indexed by dimension |
EXAMPLES:
sage: from sage.interfaces.chomp import homcubes
sage: S = cubical_complexes.Sphere(3)
sage: homcubes(S)[3] # optional: need CHomP
Z
Relative homology:
sage: C3 = cubical_complexes.Cube(3)
sage: bdry = C3.n_skeleton(2)
sage: homcubes(C3, bdry) # optional: need CHomP
{0: 0, 1: 0, 2: 0, 3: Z}
Generators: these are given as a list after the homology group. Each generator is specified as a linear combination of cubes:
sage: print homcubes(cubical_complexes.Sphere(1), generators=True)[1][1] # optional: need CHomP
[[[1,1] x [0,1]] - [[0,1] x [1,1]] + [[0,1] x [0,0]] - [[0,0] x [0,1]]]
Compute the homology of a simplicial complex using the CHomP program homsimpl. If the argument subcomplex is present, compute homology of complex relative to subcomplex.
| Parameters: |
|
|---|---|
| Returns: | homology groups as a dictionary indexed by dimension |
EXAMPLES:
sage: from sage.interfaces.chomp import homsimpl
sage: T = simplicial_complexes.Torus()
sage: M8 = simplicial_complexes.MooreSpace(8)
sage: M4 = simplicial_complexes.MooreSpace(4)
sage: X = T.disjoint_union(T).disjoint_union(T).disjoint_union(M8).disjoint_union(M4)
sage: homsimpl(X)[1] # optional: need CHomP
Z^6 x C4 x C8
Relative homology:
sage: S = simplicial_complexes.Simplex(3)
sage: bdry = S.n_skeleton(2)
sage: homsimpl(S, bdry)[3] # optional: need CHomP
Z
Generators: these are given as a list after the homology group. Each generator is specified as a linear combination of simplices:
sage: homsimpl(S, bdry, generators=True)[3] # optional: need CHomP
(Z, [(0, 1, 2, 3)])
sage: homsimpl(simplicial_complexes.Sphere(1), generators=True) # optional: need CHomP
{0: 0, 1: (Z, [(0, 1) - (0, 2) + (1, 2)])}
TESTS:
Generators for a simplicial complex whose vertices are not integers:
sage: S1 = simplicial_complexes.Sphere(1)
sage: homsimpl(S1.join(S1), generators=True)[3][1] # optional: need CHomP
[-('L0', 'L1', 'R0', 'R1') + ('L0', 'L1', 'R0', 'R2') - ('L0', 'L1', 'R1', 'R2') + ('L0', 'L2', 'R0', 'R1') - ('L0', 'L2', 'R0', 'R2') + ('L0', 'L2', 'R1', 'R2') - ('L1', 'L2', 'R0', 'R1') + ('L1', 'L2', 'R0', 'R2') - ('L1', 'L2', 'R1', 'R2')]
Process CHomP generator information for simplicial complexes.
| Parameters: |
|
|---|---|
| Returns: | list of generators in each dimension, as described below |
gen_string has the form
[H_0]
a1
[H_1]
a2
a3
[H_2]
a1 - a2
For each homology group, each line lists a homology generator as a
linear combination of generators ai of the group of chains in
the appropriate dimension. The elements ai are indexed
starting with 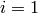 . Each generator is converted, using regular
expressions, from a string to a vector (an element in the free
module over base_ring), with ai representing the unit
vector in coordinate
. Each generator is converted, using regular
expressions, from a string to a vector (an element in the free
module over base_ring), with ai representing the unit
vector in coordinate 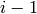 . For example, the string a1 - a2
gets converted to the vector (1, -1).
. For example, the string a1 - a2
gets converted to the vector (1, -1).
Therefore the return value is a list of vectors.
EXAMPLES:
sage: from sage.interfaces.chomp import process_generators_chain
sage: s = "[H_0]\na1\n\n[H_1]\na2\na3\n"
sage: process_generators_chain(s, 1)
[(0, 1), (0, 0, 1)]
sage: s = "[H_0]\na1\n\n[H_1]\n5 * a2 - a1\na3\n"
sage: process_generators_chain(s, 1, base_ring=ZZ)
[(-1, 5), (0, 0, 1)]
sage: process_generators_chain(s, 1, base_ring=GF(2))
[(1, 1), (0, 0, 1)]
Process CHomP generator information for cubical complexes.
| Parameters: |
|
|---|---|
| Returns: | list of generators in each dimension, as described below |
gen_string has the form
The 2 generators of H_1 follow:
generator 1
-1 * [(0,0,0,0,0)(0,0,0,0,1)]
1 * [(0,0,0,0,0)(0,0,1,0,0)]
...
generator 2
-1 * [(0,1,0,1,1)(1,1,0,1,1)]
-1 * [(0,1,0,0,1)(0,1,0,1,1)]
...
Each line consists of a coefficient multiplied by a cube; the cube is specified by its “bottom left” and “upper right” corners.
For technical reasons, we remove the first coordinate of each tuple, and using regular expressions, the remaining parts get converted from a string to a pair (coefficient, Cube), with the cube represented as a product of tuples. For example, the first line in “generator 1” gets turned into
(-1, [0,0] x [0,0] x [0,0] x [0,1])
representing an element in the free abelian group with basis given by cubes. Each generator is a list of such pairs, representing the sum of such elements. These are reassembled in CHomP.__call__() to actual elements in the free module generated by the cubes of the cubical complex in the appropriate dimension.
Therefore the return value is a list of lists of pairs, one list of pairs for each generator.
EXAMPLES:
sage: from sage.interfaces.chomp import process_generators_cubical
sage: s = "The 2 generators of H_1 follow:\ngenerator 1:\n-1 * [(0,0,0,0,0)(0,0,0,0,1)]\n1 * [(0,0,0,0,0)(0,0,1,0,0)]"
sage: process_generators_cubical(s, 1)
[[(-1, [0,0] x [0,0] x [0,0] x [0,1]), (1, [0,0] x [0,1] x [0,0] x [0,0])]]
sage: len(process_generators_cubical(s, 1)) # only one generator
1
Process CHomP generator information for simplicial complexes.
| Parameters: |
|
|---|---|
| Returns: | list of generators in each dimension, as described below |
gen_string has the form
The 2 generators of H_1 follow:
generator 1
-1 * (1,6)
1 * (1,4)
...
generator 2
-1 * (1,6)
1 * (1,4)
...
where each line contains a coefficient and a simplex. Each line is converted, using regular expressions, from a string to a pair (coefficient, Simplex), like
(-1, (1,6))
representing an element in the free abelian group with basis given by simplices. Each generator is a list of such pairs, representing the sum of such elements. These are reassembled in CHomP.__call__() to actual elements in the free module generated by the simplices of the simplicial complex in the appropriate dimension.
Therefore the return value is a list of lists of pairs, one list of pairs for each generator.
EXAMPLES:
sage: from sage.interfaces.chomp import process_generators_simplicial
sage: s = "The 2 generators of H_1 follow:\ngenerator 1:\n-1 * (1,6)\n1 * (1,4)"
sage: process_generators_simplicial(s, 1, simplicial_complexes.Torus())
[[(-1, (1, 6)), (1, (1, 4))]]