AUTHORS:
This module implements the basic structure of finite simplicial
complexes. Given a set 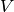 of “vertices”, a simplicial complex on
of “vertices”, a simplicial complex on 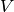 is a collection
is a collection  of subsets of
of subsets of 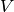 satisfying the condition that if
satisfying the condition that if
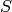 is one of the subsets in
is one of the subsets in  , then so is every subset of
, then so is every subset of 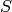 . The
subsets
. The
subsets 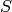 are called the ‘simplices’ of
are called the ‘simplices’ of  .
.
A simplicial complex  can be viewed as a purely combinatorial
object, as described above, but it also gives rise to a topological
space
can be viewed as a purely combinatorial
object, as described above, but it also gives rise to a topological
space 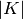 (its geometric realization) as follows: first, the
points of
(its geometric realization) as follows: first, the
points of 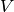 should be in general position in euclidean space. Next,
if
should be in general position in euclidean space. Next,
if 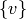 is in
is in  , then the vertex
, then the vertex  is in
is in 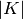 . If
. If 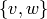 is in
is in  , then the line segment from
, then the line segment from  to
to 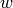 is in
is in 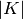 . If
. If  is in
is in  , then the triangle with vertices
, then the triangle with vertices 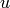 ,
,  , and
, and 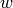 is in
is in 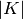 . In general,
. In general, 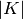 is the union of the convex hulls of
simplices of
is the union of the convex hulls of
simplices of  . Frequently, one abuses notation and uses
. Frequently, one abuses notation and uses  to
denote both the simplicial complex and the associated topological
space.
to
denote both the simplicial complex and the associated topological
space.

For any simplicial complex  and any commutative ring
and any commutative ring 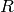 there is
an associated chain complex, with differential of degree
there is
an associated chain complex, with differential of degree  . The
. The
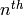 term is the free
term is the free 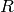 -module with basis given by the
-module with basis given by the
 -simplices of
-simplices of  . The differential is determined by its value on
any simplex: on the
. The differential is determined by its value on
any simplex: on the  -simplex with vertices
-simplex with vertices 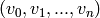 ,
the differential is the alternating sum with
,
the differential is the alternating sum with 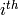 summand
summand  multiplied by the
multiplied by the 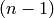 -simplex obtained by omitting vertex
-simplex obtained by omitting vertex 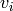 .
.
In the implementation here, the vertex set must be finite. To define a
simplicial complex, specify its vertex set: this should be a list,
tuple, or set, or it can be a non-negative integer  , in which case
the vertex set is
, in which case
the vertex set is 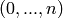 . Also specify the facets: the maximal
faces.
. Also specify the facets: the maximal
faces.
Note
The elements of the vertex set are not automatically contained in the simplicial complex: each one is only included if and only if it is a vertex of at least one of the specified facets.
Note
This class derives from GenericCellComplex, and so inherits its methods. Some of those methods are not listed here; see the Generic Cell Complex page instead.
EXAMPLES:
sage: SimplicialComplex([1, 3, 7], [[1], [3, 7]])
Simplicial complex with vertex set (1, 3, 7) and facets {(3, 7), (1,)}
sage: SimplicialComplex(2) # the empty simplicial complex
Simplicial complex with vertex set (0, 1, 2) and facets {()}
sage: X = SimplicialComplex(3, [[0,1], [1,2], [2,3], [3,0]])
sage: X
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(1, 2), (2, 3), (0, 3), (0, 1)}
sage: X.stanley_reisner_ring()
Quotient of Multivariate Polynomial Ring in x0, x1, x2, x3 over Integer Ring by the ideal (x1*x3, x0*x2)
sage: X.is_pure()
True
Sage can perform a number of operations on simplicial complexes, such as the join and the product, and it can also compute homology:
sage: S = SimplicialComplex(2, [[0,1], [1,2], [0,2]]) # circle
sage: T = S.product(S) # torus
sage: T
Simplicial complex with 9 vertices and 18 facets
sage: T.homology() # this computes reduced homology
{0: 0, 1: Z x Z, 2: Z}
sage: T.euler_characteristic()
0
Sage knows about some basic combinatorial data associated to a simplicial complex:
sage: X = SimplicialComplex(3, [[0,1], [1,2], [2,3], [0,3]])
sage: X.f_vector()
[1, 4, 4]
sage: X.face_poset()
Finite poset containing 8 elements
sage: X.stanley_reisner_ring()
Quotient of Multivariate Polynomial Ring in x0, x1, x2, x3 over Integer Ring by the ideal (x1*x3, x0*x2)
Bases: sage.structure.sage_object.SageObject
Define a simplex.
Topologically, a simplex is the convex hull of a collection of vertices in general position. Combinatorially, it is defined just by specifying a set of vertices. It is represented in Sage by the tuple of the vertices.
| Parameter: | X (integer or list, tuple, or other iterable) – set of vertices |
|---|---|
| Returns: | simplex with those vertices |
X may be a non-negative integer  , in which case the
simplicial complex will have
, in which case the
simplicial complex will have 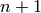 vertices
vertices 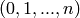 , or
it may be anything which may be converted to a tuple, in which
case the vertices will be that tuple. In the second case, each
vertex must be hashable, so it should be a number, a string, or a
tuple, for instance, but not a list.
, or
it may be anything which may be converted to a tuple, in which
case the vertices will be that tuple. In the second case, each
vertex must be hashable, so it should be a number, a string, or a
tuple, for instance, but not a list.
Warning
The vertices should be distinct, and no error checking is done to make sure this is the case.
EXAMPLES:
sage: Simplex(4)
(0, 1, 2, 3, 4)
sage: Simplex([3, 4, 1])
(3, 4, 1)
sage: X = Simplex((3, 'a', 'vertex')); X
(3, 'a', 'vertex')
sage: X == loads(dumps(X))
True
Vertices may be tuples but not lists:
sage: Simplex([(1,2), (3,4)])
((1, 2), (3, 4))
sage: Simplex([[1,2], [3,4]])
...
TypeError: unhashable type: 'list'
The dimension of this simplex: the number of vertices minus 1.
EXAMPLES:
sage: Simplex(5).dimension() == 5
True
sage: Simplex(5).face(1).dimension()
4
The nth face of this simplex.
| Parameter: | n (integer) – an integer between 0 and the dimension of this simplex |
|---|---|
| Returns: | the simplex obtained by removing the nth vertex from this simplex |
EXAMPLES:
sage: S = Simplex(4)
sage: S.face(0)
(1, 2, 3, 4)
sage: S.face(3)
(0, 1, 2, 4)
The list of faces (of codimension 1) of this simplex.
EXAMPLES:
sage: S = Simplex(4)
sage: S.faces()
[(1, 2, 3, 4), (0, 2, 3, 4), (0, 1, 3, 4), (0, 1, 2, 4), (0, 1, 2, 3)]
sage: len(Simplex(10).faces())
11
Return True iff this simplex is the empty simplex.
EXAMPLES:
sage: [Simplex(n).is_empty() for n in range(-1,4)]
[True, False, False, False, False]
Return True iff this simplex is a face of other.
EXAMPLES:
sage: Simplex(3).is_face(Simplex(5))
True
sage: Simplex(5).is_face(Simplex(2))
False
sage: Simplex(['a', 'b', 'c']).is_face(Simplex(8))
False
The join of this simplex with another one.
The join of two simplices ![[v_0, ..., v_k]](../../_images/math/667622c214dbe572cd4e9082e87ff5075cc8f0af.png) and
and ![[w_0, ...,
w_n]](../../_images/math/53a8d64d2398e996ef3ddd631beffe741897331b.png) is the simplex
is the simplex ![[v_0, ..., v_k, w_0, ..., w_n]](../../_images/math/e88cd2a00caa860daf45061271174c965277b5e5.png) .
.
| Parameters: |
|
|---|
EXAMPLES:
sage: Simplex(2).join(Simplex(3))
('L0', 'L1', 'L2', 'R0', 'R1', 'R2', 'R3')
sage: Simplex(['a', 'b']).join(Simplex(['x', 'y', 'z']))
('La', 'Lb', 'Rx', 'Ry', 'Rz')
sage: Simplex(['a', 'b']).join(Simplex(['x', 'y', 'z']), rename_vertices=False)
('a', 'b', 'x', 'y', 'z')
The product of this simplex with another one, as a list of simplices.
| Parameters: |
|
|---|
Algorithm: see Hatcher, p. 277-278 (who in turn refers to
Eilenberg-Steenrod, p. 68): given Simplex(m) and
Simplex(n), then Simplex(m) x Simplex(n) can be
triangulated as follows: for each path 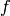 from
from 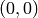 to
to
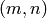 along the integer grid in the plane, going up or right
at each lattice point, associate an
along the integer grid in the plane, going up or right
at each lattice point, associate an 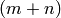 -simplex with
vertices
-simplex with
vertices 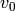 ,
, 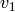 , ..., where
, ..., where 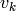 is the
is the  vertex
in the path
vertex
in the path 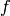 .
.
Note that there are 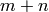 choose
choose  such paths. Note also
that each vertex in the product is a pair of vertices
such paths. Note also
that each vertex in the product is a pair of vertices  where
where  is a vertex in the left-hand factor and
is a vertex in the left-hand factor and 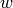 is a vertex in the right-hand factor.
is a vertex in the right-hand factor.
Note
This produces a list of simplices – not a Simplex, not a SimplicialComplex.
EXAMPLES:
sage: len(Simplex(2).product(Simplex(2)))
6
sage: Simplex(1).product(Simplex(1))
[('L0R0', 'L0R1', 'L1R1'), ('L0R0', 'L1R0', 'L1R1')]
sage: Simplex(1).product(Simplex(1), rename_vertices=False)
[((0, 0), (0, 1), (1, 1)), ((0, 0), (1, 0), (1, 1))]
REFERENCES:
The frozenset attached to this simplex.
EXAMPLES:
sage: Simplex(3).set()
frozenset([0, 1, 2, 3])
The tuple attached to this simplex.
EXAMPLES:
sage: Simplex(3).tuple()
(0, 1, 2, 3)
Although simplices are printed as if they were tuples, they are not the same type:
sage: type(Simplex(3).tuple())
<type 'tuple'>
sage: type(Simplex(3))
<class 'sage.homology.simplicial_complex.Simplex'>
Bases: sage.homology.cell_complex.GenericCellComplex
Define a simplicial complex.
| Parameters: |
|
|---|---|
| Returns: | a simplicial complex |
vertex_set may be a non-negative integer  (in which case
the simplicial complex will have
(in which case
the simplicial complex will have 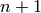 vertices
vertices 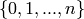 ), or it may be anything which may be converted to a tuple.
Call the elements of this ‘vertices’.
), or it may be anything which may be converted to a tuple.
Call the elements of this ‘vertices’.
maximal_faces should be a list or tuple or set (indeed, anything which may be converted to a set) whose elements are lists (or tuples, etc.) of vertices. Maximal faces are also known as ‘facets’.
If vertex_check is True, check to see that each given maximal face is a subset of the vertex set. Raise an error for any bad face.
If maximality_check is True, check that each maximal face is, in fact, maximal. In this case, when producing the internal representation of the simplicial complex, omit those that are not. It is highly recommended that this be True; various methods for this class may fail if faces which are claimed to be maximal are in fact not.
If sort_facets is True, sort the vertices in each facet. If the vertices in different facets are not ordered compatibly (e.g., if you have facets (1, 3, 5) and (5, 3, 8)), then homology calculations may have unpredictable results.
If name_check is True, check the names of the vertices to see if they can be easily converted to generators of a polynomial ring – use this if you plan to use the Stanley-Reisner ring for the simplicial complex.
Note
The elements of vertex_set are not automatically in the simplicial complex: each one is only included if it is a vertex of at least one of the specified facets.
EXAMPLES:
sage: SimplicialComplex(4, [[1,2], [1,4]])
Simplicial complex with vertex set (0, 1, 2, 3, 4) and facets {(1, 2), (1, 4)}
sage: SimplicialComplex(3, [[0,2], [0,3], [0]])
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(0, 2), (0, 3)}
sage: SimplicialComplex(3, [[0,2], [0,3], [0]], maximality_check=False)
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(0, 2), (0, 3), (0,)}
sage: S = SimplicialComplex(['a', 'b', 'c'], (('a', 'b'), ('a', 'c'), ('b', 'c')))
sage: S
Simplicial complex with vertex set ('a', 'b', 'c') and facets {('b', 'c'), ('a', 'c'), ('a', 'b')}
You can also omit the vertex_set argument – if the first argument is a list of lists (or anything similar – something which looks like it should be maximal_faces), then it is used for maximal_faces, and the set of vertices is deduced from the vertices used therein:
sage: SimplicialComplex([[0,2], [0,3], [0,6]])
Simplicial complex with vertex set (0, 2, 3, 6) and facets {(0, 6), (0, 2), (0, 3)}
TESTS:
sage: S = SimplicialComplex(['a', 'b', 'c'], (('a', 'b'), ('a', 'c'), ('b', 'c')))
sage: S == loads(dumps(S))
True
Add a face to this simplicial complex
| Parameter: | face – a subset of the vertex set |
|---|
This changes the simplicial complex, adding a new face and all of its subfaces.
EXAMPLES:
sage: X = SimplicialComplex(2, [[0,1], [0,2]])
sage: X.add_face([0,1,2,]); X
Simplicial complex with vertex set (0, 1, 2) and facets {(0, 1, 2)}
sage: Y = SimplicialComplex(3); Y
Simplicial complex with vertex set (0, 1, 2, 3) and facets {()}
sage: Y.add_face([0,1])
sage: Y.add_face([1,2,3])
sage: Y
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(1, 2, 3), (0, 1)}
If you add a face which is already present, there is no effect:
sage: Y.add_face([1,3]); Y
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(1, 2, 3), (0, 1)}
The Alexander dual of this simplicial complex: according to the Macaulay2 documentation, this is the simplicial complex whose faces are the complements of its nonfaces.
Thus find the minimal nonfaces and take their complements to find the facets in the Alexander dual.
EXAMPLES:
sage: Y = SimplicialComplex(4); Y
Simplicial complex with vertex set (0, 1, 2, 3, 4) and facets {()}
sage: Y.alexander_dual()
Simplicial complex with vertex set (0, 1, 2, 3, 4) and 5 facets
sage: X = SimplicialComplex(3, [[0,1], [1,2], [2,3], [3,0]])
sage: X.alexander_dual()
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(1, 3), (0, 2)}
The barycentric subdivision of this simplicial complex.
See http://en.wikipedia.org/wiki/Barycentric_subdivision for a definition.
EXAMPLES:
sage: triangle = SimplicialComplex(2, [[0,1], [1,2], [0, 2]])
sage: hexagon = triangle.barycentric_subdivision()
sage: hexagon
Simplicial complex with 6 vertices and 6 facets
sage: hexagon.homology(1) == triangle.homology(1)
True
Barycentric subdivisions can get quite large, since each
 -dimensional facet in the original complex produces
-dimensional facet in the original complex produces
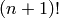 facets in the subdivision:
facets in the subdivision:
sage: S4 = simplicial_complexes.Sphere(4)
sage: S4
Simplicial complex with vertex set (0, 1, 2, 3, 4, 5) and 6 facets
sage: S4.barycentric_subdivision()
Simplicial complex with 62 vertices and 720 facets
Return the category to which this chain complex belongs: the category of all simplicial complexes.
EXAMPLES:
sage: SimplicialComplex(5, [[0,1], [1,2,3,4,5]]).category()
Category of simplicial complexes
The faces of this simplicial complex, in the form of a dictionary of sets keyed by dimension. If the optional argument subcomplex is present, then return only the faces which are not in the subcomplex.
| Parameter: | subcomplex (optional, default None) – a subcomplex of this simplicial complex. Return faces which are not in this subcomplex. |
|---|
EXAMPLES:
sage: Y = SimplicialComplex(5, [[1,2], [1,4]])
sage: Y.faces()
{0: set([(4,), (2,), (1,)]), 1: set([(1, 2), (1, 4)]), -1: set([()])}
sage: L = SimplicialComplex(5, [[1,2]])
sage: Y.faces(subcomplex=L)
{0: set([(4,)]), 1: set([(1, 4)]), -1: set([])}
The chain complex associated to this simplicial complex.
| Parameters: |
|
|---|
Note
If subcomplex is nonempty, then the argument augmented
has no effect: the chain complex relative to a nonempty
subcomplex is zero in dimension  .
.
EXAMPLES:
sage: circle = SimplicialComplex(2, [[0,1], [1,2], [0, 2]])
sage: circle.chain_complex()
Chain complex with at most 2 nonzero terms over Integer Ring
sage: circle.chain_complex()._latex_()
'\Bold{Z}^{3} \xrightarrow{d_{1}} \Bold{Z}^{3}'
sage: circle.chain_complex(base_ring=QQ, augmented=True)
Chain complex with at most 3 nonzero terms over Rational Field
The cone on this simplicial complex.
The cone is the simplicial complex formed by adding a new
vertex 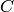 and simplices of the form
and simplices of the form ![[C, v_0, ..., v_k]](../../_images/math/965d465f2c17bbdc56454c318395dd6915107058.png) for
every simplex
for
every simplex ![[v_0, ..., v_k]](../../_images/math/667622c214dbe572cd4e9082e87ff5075cc8f0af.png) in the original simplicial
complex. That is, the cone is the join of the original
complex with a one-point simplicial complex.
in the original simplicial
complex. That is, the cone is the join of the original
complex with a one-point simplicial complex.
EXAMPLES:
sage: S = SimplicialComplex(1, [[0], [1]])
sage: S.cone()
Simplicial complex with vertex set ('L0', 'L1', 'R0') and facets {('L0', 'R0'), ('L1', 'R0')}
The connected sum of this simplicial complex with another one.
| Parameter: | other – another simplicial complex |
|---|---|
| Returns: | the connected sum self # other |
Warning
This does not check that self and other are manifolds, only that their facets all have the same dimension. Since a (more or less) random facet is chosen from each complex and then glued together, this method may return random results if applied to non-manifolds, depending on which facet is chosen.
Algorithm: a facet is chosen from each surface, and removed. The vertices of these two facets are relabeled to (0,1,...,dim). Of the remaining vertices, the ones from the left-hand factor are renamed by prepending an “L”, and similarly the remaining vertices in the right-hand factor are renamed by prepending an “R”.
EXAMPLES:
sage: S1 = simplicial_complexes.Sphere(1)
sage: S1.connected_sum(S1.connected_sum(S1)).homology()
{0: 0, 1: Z}
sage: P = simplicial_complexes.RealProjectivePlane(); P
Simplicial complex with vertex set (0, 1, 2, 3, 4, 5) and 10 facets
sage: P.connected_sum(P) # the Klein bottle
Simplicial complex with 9 vertices and 18 facets
The notation ‘+’ may be used for connected sum, also:
sage: P + P # the Klein bottle
Simplicial complex with 9 vertices and 18 facets
sage: (P + P).homology()[1]
Z x C2
Returns self as a 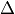 -complex. The
-complex. The 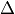 -complex
is essentially identical to the simplicial complex: it has
same simplices with the same boundaries.
-complex
is essentially identical to the simplicial complex: it has
same simplices with the same boundaries.
| Parameter: | sort_simplices (boolean; optional, default False) – if True, sort the list of simplices in each dimension |
|---|
EXAMPLES:
sage: T = simplicial_complexes.Torus()
sage: Td = T.delta_complex()
sage: Td
Delta complex with 7 vertices and 43 simplices
sage: T.homology() == Td.homology()
True
The disjoint union of this simplicial complex with another one.
| Parameters: |
|
|---|
EXAMPLES:
sage: S1 = simplicial_complexes.Sphere(1)
sage: S2 = simplicial_complexes.Sphere(2)
sage: S1.disjoint_union(S2).homology()
{0: Z, 1: Z, 2: Z}
The set of vertices belonging to some face. Returns a Simplex.
EXAMPLES:
sage: S = SimplicialComplex(15)
sage: S
Simplicial complex with 16 vertices and facets {()}
sage: S.effective_vertices()
()
sage: S = SimplicialComplex(15,[[0,1,2,3],[6,7]])
sage: S
Simplicial complex with 16 vertices and facets {(6, 7), (0, 1, 2, 3)}
sage: S.effective_vertices()
(0, 1, 2, 3, 6, 7)
sage: type(S.effective_vertices())
<class 'sage.homology.simplicial_complex.Simplex'>
The faces of this simplicial complex, in the form of a dictionary of sets keyed by dimension. If the optional argument subcomplex is present, then return only the faces which are not in the subcomplex.
| Parameter: | subcomplex (optional, default None) – a subcomplex of this simplicial complex. Return faces which are not in this subcomplex. |
|---|
EXAMPLES:
sage: Y = SimplicialComplex(5, [[1,2], [1,4]])
sage: Y.faces()
{0: set([(4,), (2,), (1,)]), 1: set([(1, 2), (1, 4)]), -1: set([()])}
sage: L = SimplicialComplex(5, [[1,2]])
sage: Y.faces(subcomplex=L)
{0: set([(4,)]), 1: set([(1, 4)]), -1: set([])}
The maximal faces (a.k.a. facets) of this simplicial complex.
This just returns the set of facets used in defining the simplicial complex, so if the simplicial complex was defined with no maximality checking, none is done here, either.
EXAMPLES:
sage: Y = SimplicialComplex(5, [[0,2], [1,4]])
sage: Y.maximal_faces()
{(1, 4), (0, 2)}
facets is a synonym for maximal_faces:
sage: S = SimplicialComplex(2, [[0,1], [0,1,2]])
sage: S.facets()
{(0, 1, 2)}
Returns the largest sub-simplicial complex of self containing exactly sub_vertex_set as vertices.
EXAMPLES:
sage: S = simplicial_complexes.Sphere(2)
sage: S
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(0, 2, 3), (0, 1, 2), (1, 2, 3), (0, 1, 3)}
sage: S.generated_subcomplex([0,1,2])
Simplicial complex with vertex set (0, 1, 2) and facets {(0, 1, 2)}
The 1-skeleton of this simplicial complex, as a graph.
Warning
This may give the wrong answer if the simplicial complex was constructed with maximality_check set to False.
EXAMPLES:
sage: S = SimplicialComplex(3, [[0,1,2,3]])
sage: G = S.graph(); G
Graph on 4 vertices
sage: G.edges()
[(0, 1, None), (0, 2, None), (0, 3, None), (1, 2, None), (1, 3, None), (2, 3, None)]
sage: S = SimplicialComplex(3,[[1,2,3],[1]],maximality_check=False)
sage: G = S.graph()
sage: G.is_connected()
False
sage: G.vertices() #random order
[1, 2, 3, (1,)]
sage: G.edges()
[(1, 2, None), (1, 3, None), (2, 3, None)]
Returns True if and only if self is connected.
Warning
This may give the wrong answer if the simplicial complex was constructed with maximality_check set to False. See the final example.
EXAMPLES:
sage: V = SimplicialComplex([0,1,2,3],[[0,1,2],[3]])
sage: V
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(0, 1, 2), (3,)}
sage: V.is_connected()
False
sage: X = SimplicialComplex([0,1,2,3],[[0,1,2]])
sage: X.is_connected()
True
sage: U = simplicial_complexes.ChessboardComplex(3,3)
sage: U.is_connected()
True
sage: W = simplicial_complexes.Sphere(3)
sage: W.is_connected()
True
sage: S = SimplicialComplex(4,[[0,1],[2,3]])
sage: S.is_connected()
False
sage: S = SimplicialComplex(2,[[0,1],[1],[0]],maximality_check=False)
sage: S.is_connected()
False
Returns True if and only if self is a flag complex.
A flag complex is a simplicial complex that is the largest simplicial complex on its 1-skeleton. Thus a flag complex is the clique complex of its graph.
EXAMPLES:
sage: h = Graph({0:[1,2,3,4],1:[2,3,4],2:[3]})
sage: x = h.clique_complex()
sage: x
Simplicial complex with vertex set (0, 1, 2, 3, 4) and facets {(0, 1, 4), (0, 1, 2, 3)}
sage: x.is_flag_complex()
True
sage: X = simplicial_complexes.ChessboardComplex(3,3)
sage: X.is_flag_complex()
True
True iff this simplicial complex is pure: a simplicial complex is pure iff all of its maximal faces have the same dimension.
Warning
This may give the wrong answer if the simplicial complex was constructed with maximality_check set to False.
EXAMPLES:
sage: U = SimplicialComplex(5, [[1,2], [1, 3, 4]])
sage: U.is_pure()
False
sage: X = SimplicialComplex(3, [[0,1], [0,2], [1,2]])
sage: X.is_pure()
True
The join of this simplicial complex with another one.
The join of two simplicial complexes 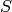 and
and 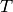 is the
simplicial complex
is the
simplicial complex 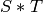 with simplices of the form
with simplices of the form ![[v_0,
..., v_k, w_0, ..., w_n]](../../_images/math/579d62a3cba2aade8dda074bc28b8fd7ad6f5fa1.png) for all simplices
for all simplices ![[v_0, ..., v_k]](../../_images/math/667622c214dbe572cd4e9082e87ff5075cc8f0af.png) in
in
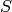 and
and ![[w_0, ..., w_n]](../../_images/math/f522ac0086a19ea0e89dbe2fbc57c846a80b67c6.png) in
in 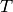 .
.
| Parameters: |
|
|---|
EXAMPLES:
sage: S = SimplicialComplex(1, [[0], [1]])
sage: T = SimplicialComplex([2, 3], [[2], [3]])
sage: S.join(T)
Simplicial complex with vertex set ('L0', 'L1', 'R2', 'R3') and 4 facets
sage: S.join(T, rename_vertices=False)
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(1, 3), (1, 2), (0, 2), (0, 3)}
The notation ‘*’ may be used, as well:
sage: S * S
Simplicial complex with vertex set ('L0', 'L1', 'R0', 'R1') and 4 facets
sage: S * S * S * S * S * S * S * S
Simplicial complex with 16 vertices and 256 facets
The link of a simplex in this simplicial complex.
The link of a simplex 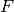 is the simplicial complex formed by
all simplices
is the simplicial complex formed by
all simplices 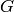 which are disjoint from
which are disjoint from 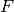 but for which
but for which  is a simplex.
is a simplex.
| Parameter: | simplex – a simplex in this simplicial complex. |
|---|
EXAMPLES:
sage: X = SimplicialComplex(4, [[0,1,2], [1,2,3]])
sage: X.link(Simplex([0]))
Simplicial complex with vertex set (0, 1, 2, 3, 4) and facets {(1, 2)}
sage: X.link([1,2])
Simplicial complex with vertex set (0, 1, 2, 3, 4) and facets {(3,), (0,)}
sage: Y = SimplicialComplex(3, [[0,1,2,3]])
sage: Y.link([1])
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(0, 2, 3)}
The maximal faces (a.k.a. facets) of this simplicial complex.
This just returns the set of facets used in defining the simplicial complex, so if the simplicial complex was defined with no maximality checking, none is done here, either.
EXAMPLES:
sage: Y = SimplicialComplex(5, [[0,2], [1,4]])
sage: Y.maximal_faces()
{(1, 4), (0, 2)}
facets is a synonym for maximal_faces:
sage: S = SimplicialComplex(2, [[0,1], [0,1,2]])
sage: S.facets()
{(0, 1, 2)}
Set consisting of the minimal subsets of the vertex set of this simplicial complex which do not form faces.
Algorithm: first take the complement (within the vertex set)
of each facet, obtaining a set 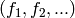 of simplices.
Now form the set of all simplices of the form
of simplices.
Now form the set of all simplices of the form 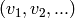 where vertex
where vertex 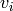 is in face
is in face 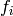 . This set will
contain the minimal nonfaces and may contain some non-minimal
nonfaces also, so loop through the set to find the minimal
ones. (The last two steps are taken care of by the
_transpose_simplices routine.)
. This set will
contain the minimal nonfaces and may contain some non-minimal
nonfaces also, so loop through the set to find the minimal
ones. (The last two steps are taken care of by the
_transpose_simplices routine.)
This is used in computing the Stanley-Reisner ring and the Alexander dual.
EXAMPLES:
sage: X = SimplicialComplex(4)
sage: X.minimal_nonfaces()
{(4,), (2,), (3,), (0,), (1,)}
sage: X.add_face([1,2])
sage: X.add_face([1,3])
sage: X.minimal_nonfaces()
{(4,), (2, 3), (0,)}
sage: Y = SimplicialComplex(3, [[0,1], [1,2], [2,3], [3,0]])
sage: Y.minimal_nonfaces()
{(1, 3), (0, 2)}
The set of simplices of dimension n of this simplicial complex. If the optional argument subcomplex is present, then return the n-dimensional faces which are not in the subcomplex.
| Parameters: |
|
|---|
EXAMPLES:
sage: S = Set(range(1,5))
sage: Z = SimplicialComplex(S, S.subsets())
sage: Z
Simplicial complex with vertex set (1, 2, 3, 4) and facets {(1, 2, 3, 4)}
sage: Z.n_faces(2)
set([(1, 3, 4), (1, 2, 3), (2, 3, 4), (1, 2, 4)])
sage: K = SimplicialComplex(S, [[1,2,3], [2,3,4]])
sage: Z.n_faces(2, subcomplex=K)
set([(1, 3, 4), (1, 2, 4)])
The  -skeleton of this simplicial complex: the simplicial
complex obtained by discarding all of the simplices in
dimensions larger than
-skeleton of this simplicial complex: the simplicial
complex obtained by discarding all of the simplices in
dimensions larger than  .
.
| Parameter: | n – non-negative integer |
|---|
EXAMPLES:
sage: X = SimplicialComplex(3, [[0,1], [1,2,3], [0,2,3]])
sage: X.n_skeleton(1)
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(2, 3), (0, 2), (1, 3), (1, 2), (0, 3), (0, 1)}
sage: X.n_skeleton(2)
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(0, 2, 3), (1, 2, 3), (0, 1)}
The product of this simplicial complex with another one.
| Parameters: |
|
|---|
The vertices in the product will be the set of ordered pairs
 where
where  is a vertex in self and
is a vertex in self and 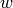 is a vertex in
right.
is a vertex in
right.
Warning
If X and Y are simplicial complexes, then X*Y returns their join, not their product.
EXAMPLES:
sage: S = SimplicialComplex(3, [[0,1], [1,2], [0,2]]) # circle
sage: K = SimplicialComplex(1, [[0,1]]) # edge
sage: S.product(K).vertices() # cylinder
('L0R0', 'L0R1', 'L1R0', 'L1R1', 'L2R0', 'L2R1', 'L3R0', 'L3R1')
sage: S.product(K, rename_vertices=False).vertices()
((0, 0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1), (3, 0), (3, 1))
sage: T = S.product(S) # torus
sage: T
Simplicial complex with 16 vertices and 18 facets
sage: T.homology()
{0: 0, 1: Z x Z, 2: Z}
These can get large pretty quickly:
sage: T = simplicial_complexes.Torus(); T
Simplicial complex with vertex set (0, 1, 2, 3, 4, 5, 6) and 14 facets
sage: K = simplicial_complexes.KleinBottle(); K
Simplicial complex with 9 vertices and 18 facets
sage: T.product(K) # long time: 5 or 6 seconds
Simplicial complex with 63 vertices and 1512 facets
Remove a face from this simplicial complex
| Parameter: | face – a face of the simplicial complex |
|---|
This changes the simplicial complex, removing the given face any face which contains it.
Algorithm: check if the face is a facet. If so, simply add its faces and remove it. Otherwise, take the Alexander dual, add the complement of face, and then take the Alexander dual again.
EXAMPLES:
sage: S = range(1,5)
sage: Z = SimplicialComplex(S, [S]); Z
Simplicial complex with vertex set (1, 2, 3, 4) and facets {(1, 2, 3, 4)}
sage: Z.remove_face([1,2])
sage: Z
Simplicial complex with vertex set (1, 2, 3, 4) and facets {(1, 3, 4), (2, 3, 4)}
sage: S = SimplicialComplex(4,[[0,1,2],[2,3]])
sage: S
Simplicial complex with vertex set (0, 1, 2, 3, 4) and facets {(0, 1, 2), (2, 3)}
sage: S.remove_face([0,1,2])
sage: S
Simplicial complex with vertex set (0, 1, 2, 3, 4) and facets {(1, 2), (2, 3), (0, 2), (0, 1)}
The Stanley-Reisner ring of this simplicial complex.
| Parameter: | base_ring (optional, default ZZ) – a commutative ring |
|---|---|
| Returns: | a quotient of a polynomial algebra with coefficients in base_ring, with one generator for each vertex in the simplicial complex, by the ideal generated by the products of those vertices which do not form faces in it. |
Thus the ideal is generated by the products corresponding to the minimal nonfaces of the simplicial complex.
Warning
This may be quite slow!
Also, this may behave badly if the vertices have the ‘wrong’ names. To avoid this, define the simplicial complex at the start with the flag name_check set to True.
More precisely, this is a quotient of a polynomial ring with one generator for each vertex. If the name of a vertex is a non-negative integer, then the corresponding polynomial generator is named ‘x’ followed by that integer (e.g., ‘x2’, ‘x3’, ‘x5’, ...). Otherwise, the polynomial generators are given the same names as the vertices. Thus if the vertex set is (2, ‘x2’), there will be problems.
EXAMPLES:
sage: X = SimplicialComplex(3, [[0,1], [1,2], [2,3], [0,3]])
sage: X.stanley_reisner_ring()
Quotient of Multivariate Polynomial Ring in x0, x1, x2, x3 over Integer Ring by the ideal (x1*x3, x0*x2)
sage: Y = SimplicialComplex(4); Y
Simplicial complex with vertex set (0, 1, 2, 3, 4) and facets {()}
sage: Y.stanley_reisner_ring()
Quotient of Multivariate Polynomial Ring in x0, x1, x2, x3, x4 over Integer Ring by the ideal (x4, x2, x3, x0, x1)
sage: Y.add_face([0,1,2,3,4])
sage: Y.stanley_reisner_ring(base_ring=QQ)
Quotient of Multivariate Polynomial Ring in x0, x1, x2, x3, x4 over Rational Field by the ideal (0)
The suspension of this simplicial complex.
| Parameter: | n (optional, default 1) – positive integer – suspend this many times. |
|---|
The suspension is the simplicial complex formed by adding two
new vertices  and
and 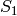 and simplices of the form
and simplices of the form ![[S_0,
v_0, ..., v_k]](../../_images/math/d939275d8908888c623f1fb898b63e95166fd86c.png) and
and ![[S_1, v_0, ..., v_k]](../../_images/math/c13ce6f9dc3a1f6e60bcb457b93877aef7e6d0f8.png) for every simplex
for every simplex
![[v_0, ..., v_k]](../../_images/math/667622c214dbe572cd4e9082e87ff5075cc8f0af.png) in the original simplicial complex. That
is, the suspension is the join of the original complex with a
two-point simplicial complex.
in the original simplicial complex. That
is, the suspension is the join of the original complex with a
two-point simplicial complex.
EXAMPLES:
sage: S = SimplicialComplex(1, [[0], [1]])
sage: S.suspension()
Simplicial complex with vertex set ('L0', 'L1', 'R0', 'R1') and 4 facets
sage: S3 = S.suspension(3) # the 3-sphere
sage: S3.homology()
{0: 0, 1: 0, 2: 0, 3: Z}
The vertex set of this simplicial complex.
EXAMPLES:
sage: S = SimplicialComplex(15, [[0,1], [1,2]])
sage: S
Simplicial complex with 16 vertices and facets {(1, 2), (0, 1)}
sage: S.vertices()
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15)
Note that this actually returns a simplex:
sage: type(S.vertices())
<class 'sage.homology.simplicial_complex.Simplex'>
The wedge (one-point union) of this simplicial complex with another one.
| Parameters: |
|
|---|
Note
This operation is not well-defined if self or other is not path-connected.
EXAMPLES:
sage: S1 = simplicial_complexes.Sphere(1)
sage: S2 = simplicial_complexes.Sphere(2)
sage: S1.wedge(S2).homology()
{0: 0, 1: Z, 2: Z}
Given lists (or tuples or ...) t1 and t2, think of them as labelings for vertices: t1 labeling points on the x-axis, t2 labeling points on the y-axis, both increasing. Return the list of rectilinear paths along the grid defined by these points in the plane, starting from (t1[0], t2[0]), ending at (t1[last], t2[last]), and at each grid point, going either right or up. See the examples.
| Parameters: |
|
|---|---|
| Returns: | list of lists of vertices making up the paths as described above |
| Return type: | list of lists |
This is used when triangulating the product of simplices. The
optional argument length is used for 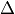 -complexes, to
specify all simplices in a product: in the triangulation of a
product of two simplices, there is a
-complexes, to
specify all simplices in a product: in the triangulation of a
product of two simplices, there is a 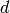 -simplex for every path of
length
-simplex for every path of
length 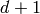 in the lattice. The path must start at the bottom
left and end at the upper right, and it must use at least one
point in each row and in each column, so if length is too
small, there will be no paths.
in the lattice. The path must start at the bottom
left and end at the upper right, and it must use at least one
point in each row and in each column, so if length is too
small, there will be no paths.
EXAMPLES:
sage: from sage.homology.simplicial_complex import lattice_paths
sage: lattice_paths([0,1,2], [0,1,2])
[[(0, 0), (0, 1), (0, 2), (1, 2), (2, 2)],
[(0, 0), (0, 1), (1, 1), (1, 2), (2, 2)],
[(0, 0), (1, 0), (1, 1), (1, 2), (2, 2)],
[(0, 0), (0, 1), (1, 1), (2, 1), (2, 2)],
[(0, 0), (1, 0), (1, 1), (2, 1), (2, 2)],
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2)]]
sage: lattice_paths(('a', 'b', 'c'), (0, 3, 5))
[[('a', 0), ('a', 3), ('a', 5), ('b', 5), ('c', 5)],
[('a', 0), ('a', 3), ('b', 3), ('b', 5), ('c', 5)],
[('a', 0), ('b', 0), ('b', 3), ('b', 5), ('c', 5)],
[('a', 0), ('a', 3), ('b', 3), ('c', 3), ('c', 5)],
[('a', 0), ('b', 0), ('b', 3), ('c', 3), ('c', 5)],
[('a', 0), ('b', 0), ('c', 0), ('c', 3), ('c', 5)]]
sage: lattice_paths(range(3), range(3), length=2)
[]
sage: lattice_paths(range(3), range(3), length=3)
[[(0, 0), (1, 1), (2, 2)]]
sage: lattice_paths(range(3), range(3), length=4)
[[(0, 0), (1, 1), (1, 2), (2, 2)],
[(0, 0), (0, 1), (1, 2), (2, 2)],
[(0, 0), (1, 1), (2, 1), (2, 2)],
[(0, 0), (1, 0), (2, 1), (2, 2)],
[(0, 0), (0, 1), (1, 1), (2, 2)],
[(0, 0), (1, 0), (1, 1), (2, 2)]]
Rename a vertex: the vertices from the list ‘keep’ get relabeled 0, 1, 2, ..., in order. Any other vertex (e.g. 4) gets renamed to by prepending an ‘L’ or an ‘R’ (thus to either ‘L4’ or ‘R4’), depending on whether the argument left is True or False.
| Parameters: |
|
|---|
This is used by the connected_sum method for simplicial complexes.
EXAMPLES:
sage: from sage.homology.simplicial_complex import rename_vertex
sage: rename_vertex(6, [5, 6, 7])
1
sage: rename_vertex(3, [5, 6, 7, 8, 9])
'L3'
sage: rename_vertex(3, [5, 6, 7], left=False)
'R3'