AUTHORS:
This file constructs some examples of simplicial complexes. There are two main types: surfaces and examples related to graph theory.
For surfaces (and other manifolds), there are functions defining the 2-sphere, the n-sphere for any n, the torus, the real projective plane, the Klein bottle, and surfaces of arbitrary genus, all as simplicial complexes.
Aside from surfaces, this file also provides some functions for constructing some other simplicial complexes: the simplicial complex of not-i-connected graphs on n vertices, the matching complex on n vertices, and the chessboard complex for an n by i chessboard. These provide examples of large simplicial complexes; for example, not_i_connected_graphs(7,2) has over a million simplices.
All of these examples are accessible by typing “simplicial_complexes.NAME”, where “NAME” is the name of the example; you can get a list by typing “simplicial_complexes.” and hitting the TAB key:
Sphere
Simplex
Torus
RealProjectivePlane
KleinBottle
SurfaceOfGenus
MooreSpace
NotIConnectedGraphs
MatchingComplex
ChessboardComplex
RandomComplex
See the documentation for simplicial_complexes and for each particular type of example for full details.
Some examples of simplicial complexes.
Here are the available examples; you can also type “simplicial_complexes.” and hit tab to get a list:
Sphere
Simplex
Torus
RealProjectivePlane
KleinBottle
SurfaceOfGenus
MooreSpace
NotIConnectedGraphs
MatchingComplex
ChessboardComplex
RandomComplex
EXAMPLES:
sage: S = simplicial_complexes.Sphere(2) # the 2-sphere
sage: S.homology()
{0: 0, 1: 0, 2: Z}
sage: simplicial_complexes.SurfaceOfGenus(3)
Simplicial complex with 15 vertices and 38 facets
sage: M4 = simplicial_complexes.MooreSpace(4)
sage: M4.homology()
{0: 0, 1: C4, 2: 0}
sage: simplicial_complexes.MatchingComplex(6).homology()
{0: 0, 1: Z^16, 2: 0}
The chessboard complex for an n by i chessboard.
Fix integers 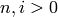 and consider sets
and consider sets 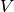 of
of  vertices
and
vertices
and 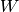 of
of  vertices. A ‘partial matching’ between
vertices. A ‘partial matching’ between 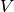 and
and
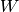 is a graph formed by edges
is a graph formed by edges 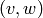 with
with 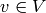 and
and 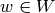 so that each vertex is in at most one edge. If
so that each vertex is in at most one edge. If  is
a partial matching, then so is any graph obtained by deleting
edges from
is
a partial matching, then so is any graph obtained by deleting
edges from  . Thus the set of all partial matchings on
. Thus the set of all partial matchings on 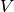 and
and 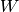 , viewed as a set of subsets of the
, viewed as a set of subsets of the 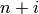 choose 2
possible edges, is closed under taking subsets, and thus forms
a simplicial complex called the ‘chessboard complex’. This
function produces that simplicial complex. (It is called the
chessboard complex because such graphs also correspond to ways
of placing rooks on an
choose 2
possible edges, is closed under taking subsets, and thus forms
a simplicial complex called the ‘chessboard complex’. This
function produces that simplicial complex. (It is called the
chessboard complex because such graphs also correspond to ways
of placing rooks on an  by
by  chessboard so that none of
them are attacking each other.)
chessboard so that none of
them are attacking each other.)
INPUT:
See Dumas et al. for information on computing its homology by computer, and see Wachs for an expository article about the theory.
EXAMPLES:
sage: C = simplicial_complexes.ChessboardComplex(5,5)
sage: C.f_vector()
[1, 25, 200, 600, 600, 120]
sage: simplicial_complexes.ChessboardComplex(3,3).homology()
{0: 0, 1: Z x Z x Z x Z, 2: 0}
REFERENCES:
A triangulation of the Klein bottle, formed by taking the connected sum of a real projective plane with itself. (This is not a minimal triangulation.)
EXAMPLES:
sage: simplicial_complexes.KleinBottle()
Simplicial complex with 9 vertices and 18 facets
The matching complex of graphs on n vertices.
Fix an integer 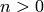 and consider a set
and consider a set 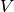 of
of  vertices.
A ‘partial matching’ on
vertices.
A ‘partial matching’ on 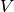 is a graph formed by edges so that
each vertex is in at most one edge. If
is a graph formed by edges so that
each vertex is in at most one edge. If  is a partial
matching, then so is any graph obtained by deleting edges from
is a partial
matching, then so is any graph obtained by deleting edges from
 . Thus the set of all partial matchings on
. Thus the set of all partial matchings on  vertices,
viewed as a set of subsets of the
vertices,
viewed as a set of subsets of the  choose 2 possible edges,
is closed under taking subsets, and thus forms a simplicial
complex called the ‘matching complex’. This function produces
that simplicial complex.
choose 2 possible edges,
is closed under taking subsets, and thus forms a simplicial
complex called the ‘matching complex’. This function produces
that simplicial complex.
INPUT:
See Dumas et al. for information on computing its homology by
computer, and see Wachs for an expository article about the
theory. For example, the homology of these complexes seems to
have only mod 3 torsion, and this has been proved for the
bottom non-vanishing homology group for the matching complex
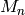 .
.
EXAMPLES:
sage: M = simplicial_complexes.MatchingComplex(7)
sage: H = M.homology()
sage: H
{0: 0, 1: C3, 2: Z^20}
sage: H[2].ngens()
20
sage: simplicial_complexes.MatchingComplex(8).homology(2) # long time (a few seconds)
Z^132
REFERENCES:
Triangulation of the mod q Moore space.
INPUT:
This is a simplicial complex with simplices of dimension 0, 1,
and 2, such that its reduced homology is isomorphic to
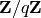 in dimension 1, zero otherwise.
in dimension 1, zero otherwise.
If 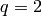 , this is the real projective plane. If
, this is the real projective plane. If 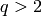 , then
construct it as follows: start with a triangle with vertices
1, 2, 3. We take a
, then
construct it as follows: start with a triangle with vertices
1, 2, 3. We take a 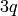 -gon forming a
-gon forming a  -fold cover of the
triangle, and we form the resulting complex as an
identification space of the
-fold cover of the
triangle, and we form the resulting complex as an
identification space of the 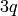 -gon. To triangulate this
identification space, put
-gon. To triangulate this
identification space, put  vertices
vertices 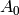 , ...,
, ..., 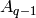 ,
in the interior, each of which is connected to 1, 2, 3 (two
facets each:
,
in the interior, each of which is connected to 1, 2, 3 (two
facets each: ![[1, 2, A_i]](../../_images/math/dfbfc370e62014e792b744cd444f53a234db1720.png) ,
, ![[2, 3, A_i]](../../_images/math/b5c5dbc97404e35ae7e8c1d711755809bd0ed9e0.png) ). Put
). Put  more
vertices in the interior:
more
vertices in the interior: 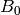 , ...,
, ..., 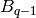 , with facets
, with facets
![[3, 1, B_i]](../../_images/math/bb4220df8601951fde430dd51532088b64975ac1.png) ,
, ![[3, B_i, A_i]](../../_images/math/f2be7efdd110480563724494fa159454894631a3.png) ,
, ![[1, B_i, A_{i+1}]](../../_images/math/e02f1246ca8cf4bf71facdf0811903dd69e6dfb5.png) ,
, ![[B_i,
A_i, A_{i+1}]](../../_images/math/6047ce3bcd339c385834d7b80096ed4598de2ff4.png) . Then triangulate the interior polygon with
vertices
. Then triangulate the interior polygon with
vertices 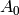 ,
, 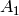 , ...,
, ..., 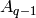 .
.
EXAMPLES:
sage: simplicial_complexes.MooreSpace(3).homology()[1]
C3
sage: simplicial_complexes.MooreSpace(4).suspension().homology()[2]
C4
sage: simplicial_complexes.MooreSpace(8)
Simplicial complex with 19 vertices and 54 facets
The simplicial complex of all graphs on n vertices which are not i-connected.
Fix an integer 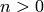 and consider the set of graphs on
and consider the set of graphs on  vertices. View each graph as its set of edges, so it is a
subset of a set of size
vertices. View each graph as its set of edges, so it is a
subset of a set of size  choose 2. A graph is
choose 2. A graph is
 -connected if, for any
-connected if, for any 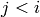 , if any
, if any 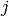 vertices are
removed along with the edges emanating from them, then the
graph remains connected. Now fix
vertices are
removed along with the edges emanating from them, then the
graph remains connected. Now fix  : it is clear that if
: it is clear that if  is not
is not  -connected, then the same is true for any graph
obtained from
-connected, then the same is true for any graph
obtained from  by deleting edges. Thus the set of all
graphs which are not
by deleting edges. Thus the set of all
graphs which are not  -connected, viewed as a set of subsets
of the
-connected, viewed as a set of subsets
of the  choose 2 possible edges, is closed under taking
subsets, and thus forms a simplicial complex. This function
produces that simplicial complex.
choose 2 possible edges, is closed under taking
subsets, and thus forms a simplicial complex. This function
produces that simplicial complex.
INPUT:
 at most
at most 
See Dumas et al. for information on computing its homology by
computer, and see Babson et al. for theory. For example,
Babson et al. show that when 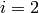 , the reduced homology of
this complex is nonzero only in dimension
, the reduced homology of
this complex is nonzero only in dimension 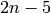 , where it is
free abelian of rank
, where it is
free abelian of rank 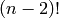 .
.
EXAMPLES:
sage: simplicial_complexes.NotIConnectedGraphs(5,2).f_vector()
[1, 10, 45, 120, 210, 240, 140, 20]
sage: simplicial_complexes.NotIConnectedGraphs(5,2).homology(5).ngens()
6
REFERENCES:
A minimal triangulation of the real projective plane.
EXAMPLES:
sage: P = simplicial_complexes.RealProjectivePlane()
sage: Q = simplicial_complexes.ProjectivePlane()
sage: P == Q
True
sage: P.cohomology(1)
0
sage: P.cohomology(2)
C2
sage: P.cohomology(1, base_ring=GF(2))
Vector space of dimension 1 over Finite Field of size 2
sage: P.cohomology(2, base_ring=GF(2))
Vector space of dimension 1 over Finite Field of size 2
A random d-dimensional simplicial complex on n vertices.
INPUT:
A random 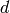 -dimensional simplicial complex on
-dimensional simplicial complex on  vertices,
as defined for example by Meshulam and Wallach, is constructed
as follows: take
vertices,
as defined for example by Meshulam and Wallach, is constructed
as follows: take  vertices and include all of the simplices
of dimension strictly less than
vertices and include all of the simplices
of dimension strictly less than 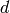 , and then for each
possible simplex of dimension
, and then for each
possible simplex of dimension 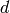 , include it with probability
, include it with probability
 .
.
EXAMPLES:
sage: simplicial_complexes.RandomComplex(6, 2)
Simplicial complex with vertex set (0, 1, 2, 3, 4, 5, 6) and 15 facets
If 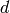 is too large (if
is too large (if 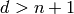 , so that there are no
, so that there are no
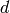 -dimensional simplices), then return the simplicial complex
with a single
-dimensional simplices), then return the simplicial complex
with a single 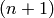 -dimensional simplex:
-dimensional simplex:
sage: simplicial_complexes.RandomComplex(6,12)
Simplicial complex with vertex set (0, 1, 2, 3, 4, 5, 6, 7) and facets {(0, 1, 2, 3, 4, 5, 6, 7)}
REFERENCES:
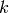 -dimensional complexes”, preprint, math.CO/0609773.
-dimensional complexes”, preprint, math.CO/0609773.A minimal triangulation of the real projective plane.
EXAMPLES:
sage: P = simplicial_complexes.RealProjectivePlane()
sage: Q = simplicial_complexes.ProjectivePlane()
sage: P == Q
True
sage: P.cohomology(1)
0
sage: P.cohomology(2)
C2
sage: P.cohomology(1, base_ring=GF(2))
Vector space of dimension 1 over Finite Field of size 2
sage: P.cohomology(2, base_ring=GF(2))
Vector space of dimension 1 over Finite Field of size 2
An  -dimensional simplex, as a simplicial complex.
-dimensional simplex, as a simplicial complex.
INPUT:
OUTPUT: the simplicial complex consisting of the  -simplex
on vertices
-simplex
on vertices 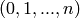 and all of its faces.
and all of its faces.
EXAMPLES:
sage: simplicial_complexes.Simplex(3)
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(0, 1, 2, 3)}
sage: simplicial_complexes.Simplex(5).euler_characteristic()
1
A minimal triangulation of the n-dimensional sphere.
INPUT:
EXAMPLES:
sage: simplicial_complexes.Sphere(2)
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(0, 2, 3), (0, 1, 2), (1, 2, 3), (0, 1, 3)}
sage: simplicial_complexes.Sphere(5).homology()
{0: 0, 1: 0, 2: 0, 3: 0, 4: 0, 5: Z}
sage: [simplicial_complexes.Sphere(n).euler_characteristic() for n in range(6)]
[2, 0, 2, 0, 2, 0]
sage: [simplicial_complexes.Sphere(n).f_vector() for n in range(6)]
[[1, 2],
[1, 3, 3],
[1, 4, 6, 4],
[1, 5, 10, 10, 5],
[1, 6, 15, 20, 15, 6],
[1, 7, 21, 35, 35, 21, 7]]
A surface of genus g.
INPUT:
In the orientable case, return a sphere if 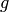 is zero, and
otherwise return a
is zero, and
otherwise return a 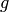 -fold connected sum of a torus with
itself.
-fold connected sum of a torus with
itself.
In the non-orientable case, raise an error if 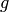 is zero. If
is zero. If
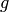 is positive, return a
is positive, return a 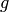 -fold connected sum of a
real projective plane with itself.
-fold connected sum of a
real projective plane with itself.
EXAMPLES:
sage: simplicial_complexes.SurfaceOfGenus(2)
Simplicial complex with 11 vertices and 26 facets
sage: simplicial_complexes.SurfaceOfGenus(1, orientable=False)
Simplicial complex with vertex set (0, 1, 2, 3, 4, 5) and 10 facets
A minimal triangulation of the torus.
EXAMPLES:
sage: simplicial_complexes.Torus().homology(1)
Z x Z
List of maximal matchings between the sets A and B: a matching is a set of pairs (a,b) in A x B where each a, b appears in at most one pair. A maximal matching is one which is maximal with respect to inclusion of subsets of A x B.
INPUT:
EXAMPLES:
sage: from sage.homology.examples import matching
sage: matching([1,2], [3,4])
[set([(1, 3), (2, 4)]), set([(2, 3), (1, 4)])]
sage: matching([0,2], [0])
[set([(0, 0)]), set([(2, 0)])]