AUTHORS:
This module implements chain complexes of free 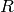 -modules, for any
commutative ring
-modules, for any
commutative ring 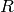 (although the interesting things, like homology,
only work if
(although the interesting things, like homology,
only work if 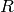 is the integers or a field).
is the integers or a field).
Fix a ring 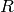 . A chain complex over
. A chain complex over 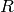 is a collection of
is a collection of
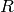 -modules
-modules 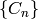 indexed by the integers, with
indexed by the integers, with 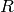 -module maps
-module maps
 such that
such that 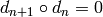 for
all
for
all  . The maps
. The maps 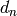 are called differentials.
are called differentials.
One can vary this somewhat: the differentials may decrease degree by
one instead of increasing it: sometimes a chain complex is defined
with 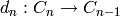 for each
for each  . Indeed, the
differentials may change dimension by any fixed integer.
. Indeed, the
differentials may change dimension by any fixed integer.
Also, the modules may be indexed over an abelian group other than the
integers, e.g., 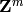 for some integer
for some integer 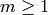 , in which
case the differentials may change the grading by any element of that
grading group.
, in which
case the differentials may change the grading by any element of that
grading group.
In this implementation, the ring 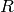 must be commutative and the
modules
must be commutative and the
modules 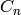 must be free
must be free 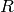 -modules. As noted above, homology
calculations will only work if the ring
-modules. As noted above, homology
calculations will only work if the ring 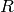 is either
is either  or a field.
The modules may be indexed by any free abelian group. The
differentials may increase degree by 1 or decrease it, or indeed
change it by any fixed amount: this is controlled by the degree
parameter used in defining the chain complex.
or a field.
The modules may be indexed by any free abelian group. The
differentials may increase degree by 1 or decrease it, or indeed
change it by any fixed amount: this is controlled by the degree
parameter used in defining the chain complex.
Bases: sage.structure.sage_object.SageObject
Define a chain complex.
INPUT:
OUTPUT: a chain complex
Warning
Right now, homology calculations will only work if the base ring is either ZZ or a field, so please take this into account when defining a chain complex.
Use data to define the chain complex. This may be in any of the following forms.
 . (Note that the shape of the matrix then determines the
rank of the free modules
. (Note that the shape of the matrix then determines the
rank of the free modules 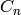 and
and 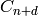 .)
.)![[C_0, d_0, C_1, d_1, C_2, d_2,
...]](../../_images/math/a0139b3975f85769bdf61360bf1f734e77ec54e0.png) , where each
, where each 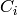 is a free module and each
is a free module and each 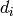 is a
matrix, as above. This only makes sense if grading_group
is
is a
matrix, as above. This only makes sense if grading_group
is  and degree is 1.
and degree is 1.![[r_0, d_0, r_1, d_1, r_2, d_2,
...]](../../_images/math/9c12565a6ec76e5060af95a8c1754344f4789095.png) , where
, where 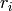 is the rank of the free module
is the rank of the free module 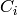 and
each
and
each 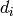 is a matrix, as above. This only makes sense if
grading_group is
is a matrix, as above. This only makes sense if
grading_group is  and degree is 1.
and degree is 1.![[d_0, d_1, d_2, ...]](../../_images/math/f69e93a11aabf14270c847d8c3748320d07e2e38.png) where each
where each
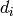 is a matrix, as above. This only makes sense if
grading_group is
is a matrix, as above. This only makes sense if
grading_group is  and degree is 1.
and degree is 1.Note
In fact, the free modules 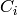 in case 2 and the ranks
in case 2 and the ranks 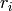 in case 3 are ignored: only the matrices are kept, and from
their shapes, the ranks of the modules are determined.
(Indeed, if data is a list or tuple, then any element which
is not a matrix is discarded; thus the list may have any number
of different things in it, and all of the non-matrices will be
ignored.) No error checking is done to make sure, for
instance, that the given modules have the appropriate ranks for
the given matrices. However, as long as check_products is
True, the code checks to see if the matrices are composable and
that each appropriate composite is zero.
in case 3 are ignored: only the matrices are kept, and from
their shapes, the ranks of the modules are determined.
(Indeed, if data is a list or tuple, then any element which
is not a matrix is discarded; thus the list may have any number
of different things in it, and all of the non-matrices will be
ignored.) No error checking is done to make sure, for
instance, that the given modules have the appropriate ranks for
the given matrices. However, as long as check_products is
True, the code checks to see if the matrices are composable and
that each appropriate composite is zero.
If the base ring is not specified, then the matrices are examined to determine a ring over which they are all naturally defined, and this becomes the base ring for the complex. If no such ring can be found, an error is raised. If the base ring is specified, then the matrices are converted automatically to this ring when defining the chain complex. If some matrix cannot be converted, then an error is raised.
EXAMPLES:
sage: ChainComplex()
Chain complex with at most 0 nonzero terms over Integer Ring
sage: C = ChainComplex({0: matrix(ZZ, 2, 3, [3, 0, 0, 0, 0, 0])})
sage: C
Chain complex with at most 2 nonzero terms over Integer Ring
sage: D = ChainComplex([matrix(ZZ, 2, 2, [0, 1, 0, 0]), matrix(ZZ, 2, 2, [0, 1, 0, 0])], base_ring=GF(2)); D
Chain complex with at most 3 nonzero terms over Finite Field of size 2
sage: D == loads(dumps(D))
True
Note that when a chain complex is defined in Sage, new differentials may be created: every nonzero module in the chain complex must have a differential coming from it, even if that differential is zero:
sage: IZ = ChainComplex({0: identity_matrix(ZZ, 1)})
sage: IZ.differential() # the differentials in the chain complex
{0: [1], 1: []}
sage: IZ.differential(1).parent()
Full MatrixSpace of 0 by 1 dense matrices over Integer Ring
sage: mat = ChainComplex({0: matrix(ZZ, 3, 4)}).differential(1)
sage: mat.nrows(), mat.ncols()
(0, 3)
Defining the base ring implicitly:
sage: ChainComplex([matrix(QQ, 3, 1), matrix(ZZ, 4, 3)])
Chain complex with at most 3 nonzero terms over Rational Field
sage: ChainComplex([matrix(GF(125, 'a'), 3, 1), matrix(ZZ, 4, 3)])
Chain complex with at most 3 nonzero terms over Finite Field in a of size 5^3
If the matrices are defined over incompatible rings, an error results:
sage: ChainComplex([matrix(GF(125, 'a'), 3, 1), matrix(QQ, 4, 3)])
...
TypeError: unable to find a common ring for all elements
If the base ring is given explicitly but is not compatible with the matrices, an error results:
sage: ChainComplex([matrix(GF(125, 'a'), 3, 1)], base_ring=QQ)
...
TypeError: Unable to coerce 0 (<type 'sage.rings.finite_rings.element_givaro.FiniteField_givaroElement'>) to Rational
The base ring for this simplicial complex.
EXAMPLES:
sage: ChainComplex().base_ring()
Integer Ring
The Betti number of the homology of the chain complex in this dimension.
That is, write the homology in this dimension as a direct sum of a free module and a torsion module; the Betti number is the rank of the free summand.
INPUT:
OUTPUT: the Betti number in dimension dim - the rank of the free part of the homology module in this dimension.
EXAMPLES:
sage: C = ChainComplex({0: matrix(ZZ, 2, 3, [3, 0, 0, 0, 0, 0])})
sage: C.betti(0)
2
sage: [C.betti(n) for n in range(5)]
[2, 1, 0, 0, 0]
sage: C.betti()
{0: 2, 1: 1}
Return the category to which this chain complex belongs: the category of all chain complexes over the base ring.
EXAMPLES:
sage: C = ChainComplex({0: matrix(ZZ, 2, 3, [3, 0, 0, 0, 0, 0])}, base_ring=GF(7))
sage: C.category()
Category of chain complexes over Finite Field of size 7
The differentials which make up the chain complex.
INPUT:
OUTPUT: either a dictionary of all of the differentials or a single differential (i.e., a matrix)
EXAMPLES:
sage: D = ChainComplex({0: matrix(ZZ, 2, 2, [1,0,0,2])})
sage: D.differential()
{0: [1 0]
[0 2], 1: []}
sage: D.differential(0)
[1 0]
[0 2]
sage: C = ChainComplex({0: identity_matrix(ZZ, 40)})
sage: C.differential()
{0: 40 x 40 dense matrix over Integer Ring, 1: []}
The dual chain complex to self.
Since all modules in self are free of finite rank, the
dual in dimension  is isomorphic to the original chain
complex in dimension
is isomorphic to the original chain
complex in dimension  , and the corresponding boundary
matrix is the transpose of the matrix in the original complex.
This converts a chain complex to a cochain complex and vice
versa.
, and the corresponding boundary
matrix is the transpose of the matrix in the original complex.
This converts a chain complex to a cochain complex and vice
versa.
EXAMPLES:
sage: C = ChainComplex({2: matrix(ZZ, 2, 3, [3, 0, 0, 0, 0, 0])})
sage: C._degree
1
sage: C.differential(2)
[3 0 0]
[0 0 0]
sage: C.dual()._degree
-1
sage: C.dual().differential(3)
[3 0]
[0 0]
[0 0]
The free module underlying this chain complex.
EXAMPLES:
sage: C = ChainComplex({0: matrix(ZZ, 2, 3, [3, 0, 0, 0, 0, 0]), 1: matrix(ZZ, 0, 2)})
sage: C.free_module()
Ambient free module of rank 5 over the principal ideal domain Integer Ring
This defines the forgetful functor from the category of chain complexes to the category of free modules:
sage: FreeModules(ZZ)(C)
Ambient free module of rank 5 over the principal ideal domain Integer Ring
The homology of the chain complex in the given dimension.
INPUT:
 or a field.
or a field.OUTPUT: if dim is specified, the homology in dimension dim. Otherwise, the homology in every dimension as a dictionary indexed by dimension.
ALGORITHM:
If algorithm is set to ‘auto’ (the default), then use CHomP if available. (CHomP is available at the web page http://chomp.rutgers.edu/. It is also an experimental package for Sage.)
CHomP computes homology, not cohomology, and only works over the integers or finite prime fields. Therefore if any of these conditions fails, or if CHomP is not present, or if algorithm is set to ‘no_chomp’, go to plan B: if self has a _homology method – each simplicial complex has this, for example – then call that. Such a method implements specialized algorithms for the particular type of cell complex.
Otherwise, move on to plan C: compute the chain complex of self and compute its homology groups. To do this: over a field, just compute ranks and nullities, thus obtaining dimensions of the homology groups as vector spaces. Over the integers, compute Smith normal form of the boundary matrices defining the chain complex according to the value of algorithm. If algorithm is ‘auto’ or ‘no_chomp’, then for each relatively small matrix, use the standard Sage method, which calls the Pari package. For any large matrix, reduce it using the Dumas, Heckenbach, Saunders, and Welker elimination algorithm: see sage.homology.chain_complex.dhsw_snf() for details.
Finally, algorithm may also be ‘pari’ or ‘dhsw’, which forces the named algorithm to be used regardless of the size of the matrices and regardless of whether CHomP is available.
As of this writing, CHomP is by far the fastest option, followed by the ‘auto’ or ‘no_chomp’ setting of using the Dumas, Heckenbach, Saunders, and Welker elimination algorithm for large matrices and Pari for small ones.
Warning
This only works if the base ring is the integers or a field. Other values will return an error.
EXAMPLES:
sage: C = ChainComplex({0: matrix(ZZ, 2, 3, [3, 0, 0, 0, 0, 0])})
sage: C.homology()
{0: Z x Z, 1: Z x C3}
sage: C.homology(dim=1, base_ring = GF(3))
Vector space of dimension 2 over Finite Field of size 3
sage: D = ChainComplex({0: identity_matrix(ZZ, 4), 4: identity_matrix(ZZ, 30)})
sage: D.homology()
{0: 0, 1: 0, 4: 0, 5: 0}
Generators (only available via CHomP): generators are given as a list of cycles, each of which is an element in the appropriate free module, and hence is represented as a vector:
sage: C.homology(1, generators=True) # optional: need CHomP
(Z x C3, [(1, 0), (0, 1)])
Look for torsion in this chain complex by computing its mod  homology for a range of primes
homology for a range of primes  .
.
INPUT:
 for
all
for
all  strictly less than this number.
strictly less than this number. for primes at least as big as this.
for primes at least as big as this.Return a list of pairs ( , dims) where
, dims) where  is a prime at
which there is torsion and dims is a list of dimensions in
which this torsion occurs.
is a prime at
which there is torsion and dims is a list of dimensions in
which this torsion occurs.
The base ring for the chain complex must be the integers; if not, an error is raised.
Algorithm: let 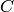 denote the chain complex. Let
denote the chain complex. Let 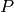 equal
max_prime. Compute the mod
equal
max_prime. Compute the mod 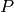 homology of
homology of 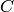 , and use
this as the base-line computation: the assumption is that this
is isomorphic to the integral homology tensored with
, and use
this as the base-line computation: the assumption is that this
is isomorphic to the integral homology tensored with
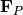 . Then compute the mod
. Then compute the mod  homology for a range of
primes
homology for a range of
primes  , and record whenever the answer differs from the
base-line answer.
, and record whenever the answer differs from the
base-line answer.
EXAMPLES:
sage: C = ChainComplex({0: matrix(ZZ, 2, 3, [3, 0, 0, 0, 0, 0])})
sage: C.homology()
{0: Z x Z, 1: Z x C3}
sage: C.torsion_list(11)
[(3, [1])]
sage: C = ChainComplex([matrix(ZZ, 1, 1, [2]), matrix(ZZ, 1, 1), matrix(1, 1, [3])])
sage: C.homology(1)
C2
sage: C.homology(3)
C3
sage: C.torsion_list(5)
[(2, [1]), (3, [3])]
Abelian group on  generators. This class inherits from
AbelianGroup; see that for more documentation. The main
difference between the classes is in the print representation;
also, this class does not accept a names argument.
generators. This class inherits from
AbelianGroup; see that for more documentation. The main
difference between the classes is in the print representation;
also, this class does not accept a names argument.
EXAMPLES:
sage: from sage.homology.chain_complex import HomologyGroup
sage: G = AbelianGroup(5,[5,5,7,8,9]); G
Multiplicative Abelian Group isomorphic to C5 x C5 x C7 x C8 x C9
sage: H = HomologyGroup(5,[5,5,7,8,9]); H
C5 x C5 x C7 x C8 x C9
sage: AbelianGroup(4)
Multiplicative Abelian Group isomorphic to Z x Z x Z x Z
sage: HomologyGroup(4)
Z x Z x Z x Z
sage: HomologyGroup(100)
Z^100
Bases: sage.groups.abelian_gps.abelian_group.AbelianGroup_class
Abelian group on  generators. This class inherits from
AbelianGroup; see that for more documentation. The main
difference between the classes is in the print representation;
also, this class does not accept a names argument.
generators. This class inherits from
AbelianGroup; see that for more documentation. The main
difference between the classes is in the print representation;
also, this class does not accept a names argument.
EXAMPLES:
sage: from sage.homology.chain_complex import HomologyGroup
sage: G = AbelianGroup(5,[5,5,7,8,9]); G
Multiplicative Abelian Group isomorphic to C5 x C5 x C7 x C8 x C9
sage: H = HomologyGroup(5,[5,5,7,8,9]); H
C5 x C5 x C7 x C8 x C9
sage: G == loads(dumps(G))
True
sage: AbelianGroup(4)
Multiplicative Abelian Group isomorphic to Z x Z x Z x Z
sage: HomologyGroup(4)
Z x Z x Z x Z
sage: HomologyGroup(100)
Z^100
Preprocess a matrix using the “Elimination algorithm” described by Dumas et al., and then call elementary_divisors on the resulting (smaller) matrix.
‘dhsw’ stands for ‘Dumas, Heckenbach, Saunders, Welker,’ and ‘snf’ stands for ‘Smith Normal Form.’
INPUT:
(They use the transpose of the matrix considered here, so they use rows instead of columns.)
Algorithm: go through mat one column at a time. For each column, add multiples of previous columns to it until either
- it’s zero, in which case it should be deleted.
- its first nonzero entry is 1 or -1, in which case it should be kept.
- its first nonzero entry is something else, in which case it is deferred until the second pass.
Then do a second pass on the deferred columns.
At this point, the columns with 1 or -1 in the first entry
contribute to the rank of the matrix, and these can be counted and
then deleted (after using the 1 or -1 entry to clear out its row).
Suppose that there were  of these.
of these.
The resulting matrix should be much smaller; we then feed it
to Sage’s elementary_divisors function, and prepend  1’s to
account for the rows deleted in the previous step.
1’s to
account for the rows deleted in the previous step.
EXAMPLES:
sage: from sage.homology.chain_complex import dhsw_snf
sage: mat = matrix(ZZ, 3, 4, range(12))
sage: dhsw_snf(mat)
[1, 4, 0]
sage: mat = random_matrix(ZZ, 20, 20, x=-1, y=2)
sage: mat.elementary_divisors() == dhsw_snf(mat)
True
REFERENCES: