A collection of functions implementing generic algorithms in arbitrary groups, including additive and multiplicative groups.
In all cases the group operation is specified by a parameter ‘operation’, which is a string either one of the set of multiplication_names or addition_names specified below, or ‘other’. In the latter case, the caller must provide an identity, inverse() and op() functions.
multiplication_names = ( 'multiplication', 'times', 'product', '*')
addition_names = ( 'addition', 'plus', 'sum', '+')
Also included are a generic function for computing multiples (or powers), and an iterator for general multiples and powers.
EXAMPLES:
Some examples in the multiplicative group of a finite field:
Discrete logs:
sage: K = GF(3^6,'b')
sage: b = K.gen()
sage: a = b^210
sage: discrete_log(a, b, K.order()-1)
210
Linear relation finder:
sage: F.<a>=GF(3^6,'a')
sage: a.multiplicative_order().factor()
2^3 * 7 * 13
sage: b=a^7
sage: c=a^13
sage: linear_relation(b,c,'*')
(13, 7)
sage: b^13==c^7
True
Orders of elements:
sage: k.<a> = GF(5^5)
sage: b = a^4
sage: order_from_multiple(b,5^5-1,operation='*')
781
sage: order_from_bounds(b,(5^4,5^5),operation='*')
781
Some examples in the group of points of an elliptic curve over a finite field:
Discrete logs:
sage: F=GF(37^2,'a')
sage: E=EllipticCurve(F,[1,1])
sage: F.<a>=GF(37^2,'a')
sage: E=EllipticCurve(F,[1,1])
sage: P=E(25*a + 16 , 15*a + 7 )
sage: P.order()
672
sage: Q=39*P; Q
(36*a + 32 : 5*a + 12 : 1)
sage: discrete_log(Q,P,P.order(),operation='+')
39
Linear relation finder:
sage: F.<a>=GF(3^6,'a')
sage: E=EllipticCurve([a^5 + 2*a^3 + 2*a^2 + 2*a, a^4 + a^3 + 2*a + 1])
sage: P=E(a^5 + a^4 + a^3 + a^2 + a + 2 , 0)
sage: Q=E(2*a^3 + 2*a^2 + 2*a , a^3 + 2*a^2 + 1)
sage: linear_relation(P,Q,'+')
(1, 2)
sage: P == 2*Q
True
Orders of elements:
sage: k.<a> = GF(5^5)
sage: E = EllipticCurve(k,[2,4])
sage: P = E(3*a^4 + 3*a , 2*a + 1 )
sage: M = E.cardinality(); M
3227
sage: plist = M.prime_factors()
sage: order_from_multiple(P, M, plist, operation='+')
3227
sage: Q = E(0,2)
sage: order_from_multiple(Q, M, plist, operation='+')
7
sage: order_from_bounds(Q, Hasse_bounds(5^5), operation='+')
7
Totally generic discrete baby-step giant-step function.
Solves 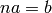 (or
(or 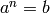 ) with
) with 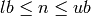 where bounds==(lb,ub),
raising an error if no such
where bounds==(lb,ub),
raising an error if no such  exists.
exists.
 and
and  must be elements of some group with given identity,
inverse of x given by inverse(x), and group operation on
x, y by op(x,y).
must be elements of some group with given identity,
inverse of x given by inverse(x), and group operation on
x, y by op(x,y).
If operation is ‘*’ or ‘+’ then the other arguments are provided automatically; otherwise they must be provided by the caller.
INPUT:
OUTPUT:
An integer  such that
such that 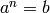 (or
(or 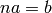 ). If no
such
). If no
such  exists, this function raises a ValueError exception.
exists, this function raises a ValueError exception.
NOTE: This is a generalization of discrete logarithm. One situation where this version is useful is to find the order of an element in a group where we only have bounds on the group order (see the elliptic curve example below).
ALGORITHM: Baby step giant step. Time and space are soft
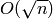 where
where  is the difference between upper and lower
bounds.
is the difference between upper and lower
bounds.
EXAMPLES:
sage: b = Mod(2,37); a = b^20
sage: bsgs(b, a, (0,36))
20
sage: p=next_prime(10^20)
sage: a=Mod(2,p); b=a^(10^25)
sage: bsgs(a, b, (10^25-10^6,10^25+10^6)) == 10^25
True
sage: K = GF(3^6,'b')
sage: a = K.gen()
sage: b = a^210
sage: bsgs(a, b, (0,K.order()-1))
210
sage: K.<z>=CyclotomicField(230)
sage: w=z^500
sage: bsgs(z,w,(0,229))
40
An additive example in an elliptic curve group:
sage: F.<a>=GF(37^5,'a')
sage: E=EllipticCurve(F,[1,1])
sage: P=E.lift_x(a); P
(a : 9*a^4 + 22*a^3 + 23*a^2 + 30 : 1)
This will return a multiple of the order of P:
sage: bsgs(P,P.parent()(0),Hasse_bounds(F.order()),operation='+')
69327408
AUTHOR:
- John Cremona (2008-03-15)
Totally generic discrete log function.
INPUT:
a and base must be elements of some group with identity given by identity, inverse of x by inverse(x), and group operation on x, y by op(x,y).
If operation is ‘*’ or ‘+’ then the other arguments are provided automatically; otherwise they must be provided by the caller.
OUTPUT: Returns an integer  such that
such that 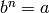 (or
(or 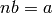 ),
assuming that ord is a multiple of the order of the base
),
assuming that ord is a multiple of the order of the base  .
If ord is not specified, an attempt is made to compute it.
.
If ord is not specified, an attempt is made to compute it.
If no such  exists, this function raises a ValueError exception.
exists, this function raises a ValueError exception.
Warning
If x has a log method, it is likely to be vastly faster
than using this function. E.g., if x is an integer modulo
 , use its log method instead!
, use its log method instead!
ALGORITHM: Pohlig-Hellman and Baby step giant step.
EXAMPLES:
sage: b = Mod(2,37); a = b^20
sage: discrete_log(a, b)
20
sage: b = Mod(2,997); a = b^20
sage: discrete_log(a, b)
20
sage: K = GF(3^6,'b')
sage: b = K.gen()
sage: a = b^210
sage: discrete_log(a, b, K.order()-1)
210
sage: b = Mod(1,37); x = Mod(2,37)
sage: discrete_log(x, b)
...
ValueError: No discrete log of 2 found to base 1
sage: b = Mod(1,997); x = Mod(2,997)
sage: discrete_log(x, b)
...
ValueError: No discrete log of 2 found to base 1
See trac\#2356:
sage: F.<w> = GF(121)
sage: v = w^120
sage: v.log(w)
0
sage: K.<z>=CyclotomicField(230)
sage: w=z^50
sage: discrete_log(w,z)
50
An example where the order is infinite: note that we must give an upper bound here:
sage: K.<a> = QuadraticField(23)
sage: eps = 5*a-24 # a fundamental unit
sage: eps.multiplicative_order()
+Infinity
sage: eta = eps^100
sage: discrete_log(eta,eps,bounds=(0,1000))
100
In this case we cannot detect negative powers:
sage: eta = eps^(-3)
sage: discrete_log(eta,eps,bounds=(0,100))
...
ValueError: No discrete log of -11515*a - 55224 found to base 5*a - 24
But we can invert the base (and negate the result) instead:
sage: - discrete_log(eta^-1,eps,bounds=(0,100))
-3
An additive example: elliptic curve DLOG:
sage: F=GF(37^2,'a')
sage: E=EllipticCurve(F,[1,1])
sage: F.<a>=GF(37^2,'a')
sage: E=EllipticCurve(F,[1,1])
sage: P=E(25*a + 16 , 15*a + 7 )
sage: P.order()
672
sage: Q=39*P; Q
(36*a + 32 : 5*a + 12 : 1)
sage: discrete_log(Q,P,P.order(),operation='+')
39
An example of big smooth group:
sage: F.<a>=GF(2^63)
sage: g=F.gen()
sage: u=g**123456789
sage: discrete_log(u,g)
123456789
AUTHORS:
Pollard Lambda algorithm for computing discrete logarithms. It uses only a logarithmic amount of memory. It’s useful if you have bounds on the logarithm. If you are computing logarithms in a whole finite group, you should use Pollard Rho algorithm. INPUT:
OUTPUT: Returns an integer  such that
such that 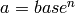 (or
(or 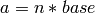 )
)
EXEMPLES:
sage: F.<a> = GF(2^63)
sage: discrete_log_lambda(a^1234567, a, (1200000,1250000))
1234567
sage: F.<a> = GF(37^5, 'a')
sage: E = EllipticCurve(F, [1,1])
sage: P=E.lift_x(a); P
(a : 9*a^4 + 22*a^3 + 23*a^2 + 30 : 1)
This will return a multiple of the order of P:
sage: discrete_log_lambda(P.parent()(0), P, Hasse_bounds(F.order()), operation='+')
69327408
sage: K.<a> = GF(89**5)
sage: hs = lambda x: hash(x) + 15
sage: discrete_log_lambda(a**(89**3 - 3), a, (89**2, 89**4), operation = '*', hash_function = hs)
704966
Pollard Rho algorithm for computing discrete logarithm in cyclic group of prime order. If the group order is very small it falls back to the baby step giant step algorithm.
INPUT:
a - a group element
base - a group element
ord - the order of base or None, in this case we try to compute it
additive group or a multiplicative one
for this algorithm (see examples)
OUTPUT: return an integer  such that
such that 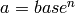 (or
(or 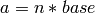 )
)
ALGORITHM: Pollard rho for discrete logarithm, adapted from the article of Edlyn Teske, ‘A space efficient algorithm for group structure computation’
EXAMPLES:
sage: F.<a> = GF(2^13)
sage: g = F.gen()
sage: discrete_log_rho(g^1234, g)
1234
sage: F.<a> = GF(37^5, 'a')
sage: E = EllipticCurve(F, [1,1])
sage: G = 3*31*2^4*E.lift_x(a)
sage: discrete_log_rho(12345*G, G, ord=46591, operation='+')
12345
It also works with matrices:
sage: A = matrix(GF(50021),[[10577,23999,28893],[14601,41019,30188],[3081,736,27092]])
sage: discrete_log_rho(A^1234567, A)
1234567
Beware, the order must be prime:
sage: I = IntegerModRing(171980)
sage: discrete_log_rho(I(2), I(3))
...
ValueError: for Pollard rho algorithm the order of the group must be prime
If it fails to find a suitable logarithm, it raises a ValueError:
sage: I = IntegerModRing(171980)
sage: discrete_log_rho(I(31002),I(15501))
...
ValueError: Pollard rho algorithm failed to find a logarithm
The main limitation on the hash function is that we don’t want to have
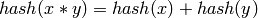 :
:
sage: I = IntegerModRing(next_prime(2^23))
sage: def test():
... try:
... discrete_log_rho(I(123456),I(1),operation='+')
... except:
... print "FAILURE"
sage: test() # random failure
FAILURE
If this happens, we can provide a better hash function:
sage: discrete_log_rho(I(123456),I(1),operation='+', hash_function=lambda x: hash(x*x))
123456
AUTHOR:
Function which solves the equation a*P=m*Q or P^a=Q^m.
Additive version: returns 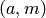 with minimal
with minimal 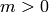 such that
such that
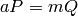 . Special case: if
. Special case: if 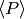 and
and 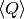 intersect only in
intersect only in 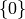 then
then 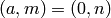 where
where  is
Q.additive_order().
is
Q.additive_order().
Multiplicative version: returns 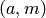 with minimal
with minimal 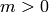 such
that
such
that 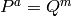 . Special case: if
. Special case: if 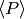 and
and
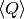 intersect only in
intersect only in 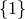 then
then 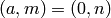 where
where  is Q.multiplicative_order().
is Q.multiplicative_order().
ALGORITHM:
Uses the generic bsgs() function, and so works in general finite abelian groups.
EXAMPLES:
An additive example (in an elliptic curve group):
sage: F.<a>=GF(3^6,'a')
sage: E=EllipticCurve([a^5 + 2*a^3 + 2*a^2 + 2*a, a^4 + a^3 + 2*a + 1])
sage: P=E(a^5 + a^4 + a^3 + a^2 + a + 2 , 0)
sage: Q=E(2*a^3 + 2*a^2 + 2*a , a^3 + 2*a^2 + 1)
sage: linear_relation(P,Q,'+')
(1, 2)
sage: P == 2*Q
True
A multiplicative example (in a finite field’s multiplicative group):
sage: F.<a>=GF(3^6,'a')
sage: a.multiplicative_order().factor()
2^3 * 7 * 13
sage: b=a^7
sage: c=a^13
sage: linear_relation(b,c,'*')
(13, 7)
sage: b^13==c^7
True
Returns a group element whose order is the lcm of the given elements.
INPUT:
P1 – a pair 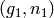 where
where 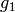 is a group element of order
is a group element of order 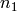
P2 – a pair 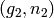 where
where 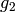 is a group element of order
is a group element of order 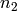
operation – string: ‘+’ (default ) or ‘*’ or other. If other, the following must be supplied:
identity: the identity element for the group;
inverse(): a function of one argument giving the inverse of a group element;
- op(): a function of 2 arguments defining the group
binary operation.
OUTPUT:
A pair 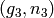 where
where 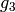 has order
has order 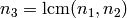 .
.
EXAMPLES:
sage: F.<a>=GF(3^6,'a')
sage: b = a^7
sage: c = a^13
sage: ob = (3^6-1)//7
sage: oc = (3^6-1)//13
sage: merge_points((b,ob),(c,oc),operation='*')
(a^4 + 2*a^3 + 2*a^2, 728)
sage: d,od = merge_points((b,ob),(c,oc),operation='*')
sage: od == d.multiplicative_order()
True
sage: od == lcm(ob,oc)
True
sage: E=EllipticCurve([a^5 + 2*a^3 + 2*a^2 + 2*a, a^4 + a^3 + 2*a + 1])
sage: P=E(2*a^5 + 2*a^4 + a^3 + 2 , a^4 + a^3 + a^2 + 2*a + 2)
sage: P.order()
7
sage: Q=E(2*a^5 + 2*a^4 + 1 , a^5 + 2*a^3 + 2*a + 2 )
sage: Q.order()
4
sage: R,m = merge_points((P,7),(Q,4), operation='+')
sage: R.order() == m
True
sage: m == lcm(7,4)
True
Returns either 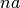 or
or 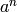 , where
, where  is any integer and
is any integer and  is
a Python object on which a group operation such as addition or
multiplication is defined. Uses the standard binary algorithm.
is
a Python object on which a group operation such as addition or
multiplication is defined. Uses the standard binary algorithm.
INPUT: See the documentation for discrete_logarithm().
EXAMPLES:
sage: multiple(2,5)
32
sage: multiple(RealField()('2.5'),4)
39.0625000000000
sage: multiple(2,-3)
1/8
sage: multiple(2,100,'+') == 100*2
True
sage: multiple(2,100) == 2**100
True
sage: multiple(2,-100,) == 2**-100
True
sage: R.<x>=ZZ[]
sage: multiple(x,100)
x^100
sage: multiple(x,100,'+')
100*x
sage: multiple(x,-10)
1/x^10
Idempotence is detected, making the following fast:
sage: multiple(1,10^1000)
1
sage: E=EllipticCurve('389a1')
sage: P=E(-1,1)
sage: multiple(P,10,'+')
(645656132358737542773209599489/22817025904944891235367494656 : 525532176124281192881231818644174845702936831/3446581505217248068297884384990762467229696 : 1)
sage: multiple(P,-10,'+')
(645656132358737542773209599489/22817025904944891235367494656 : -528978757629498440949529703029165608170166527/3446581505217248068297884384990762467229696 : 1)
Return an iterator which runs through P0+i*P for i in range(n).
P and P0 must be Sage objects in some group; if the operation is multiplication then the returned values are instead P0*P**i.
EXAMPLES:
sage: list(multiples(1,10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
sage: list(multiples(1,10,100))
[100, 101, 102, 103, 104, 105, 106, 107, 108, 109]
sage: E=EllipticCurve('389a1')
sage: P=E(-1,1)
sage: for Q in multiples(P,5): print Q, Q.height()/P.height()
(0 : 1 : 0) 0.000000000000000
(-1 : 1 : 1) 1.00000000000000
(10/9 : -35/27 : 1) 4.00000000000000
(26/361 : -5720/6859 : 1) 9.00000000000000
(47503/16641 : 9862190/2146689 : 1) 16.0000000000000
sage: R.<x>=ZZ[]
sage: list(multiples(x,5))
[0, x, 2*x, 3*x, 4*x]
sage: list(multiples(x,5,operation='*'))
[1, x, x^2, x^3, x^4]
sage: list(multiples(x,5,indexed=True))
[(0, 0), (1, x), (2, 2*x), (3, 3*x), (4, 4*x)]
sage: list(multiples(x,5,indexed=True,operation='*'))
[(0, 1), (1, x), (2, x^2), (3, x^3), (4, x^4)]
sage: for i,y in multiples(x,5,indexed=True): print "%s times %s = %s"%(i,x,y)
0 times x = 0
1 times x = x
2 times x = 2*x
3 times x = 3*x
4 times x = 4*x
sage: for i,n in multiples(3,5,indexed=True,operation='*'): print "3 to the power %s = %s"%(i,n)
3 to the power 0 = 1
3 to the power 1 = 3
3 to the power 2 = 9
3 to the power 3 = 27
3 to the power 4 = 81
Generic function to find order of a group element, given only upper and lower bounds for a multiple of the order (e.g. bounds on the order of the group of which it is an element)
INPUT:
Note
Typically lb and ub will be bounds on the group order, and from previous calculation we know that the group order is divisible by d.
EXAMPLES:
sage: k.<a> = GF(5^5)
sage: b = a^4
sage: order_from_bounds(b,(5^4,5^5),operation='*')
781
sage: E = EllipticCurve(k,[2,4])
sage: P = E(3*a^4 + 3*a , 2*a + 1 )
sage: bounds = Hasse_bounds(5^5)
sage: Q = E(0,2)
sage: order_from_bounds(Q, bounds, operation='+')
7
sage: order_from_bounds(P, bounds, 7, operation='+')
3227
sage: K.<z>=CyclotomicField(230)
sage: w=z^50
sage: order_from_bounds(w,(200,250),operation='*')
23
Generic function to find order of a group element given a multiple of its order.
INPUT:
Note
It is more efficient for the caller to factor m and cache the factors for subsequent calls.
EXAMPLES:
sage: k.<a> = GF(5^5)
sage: b = a^4
sage: order_from_multiple(b,5^5-1,operation='*')
781
sage: E = EllipticCurve(k,[2,4])
sage: P = E(3*a^4 + 3*a , 2*a + 1 )
sage: M = E.cardinality(); M
3227
sage: F = M.factor()
sage: order_from_multiple(P, M, factorization=F, operation='+')
3227
sage: Q = E(0,2)
sage: order_from_multiple(Q, M, factorization=F, operation='+')
7
sage: K.<z>=CyclotomicField(230)
sage: w=z^50
sage: order_from_multiple(w,230,operation='*')
23
sage: F=GF(2^1279,'a')
sage: n=F.cardinality()-1 # Mersenne prime
sage: order_from_multiple(F.random_element(),n,factorization=[(n,1)],operation='*')==n
True
sage: K.<a> = GF(3^60)
sage: order_from_multiple(a, 3^60-1, operation='*', check=False)
42391158275216203514294433200