Bases: sage.symbolic.function.BuiltinFunction
Dickman’s function is the continuous function satisfying the differential equation
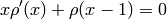
with initial conditions 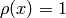 for
for
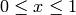 . It is useful in estimating the frequency
of smooth numbers as asymptotically
. It is useful in estimating the frequency
of smooth numbers as asymptotically
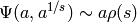
where 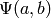 is the number of
is the number of 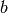 -smooth
numbers less than
-smooth
numbers less than  .
.
ALGORITHM:
Dickmans’s function is analytic on the interval
![[n,n+1]](../../_images/math/f6c8b16b270bb48ba00cc1bd78df9bb594647c73.png) for each integer
for each integer  . To evaluate at
. To evaluate at
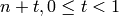 , a power series is recursively computed
about
, a power series is recursively computed
about 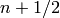 using the differential equation stated above.
As high precision arithmetic may be needed for intermediate results
the computed series are cached for later use.
using the differential equation stated above.
As high precision arithmetic may be needed for intermediate results
the computed series are cached for later use.
Simple explicit formulas are used for the intervals [0,1] and [1,2].
EXAMPLES:
sage: dickman_rho(2)
0.306852819440055
sage: dickman_rho(10)
2.77017183772596e-11
sage: dickman_rho(10.00000000000000000000000000000000000000)
2.77017183772595898875812120063434232634e-11
sage: plot(log(dickman_rho(x)), (x, 0, 15))
AUTHORS:
REFERENCES:
Approximate using de Bruijn’s formula
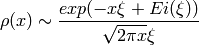
which is asymptotically equal to Dickman’s function, and is much faster to compute.
REFERENCES:
EXAMPLES:
sage: dickman_rho.approximate(10)
2.41739196365564e-11
sage: dickman_rho(10)
2.77017183772596e-11
sage: dickman_rho.approximate(1000)
4.32938809066403e-3464
This function returns the power series about 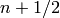 used
to evaluate Dickman’s function. It is scaled such that the interval
used
to evaluate Dickman’s function. It is scaled such that the interval
![[n,n+1]](../../_images/math/f6c8b16b270bb48ba00cc1bd78df9bb594647c73.png) corresponds to x in
corresponds to x in ![[-1,1]](../../_images/math/39f506ebeeeb72f62147990614a67f4e30b7c751.png) .
.
INPUT:
EXAMPLES:
sage: f = dickman_rho.power_series(2, 20); f
-9.9376e-8*x^11 + 3.7722e-7*x^10 - 1.4684e-6*x^9 + 5.8783e-6*x^8 - 0.000024259*x^7 + 0.00010341*x^6 - 0.00045583*x^5 + 0.0020773*x^4 - 0.0097336*x^3 + 0.045224*x^2 - 0.11891*x + 0.13032
sage: f(-1), f(0), f(1)
(0.30685, 0.13032, 0.048608)
sage: dickman_rho(2), dickman_rho(2.5), dickman_rho(3)
(0.306852819440055, 0.130319561832251, 0.0486083882911316)
Return value of the function Li(x) as a real double field element.
This is the function
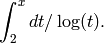
The function Li(x) is an approximation for the number of primes up
to 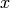 . In fact, the famous Riemann Hypothesis is
equivalent to the statement that for
. In fact, the famous Riemann Hypothesis is
equivalent to the statement that for 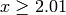 we have
we have
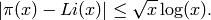
For “small” 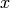 ,
, 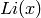 is always slightly bigger
than
is always slightly bigger
than 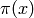 . However it is a theorem that there are (very
large, e.g., around
. However it is a theorem that there are (very
large, e.g., around 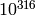 ) values of
) values of 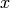 so
that
so
that 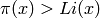 . See
“A new bound for the smallest x with
. See
“A new bound for the smallest x with 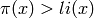 “,
Bays and Hudson, Mathematics of Computation, 69 (2000) 1285-1296.
“,
Bays and Hudson, Mathematics of Computation, 69 (2000) 1285-1296.
ALGORITHM: Computed numerically using GSL.
INPUT:
OUTPUT:
EXAMPLES:
sage: Li(2)
0.0
sage: Li(5)
2.58942452992
sage: Li(1000)
176.56449421
sage: Li(10^5)
9628.76383727
sage: prime_pi(10^5)
9592
sage: Li(1)
...
ValueError: Li only defined for x at least 2.
sage: for n in range(1,7):
... print '%-10s%-10s%-20s'%(10^n, prime_pi(10^n), Li(10^n))
10 4 5.12043572467
100 25 29.080977804
1000 168 176.56449421
10000 1229 1245.09205212
100000 9592 9628.76383727
1000000 78498 78626.5039957
Returns the exponential integral 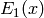 . If the optional
argument
. If the optional
argument  is given, computes list of the first
is given, computes list of the first
 values of the exponential integral
values of the exponential integral
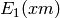 .
.
The exponential integral 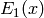 is
is
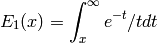
INPUT:
OUTPUT:
EXAMPLES:
sage: exponential_integral_1(2)
0.048900510708061118
sage: w = exponential_integral_1(2,4); w
[0.048900510708061118, 0.0037793524098489067, 0.00036008245216265873, 3.7665622843924751e-05] # 32-bit
[0.048900510708061118, 0.0037793524098489063, 0.00036008245216265873, 3.7665622843924534e-05] # 64-bit
IMPLEMENTATION: We use the PARI C-library functions eint1 and veceint1.
REFERENCE:
REMARKS: When called with the optional argument n, the PARI C-library is fast for values of n up to some bound, then very very slow. For example, if x=5, then the computation takes less than a second for n=800000, and takes “forever” for n=900000.
Completed function 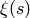 that satisfies
that satisfies
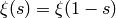 and has zeros at the same points as the
Riemann zeta function.
and has zeros at the same points as the
Riemann zeta function.
INPUT:
If s is a real number the computation is done using the MPFR library. When the input is not real, the computation is done using the PARI C library.
More precisely,
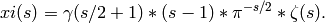
EXAMPLES:
sage: zeta_symmetric(0.7)
0.497580414651127
sage: zeta_symmetric(1-0.7)
0.497580414651127
sage: RR = RealField(200)
sage: zeta_symmetric(RR(0.7))
0.49758041465112690357779107525638385212657443284080589766062
sage: C.<i> = ComplexField()
sage: zeta_symmetric(0.5 + i*14.0)
0.000201294444235258 + 1.49077798716757e-19*I
sage: zeta_symmetric(0.5 + i*14.1)
0.0000489893483255687 + 4.40457132572236e-20*I
sage: zeta_symmetric(0.5 + i*14.2)
-0.0000868931282620101 + 7.11507675693612e-20*I
REFERENCE: