Counting Primes

AUTHORS:

• 18. Andrew Ohana
• William Stein

TESTS:

sage: z = sage.functions.prime_pi.PrimePi()
sage: loads(dumps(z))
Function that counts the number of primes up to x
sage: loads(dumps(z)) == z
True

class sage.functions.prime_pi.PrimePi

Bases: object

Return the number of primes .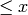

EXAMPLES:

sage: prime_pi(7)
4
sage: prime_pi(100)
25
sage: prime_pi(1000)
168
sage: prime_pi(100000)
9592
sage: prime_pi(0.5)
0
sage: prime_pi(-10)
0
sage: prime_pi(500509)
41581

The following test is to verify that ticket #4670 has been essentially resolved:

sage: prime_pi(10**10)
455052511

The prime_pi function allows for use of additional memory:

sage: prime_pi(500509, 8)
41581

The prime_pi function also has a special plotting method, so it plots quickly and perfectly as a step function:

sage: P = plot(prime_pi, 50,100)

plot(xmin, xmax=0, vertical_lines=100, **kwds=True)

Draw a plot of the prime counting function from xmin to xmax. All additional arguments are passed on to the line command.

WARNING: we draw the plot of prime_pi as a stairstep function with explicitly drawn vertical lines where the function jumps. Technically there should not be any vertical lines, but they make the graph look much better, so we include them. Use the option vertical_lines=False to turn these off.

EXAMPLES:

sage: plot(prime_pi, 1, 100)
sage: prime_pi.plot(-2,50,thickness=2, vertical_lines=False)