Sage gives access to the Stein-Watkins table of elliptic curves, via an optional package that you must install. This is a huge database of elliptic curves. You can download the database as a 2.6GB Sage package from http://modular.ucsd.edu/sagedb/, which you install with the command
sage -i stein-watkins-ecdb.spkg
You can also download a small version, without having to explicitly download anything from a website, using the command
sage -i stein-watkins-ecdb-mini
This database covers a wide range of conductors, but unlike CremonaDatabase(), this database need not list all curves of a given conductor. It lists the curves whose coefficients aren’t “too large” (see [Stein-Watkins, Ants 5]).
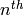 Stein-Watkins table,
which contains elliptic curves of conductor between
Stein-Watkins table,
which contains elliptic curves of conductor between 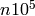 and
and 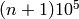 . Here
. Here  can be between
can be between
 and
and 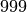 , inclusive.
, inclusive.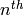 Stein-Watkins table,
which contains prime conductor elliptic curves of conductor between
Stein-Watkins table,
which contains prime conductor elliptic curves of conductor between
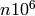 and
and 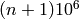 . Here
. Here  varies
between
varies
between  and
and 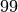 , inclusive.
, inclusive.EXAMPLES: We obtain the first table of elliptic curves.
sage: d = SteinWatkinsAllData(0)
sage: d
Stein-Watkins Database a.0 Iterator
We type d.next() to get each isogeny class of curves from d:
sage: C = d.next() # optional - stein_watkins_database
sage: C # optional - stein_watkins_database
Stein-Watkins isogeny class of conductor 11
sage: d.next() # optional - stein_watkins_database
Stein-Watkins isogeny class of conductor 14
sage: d.next() # optional - stein_watkins_database
Stein-Watkins isogeny class of conductor 15
An isogeny class has a number of attributes that give data about
the isogeny class, such as the rank, equations of curves,
conductor, leading coefficient of  -function, etc.
-function, etc.
sage: C.data # optional - stein_watkins_database
['11', '[11]', '0', '0.253842', '25', '+*1']
sage: C.curves # optional - stein_watkins_database
[[[0, -1, 1, 0, 0], '(1)', '1', '5'],
[[0, -1, 1, -10, -20], '(5)', '1', '5'],
[[0, -1, 1, -7820, -263580], '(1)', '1', '1']]
sage: C.conductor # optional - stein_watkins_database
11
sage: C.leading_coefficient # optional - stein_watkins_database
'0.253842'
sage: C.modular_degree # optional - stein_watkins_database
'+*1'
sage: C.rank # optional - stein_watkins_database
0
sage: C.isogeny_number # optional - stein_watkins_database
'25'
If we were to continue typing d.next() we would
iterate over all curves in the Stein-Watkins database up to
conductor 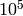 . We could also type for C in d:
...
. We could also type for C in d:
...
To access the data file starting at 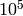 do the
following:
do the
following:
sage: d = SteinWatkinsAllData(1) # optional - stein_watkins_database
sage: C = d.next() # optional - stein_watkins_database
sage: C # optional - stein_watkins_database
Stein-Watkins isogeny class of conductor 100002
sage: C.curves # optional - stein_watkins_database
[[[1, 1, 0, 112, 0], '(8,1,2,1)', 'X', '2'],
[[1, 1, 0, -448, -560], '[4,2,1,2]', 'X', '2']]
Next we access the prime-conductor data:
sage: d = SteinWatkinsPrimeData(0) # optional - stein_watkins_database
sage: C = d.next() # optional - stein_watkins_database
sage: C # optional - stein_watkins_database
Stein-Watkins isogeny class of conductor 11
Each call d.next() gives another elliptic curve of prime conductor:
sage: C = d.next() # optional - stein_watkins_database
sage: C # optional - stein_watkins_database
Stein-Watkins isogeny class of conductor 17
sage: C.curves # optional - stein_watkins_database
[[[1, -1, 1, -1, 0], '[1]', '1', '4'],
[[1, -1, 1, -6, -4], '[2]', '1', '2x'],
[[1, -1, 1, -1, -14], '(4)', '1', '4'],
[[1, -1, 1, -91, -310], '[1]', '1', '2']]
sage: C = d.next() # optional - stein_watkins_database
sage: C # optional - stein_watkins_database
Stein-Watkins isogeny class of conductor 19
Class for iterating through one of the Stein-Watkins database files for all conductors.