Sage includes John Cremona’s tables of elliptic curves in an easy-to-use format. The unique instance of the class CremonaDatabase() gives access to the database.
If the full CremonaDatabase isn’t installed, a mini-version is included by default with Sage. It contains Weierstrass equations, rank, and torsion for curves up to conductor 10000.
The large database includes all curves of conductor up to 120,000 (!). It also includes data related to the BSD conjecture and modular degrees for all of these curves, and generators for the Mordell-Weil groups. To install it type the following in Sage: !sage -i database_cremona_ellcurve-2005.11.03
The name of the database may change as it is updated. Type “!sage -optional” to see the latest package names.
Bases: sage.databases.db.Database
The Cremona database of elliptic curves.
EXAMPLES:
sage: c = CremonaDatabase()
sage: c.allcurves(11)
{'a1': [[0, -1, 1, -10, -20], 0, 5], 'a3': [[0, -1, 1, 0, 0], 0, 5], 'a2': [[0, -1, 1, -7820, -263580], 0, 1]}
Return the allbsd table for conductor N. The entries are:
[id, tamagawa_product, Omega_E, L, Reg_E, Sha_an(E)],
where id is the isogeny class (letter) followed by a number, e.g.,
b3, and L is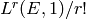 
, where E has rank r.
INPUT:
OUTPUT: dict
Returns the allcurves table of curves of conductor N.
INPUT:
OUTPUT:
Return the allgens table for conductor N.
INPUT:
OUTPUT:
Return the range of conductors that are covered by the database.
OUTPUT:
EXAMPLES:
sage: CremonaDatabase().conductor_range() # random -- depends on database installed
(1, 10000)
Returns the curves table of all optimal curves of conductor N.
INPUT:
OUTPUT:
EXAMPLES:
Optimal curves of conductor 37:
sage: CremonaDatabase().curves(37)
{'a1': [[0, 0, 1, -1, 0], 1, 1], 'b1': [[0, 1, 1, -23, -50], 0, 3]}
Note the ‘h3’, which is the unique case in the tables where the optimal curve doesn’t have label ending in 1:
sage: list(sorted(CremonaDatabase().curves(990).keys()))
['a1', 'b1', 'c1', 'd1', 'e1', 'f1', 'g1', 'h3', 'i1', 'j1', 'k1', 'l1']
Return the degphi table for conductor N.
INPUT:
OUTPUT:
Return an elliptic curve with given label with some data about it from the database pre-filled in.
INPUT:
OUTPUT: EllipticCurve
Returns the elliptic curve in the database of conductor N with minimal ainvs, if it exists, or raises a RuntimeError exception otherwise.
INPUT:
OUTPUT: EllipticCurve
Returns the isogeny class of elliptic curves that are isogenous to the curve with given Cremona label.
INPUT:
OUTPUT:
Returns an iterator through all curves with conductor between Nmin and Nmax-1, inclusive, in the database.
INPUT:
OUTPUT: generator that iterates over EllipticCurve objects.
Returns an iterator through all optimal curves with conductor between Nmin and Nmax-1 in the database.
INPUT:
OUTPUT:
generator that iterates over EllipticCurve objects.
EXAMPLES:
We list optimal curves with conductor up to 20:
sage: [e.cremona_label() for e in CremonaDatabase().iter_optimal([11..20])]
['11a1', '14a1', '15a1', '17a1', '19a1', '20a1']
Note the unfortunate 990h3 special case:
sage: [e.cremona_label() for e in CremonaDatabase().iter_optimal([990])]
['990a1', '990b1', '990c1', '990d1', '990e1', '990f1', '990g1', '990h3', '990i1', '990j1', '990k1', '990l1']
The largest conductor for which the database is complete.
OUTPUT:
EXAMPLES:
sage: CremonaDatabase().largest_conductor() # random -- depends on size of installed database
9999
Returns a list of all curves with conductor between Nmin and Nmax-1, inclusive, in the database.
INPUT:
OUTPUT:
Returns a list of all optimal curves with conductor between Nmin and Nmax-1, inclusive, in the database.
INPUT:
list of EllipticCurve objects.
OUTPUT:
list of EllipticCurve objects.
EXAMPLES:
sage: CremonaDatabase().list_optimal([37])
[Elliptic Curve defined by y^2 + y = x^3 - x over Rational Field,
Elliptic Curve defined by y^2 + y = x^3 + x^2 - 23*x - 50 over Rational Field]
Returns the number of curves stored in the database with conductor N. If N = 0, returns the total number of curves in the database.
If i is nonzero, returns the number of curves in the i-th isogeny class. If i is a Cremona letter code, e.g., ‘a’ or ‘bc’, it is converted to the corresponding number.
INPUT:
OUTPUT: int
EXAMPLES:
sage: c = CremonaDatabase()
sage: c.number_of_curves(11)
3
sage: c.number_of_curves(37)
4
sage: c.number_of_curves(990)
42
sage: num = c.number_of_curves()
Returns the number of isogeny classes of curves in the database of conductor N. If N is 0, return the total number of isogeny classes of curves in the database.
INPUT:
OUTPUT: int
EXAMPLES:
sage: c = CremonaDatabase()
sage: c.number_of_isogeny_classes(11)
1
sage: c.number_of_isogeny_classes(37)
2
sage: num = c.number_of_isogeny_classes()
Returns a random curve from the database.
EXAMPLES:
sage: CremonaDatabase().random() # random -- depends on database installed
Elliptic Curve defined by y^2 + x*y = x^3 - x^2 - 224*x + 3072 over Rational Field
The smallest conductor for which the database is complete. (Always 1.)
OUTPUT:
EXAMPLES:
sage: CremonaDatabase().smallest_conductor()
1
Bases: sage.databases.cremona.LargeCremonaDatabase
A mini version of the Cremona database that contains only the Weierstrass equations, rank and torsion of elliptic curves of conductor up to 10000 and nothing else.
Converts class id string into an integer. Note that this is the inverse of cremona_letter_code.
EXAMPLES:
sage: import sage.databases.cremona as cremona
sage: cremona.class_to_int('ba')
26
sage: cremona.class_to_int('cremona')
821863562
sage: cremona_letter_code(821863562)
'cremona'
Comparison function for curve id strings.
Note
Not the same as standard lexicographic order!
EXAMPLES:
sage: import sage.databases.cremona as cremona
sage: cremona.cmp_code('ba1','z1')
1
By contrast:
sage: cmp('ba1','z1')
-1
Returns the Cremona letter code corresponding to an integer. For example, 0 - a 25 - z 26 - ba 51 - bz 52 - ca 53 - cb etc.
Note
This is just the base 26 representation of n, where a=0, b=1, ..., z=25. This extends the old Cremona notation (counting from 0) for the first 26 classes, and is different for classes above 26.
INPUT:
OUTPUT: str
EXAMPLES:
sage: cremona_letter_code(0)
'a'
sage: cremona_letter_code(26)
'ba'
sage: cremona_letter_code(27)
'bb'
sage: cremona_letter_code(521)
'ub'
sage: cremona_letter_code(53)
'cb'
sage: cremona_letter_code(2005)
'czd'
Returns true if the Cremona id refers to an optimal curve, and false otherwise. The curve is optimal if the id, which is of the form [letter code][number] has number 1.
Note
990h3 is the optimal curve in that class, so doesn’t obey this rule.
INPUT:
OUTPUT: bool
EXAMPLES:
False
sage: is_optimal_id('b1')
True
sage: is_optimal_id('bb1')
True
sage: is_optimal_id('c1')
True
sage: is_optimal_id('c2')
False
Returns the old Cremona letter code corresponding to an integer. integer.
For example,
INPUT:
OUTPUT: str
EXAMPLES:
sage: old_cremona_letter_code(1)
'A'
sage: old_cremona_letter_code(26)
'Z'
sage: old_cremona_letter_code(27)
'AA'
sage: old_cremona_letter_code(521)
'AAAAAAAAAAAAAAAAAAAAA'
sage: old_cremona_letter_code(53)
'AAA'
sage: old_cremona_letter_code(2005)
'CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC'
Given a Cremona label that defines an elliptic curve, e.g., 11A1 or 37B3, parse the label and return the conductor, isogeny class label, and number.
The isogeny number may be omitted, in which case it defaults to 1. If the isogeny number and letter are both omitted, so label is just a string representing a conductor, then the label defaults to ‘A’ and the number to 1.
INPUT:
OUTPUT:
EXAMPLES:
sage: parse_cremona_label('37a2')
(37, 'a', 2)
sage: parse_cremona_label('37b1')
(37, 'b', 1)
sage: parse_cremona_label('10bb2')
(10, 'bb', 2)
Splits class+curve id string into its two parts.
EXAMPLES:
sage: import sage.databases.cremona as cremona
sage: cremona.split_code('ba2')
('ba', '2')