Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Cryptography »

A convenient user interface to various classical ciphers. These include:
These classical cryptosystems support alphabets such as:
AUTHORS:
Bases: sage.crypto.cryptosystem.SymmetricKeyCryptosystem
Create an affine cryptosystem.
Let 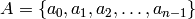 be a non-empty alphabet
consisting of
be a non-empty alphabet
consisting of  unique elements. Define a mapping
unique elements. Define a mapping
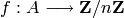 from the alphabet
from the alphabet  to
the set
to
the set 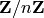 of integers modulo
of integers modulo  , given by
, given by
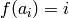 . Thus we can identify each element of the alphabet
. Thus we can identify each element of the alphabet  with a unique integer
with a unique integer 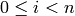 . A key of the affine cipher is an
ordered pair of integers
. A key of the affine cipher is an
ordered pair of integers 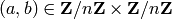 such
that
such
that 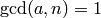 . Therefore the key space is
. Therefore the key space is
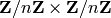 . Since we assume that
. Since we assume that  does not have
repeated elements, the mapping
does not have
repeated elements, the mapping 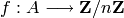 is
bijective. Encryption and decryption functions are both affine functions.
Let
is
bijective. Encryption and decryption functions are both affine functions.
Let 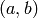 be a secret key, i.e. an element of the key space, and let
be a secret key, i.e. an element of the key space, and let
 be a plaintext character and consequently
be a plaintext character and consequently 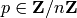 . Then
the ciphertext character
. Then
the ciphertext character  corresponding to
corresponding to  is given by
is given by
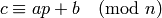
Similarly, given a ciphertext character 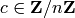 and a secret
key
and a secret
key 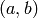 , we can recover the corresponding plaintext character as
follows:
, we can recover the corresponding plaintext character as
follows:
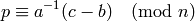
where 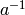 is the inverse of
is the inverse of  modulo
modulo  . Use the bijection
. Use the bijection
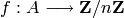 to convert
to convert  and
and  back to
elements of the alphabet
back to
elements of the alphabet  . Currently, only the following alphabet is
supported for the affine cipher:
. Currently, only the following alphabet is
supported for the affine cipher:
EXAMPLES:
Encryption and decryption over the capital letters of the English alphabet:
sage: A = AffineCryptosystem(AlphabeticStrings()); A
Affine cryptosystem on Free alphabetic string monoid on A-Z
sage: P = A.encoding("The affine cryptosystem generalizes the shift cipher.")
sage: P
THEAFFINECRYPTOSYSTEMGENERALIZESTHESHIFTCIPHER
sage: a, b = (9, 13)
sage: C = A.enciphering(a, b, P); C
CYXNGGHAXFKVSCJTVTCXRPXAXKNIHEXTCYXTYHGCFHSYXK
sage: A.deciphering(a, b, C)
THEAFFINECRYPTOSYSTEMGENERALIZESTHESHIFTCIPHER
sage: A.deciphering(a, b, C) == P
True
We can also use functional notation to work through the previous example:
sage: A = AffineCryptosystem(AlphabeticStrings()); A
Affine cryptosystem on Free alphabetic string monoid on A-Z
sage: P = A.encoding("The affine cryptosystem generalizes the shift cipher.")
sage: P
THEAFFINECRYPTOSYSTEMGENERALIZESTHESHIFTCIPHER
sage: a, b = (9, 13)
sage: E = A(a, b); E
Affine cipher on Free alphabetic string monoid on A-Z
sage: C = E(P); C
CYXNGGHAXFKVSCJTVTCXRPXAXKNIHEXTCYXTYHGCFHSYXK
sage: aInv, bInv = A.inverse_key(a, b)
sage: D = A(aInv, bInv); D
Affine cipher on Free alphabetic string monoid on A-Z
sage: D(C)
THEAFFINECRYPTOSYSTEMGENERALIZESTHESHIFTCIPHER
sage: D(C) == P
True
sage: D(C) == P == D(E(P))
True
Encrypting the ciphertext with the inverse key also produces the plaintext:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: P = A.encoding("Encrypt with inverse key.")
sage: a, b = (11, 8)
sage: C = A.enciphering(a, b, P)
sage: P; C
ENCRYPTWITHINVERSEKEY
AVENMRJQSJHSVFANYAOAM
sage: aInv, bInv = A.inverse_key(a, b)
sage: A.enciphering(aInv, bInv, C)
ENCRYPTWITHINVERSEKEY
sage: A.enciphering(aInv, bInv, C) == P
True
For a secret key 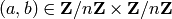 , if
, if 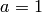 then
any affine cryptosystem with key
then
any affine cryptosystem with key 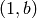 for any
for any 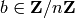 is
a shift cryptosystem. Here is how we can create a Caesar cipher using
an affine cipher:
is
a shift cryptosystem. Here is how we can create a Caesar cipher using
an affine cipher:
sage: caesar = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (1, 3)
sage: P = caesar.encoding("abcdef"); P
ABCDEF
sage: C = caesar.enciphering(a, b, P); C
DEFGHI
sage: caesar.deciphering(a, b, C) == P
True
Any affine cipher with keys of the form
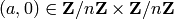 is called a decimation cipher on
the Roman alphabet, or decimation cipher for short:
is called a decimation cipher on
the Roman alphabet, or decimation cipher for short:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: P = A.encoding("A decimation cipher is a specialized affine cipher.")
sage: a, b = (17, 0)
sage: C = A.enciphering(a, b, P)
sage: P; C
ADECIMATIONCIPHERISASPECIALIZEDAFFINECIPHER
AZQIGWALGENIGVPQDGUAUVQIGAFGJQZAHHGNQIGVPQD
sage: A.deciphering(a, b, C) == P
True
Generate a random key for encryption and decryption:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: P = A.encoding("An affine cipher with a random key.")
sage: a, b = A.random_key()
sage: C = A.enciphering(a, b, P)
sage: A.deciphering(a, b, C) == P
True
TESTS:
The binary number system is currently not a supported alphabet of this affine cryptosystem:
sage: AffineCryptosystem(BinaryStrings())
...
TypeError: A (= Free binary string monoid) is not supported as a cipher domain of this affine cryptosystem.
Nor are the octal, hexadecimal, and radix-64 number systems supported:
sage: AffineCryptosystem(OctalStrings())
...
TypeError: A (= Free octal string monoid) is not supported as a cipher domain of this affine cryptosystem.
sage: AffineCryptosystem(HexadecimalStrings())
...
TypeError: A (= Free hexadecimal string monoid) is not supported as a cipher domain of this affine cryptosystem.
sage: AffineCryptosystem(Radix64Strings())
...
TypeError: A (= Free radix 64 string monoid) is not supported as a cipher domain of this affine cryptosystem.
A secret key 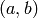 must be an element of
must be an element of 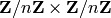 with
with
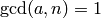 . This rules out the case
. This rules out the case 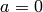 irrespective of the
value of
irrespective of the
value of  . For the upper-case letters of the English alphabet, where
the alphabet size is
. For the upper-case letters of the English alphabet, where
the alphabet size is 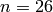 ,
,  cannot take on any even value:
cannot take on any even value:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: A(0, 1)
...
ValueError: (a, b) = (0, 1) is outside the range of acceptable values for a key of this affine cryptosystem.
sage: A(2, 1)
...
ValueError: (a, b) = (2, 1) is outside the range of acceptable values for a key of this affine cryptosystem.
REFERENCES:
| [Sti06] | Douglas R. Stinson. Cryptography: Theory and Practice. 3rd edition, Chapman & Hall/CRC, 2006. |
Attempt a brute force cryptanalysis of the ciphertext C.
INPUT:
OUTPUT:
EXAMPLES:
Cryptanalyze using all possible keys with the option ranking="none":
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (3, 7)
sage: P = A.encoding("Linear"); P
LINEAR
sage: C = A.enciphering(a, b, P)
sage: L = A.brute_force(C)
sage: sorted(L.items())[:26] # display 26 candidate decipherments
<BLANKLINE>
[((1, 0), OFUTHG),
((1, 1), NETSGF),
((1, 2), MDSRFE),
((1, 3), LCRQED),
((1, 4), KBQPDC),
((1, 5), JAPOCB),
((1, 6), IZONBA),
((1, 7), HYNMAZ),
((1, 8), GXMLZY),
((1, 9), FWLKYX),
((1, 10), EVKJXW),
((1, 11), DUJIWV),
((1, 12), CTIHVU),
((1, 13), BSHGUT),
((1, 14), ARGFTS),
((1, 15), ZQFESR),
((1, 16), YPEDRQ),
((1, 17), XODCQP),
((1, 18), WNCBPO),
((1, 19), VMBAON),
((1, 20), ULAZNM),
((1, 21), TKZYML),
((1, 22), SJYXLK),
((1, 23), RIXWKJ),
((1, 24), QHWVJI),
((1, 25), PGVUIH)]
Use the chi-square ranking function, i.e. ranking="chisquare":
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (3, 7)
sage: P = A.encoding("Linear functions for encrypting and decrypting."); P
LINEARFUNCTIONSFORENCRYPTINGANDDECRYPTING
sage: C = A.enciphering(a, b, P)
sage: Rank = A.brute_force(C, ranking="chisquare")
sage: Rank[:10] # display only the top 10 candidate keys
<BLANKLINE>
[((3, 7), LINEARFUNCTIONSFORENCRYPTINGANDDECRYPTING),
((23, 25), VYTCGPBMTENYSTOBSPCTEPIRNYTAGTDDCEPIRNYTA),
((1, 12), CTIHVUKDIBATLIXKLUHIBUPOATINVIEEHBUPOATIN),
((11, 15), HSRYELDAROVSWRQDWLYROLUBVSRIERTTYOLUBVSRI),
((25, 1), NWHIUVFMHOPWEHSFEVIHOVABPWHCUHLLIOVABPWHC),
((25, 7), TCNOABLSNUVCKNYLKBONUBGHVCNIANRROUBGHVCNI),
((15, 4), SHIBVOWZILEHDIJWDOBILOFYEHIRVIGGBLOFYEHIR),
((15, 23), PEFYSLTWFIBEAFGTALYFILCVBEFOSFDDYILCVBEFO),
((7, 10), IDUFHSYXUTEDNULYNSFUTSVGEDURHUMMFTSVGEDUR),
((19, 22), QVETRGABEFUVLENALGTEFGDSUVEHREMMTFGDSUVEH)]
Use the squared differences ranking function, i.e. ranking="squared_differences":
sage: Rank = A.brute_force(C, ranking="squared_differences")
sage: Rank[:10] # display only the top 10 candidate keys
<BLANKLINE>
[((3, 7), LINEARFUNCTIONSFORENCRYPTINGANDDECRYPTING),
((23, 6), GJENRAMXEPYJDEZMDANEPATCYJELREOONPATCYJEL),
((23, 25), VYTCGPBMTENYSTOBSPCTEPIRNYTAGTDDCEPIRNYTA),
((19, 22), QVETRGABEFUVLENALGTEFGDSUVEHREMMTFGDSUVEH),
((19, 9), DIRGETNORSHIYRANYTGRSTQFHIRUERZZGSTQFHIRU),
((23, 18), KNIRVEQBITCNHIDQHERITEXGCNIPVISSRTEXGCNIP),
((17, 16), GHORBEIDOJMHFOVIFEROJETWMHOZBOAARJETWMHOZ),
((21, 14), AHEZRMOFEVQHTEBOTMZEVMNIQHEDREKKZVMNIQHED),
((1, 12), CTIHVUKDIBATLIXKLUHIBUPOATINVIEEHBUPOATIN),
((7, 18), SNEPRCIHEDONXEVIXCPEDCFQONEBREWWPDCFQONEB)]
TESTS:
Currently, the binary number system is not supported as an alphabet of this affine cryptosystem:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: BinStr = BinaryStrings()
sage: C = BinStr.encoding("abc")
sage: A.brute_force(C)
...
TypeError: Ciphertext must be encoded using one of the supported cipher domains of this affine cryptosystem.
Nor are the octal, hexadecimal, and radix-64 number systems supported:
sage: OctStr = OctalStrings()
sage: C = OctStr([1, 2, 3])
sage: A.brute_force(C)
...
TypeError: Ciphertext must be encoded using one of the supported cipher domains of this affine cryptosystem.
sage: HexStr = HexadecimalStrings()
sage: C = HexStr.encoding("abc")
sage: A.brute_force(C)
...
TypeError: Ciphertext must be encoded using one of the supported cipher domains of this affine cryptosystem.
sage: RadStr = Radix64Strings()
sage: C = RadStr([1, 2, 3])
sage: A.brute_force(C)
...
TypeError: Ciphertext must be encoded using one of the supported cipher domains of this affine cryptosystem.
Only the chi-square and squared-differences ranking functions are currently supported. The keyword ranking must take on either of the values "none", "chisquare" or "squared_differences":
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (3, 7)
sage: P = A.encoding("Linear")
sage: C = A.enciphering(a, b, P)
sage: A.brute_force(C, ranking="chi")
...
ValueError: Keyword 'ranking' must be either 'none', 'chisquare', or 'squared_differences'.
sage: A.brute_force(C, ranking="")
...
ValueError: Keyword 'ranking' must be either 'none', 'chisquare', or 'squared_differences'.
Decrypt the ciphertext C with the key (a, b) using affine cipher decryption.
INPUT:
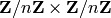 such that
such that 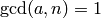 with
with  being the size of the ciphertext and plaintext spaces.
being the size of the ciphertext and plaintext spaces.OUTPUT:
EXAMPLES:
Decryption over the capital letters of the English alphabet:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (5, 2)
sage: P = A.encoding("Affine functions are linear functions.")
sage: C = A.enciphering(a, b, P); C
CBBQPWBYPMTQUPOCJWFQPWCJBYPMTQUPO
sage: P == A.deciphering(a, b, C)
True
The previous example can also be worked through using functional notation:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (5, 2)
sage: P = A.encoding("Affine functions are linear functions.")
sage: E = A(a, b); E
Affine cipher on Free alphabetic string monoid on A-Z
sage: C = E(P); C
CBBQPWBYPMTQUPOCJWFQPWCJBYPMTQUPO
sage: aInv, bInv = A.inverse_key(a, b)
sage: D = A(aInv, bInv); D
Affine cipher on Free alphabetic string monoid on A-Z
sage: D(C) == P
True
If the ciphertext is an empty string, then the plaintext is also an empty string regardless of the value of the secret key:
sage: a, b = A.random_key()
sage: A.deciphering(a, b, A.encoding(""))
<BLANKLINE>
sage: A.deciphering(a, b, A.encoding(" "))
<BLANKLINE>
TESTS:
The key must be an ordered pair
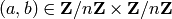 with
with  being the size of the
plaintext and ciphertext spaces. Furthermore,
being the size of the
plaintext and ciphertext spaces. Furthermore,  must be
relatively prime to
must be
relatively prime to  , i.e.
, i.e. 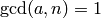 :
:
sage: A.deciphering(2, 6, P)
...
ValueError: (a, b) = (2, 6) is outside the range of acceptable values for a key of this affine cipher.
Encrypt the plaintext P with the key (a, b) using affine cipher encryption.
INPUT:
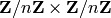 such that
such that 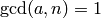 with
with  being the size of the ciphertext and plaintext spaces.
being the size of the ciphertext and plaintext spaces.OUTPUT:
EXAMPLES:
Encryption over the capital letters of the English alphabet:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (3, 6)
sage: P = A.encoding("Affine ciphers work with linear functions.")
sage: A.enciphering(a, b, P)
GVVETSMEZBSFIUWFKUELBNETSGFVOTMLEWTI
Now work through the previous example using functional notation:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (3, 6)
sage: P = A.encoding("Affine ciphers work with linear functions.")
sage: E = A(a, b); E
Affine cipher on Free alphabetic string monoid on A-Z
sage: E(P)
GVVETSMEZBSFIUWFKUELBNETSGFVOTMLEWTI
If the plaintext is an empty string, then the ciphertext is also an empty string regardless of the value of the secret key:
sage: a, b = A.random_key()
sage: A.enciphering(a, b, A.encoding(""))
<BLANKLINE>
sage: A.enciphering(a, b, A.encoding(" "))
<BLANKLINE>
TESTS:
The key must be an ordered pair
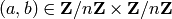 with
with  being the size of the
plaintext and ciphertext spaces. Furthermore,
being the size of the
plaintext and ciphertext spaces. Furthermore,  must be
relatively prime to
must be
relatively prime to  , i.e.
, i.e. 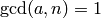 :
:
sage: A.enciphering(2, 6, P)
...
ValueError: (a, b) = (2, 6) is outside the range of acceptable values for a key of this affine cryptosystem.
The encoding of the string S over the string monoid of this affine cipher. For example, if the string monoid of this cryptosystem is AlphabeticStringMonoid, then the encoding of S would be its upper-case equivalent stripped of all non-alphabetic characters. Only the following alphabet is supported for the affine cipher:
INPUT:
OUTPUT:
EXAMPLES:
Encoding over the upper-case letters of the English alphabet:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: A.encoding("Affine cipher over capital letters of the English alphabet.")
AFFINECIPHEROVERCAPITALLETTERSOFTHEENGLISHALPHABET
The argument S can be an empty string, in which case an empty string is returned:
sage: AffineCryptosystem(AlphabeticStrings()).encoding("")
<BLANKLINE>
The inverse key corresponding to the secret key 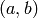 . If
. If  is
a plaintext character so that
is
a plaintext character so that 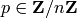 and
and  is the
alphabet size, then the ciphertext
is the
alphabet size, then the ciphertext  corresponding to
corresponding to  is
is
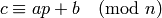
As 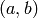 is a key, then the multiplicative inverse
is a key, then the multiplicative inverse 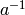 exists and the original plaintext can be recovered as follows
exists and the original plaintext can be recovered as follows
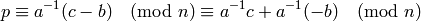
Therefore the ordered pair 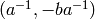 is the inverse key
corresponding to
is the inverse key
corresponding to 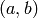 .
.
INPUT:
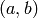 must be an element of
must be an element of 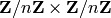 such that
such that
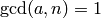 .
.OUTPUT:
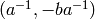 corresponding to
corresponding to 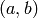 .
.EXAMPLES:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (1, 2)
sage: A.inverse_key(a, b)
(1, 24)
sage: A.inverse_key(3, 2)
(9, 8)
Suppose that the plaintext and ciphertext spaces are the capital
letters of the English alphabet so that 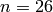 . If
. If 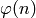 is the Euler phi function of
is the Euler phi function of  , then there are
, then there are 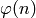 integers
integers 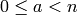 that are relatively prime to
that are relatively prime to  . For the
capital letters of the English alphabet, there are 12 such integers
relatively prime to
. For the
capital letters of the English alphabet, there are 12 such integers
relatively prime to  :
:
sage: euler_phi(A.alphabet_size())
12
And here is a list of those integers:
sage: n = A.alphabet_size()
sage: L = [i for i in xrange(n) if gcd(i, n) == 1]; L
[1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25]
Then a secret key 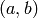 of this shift cryptosystem is
such that
of this shift cryptosystem is
such that  is an element of the list L in the last example.
Any inverse key
is an element of the list L in the last example.
Any inverse key 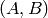 corresponding to
corresponding to 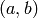 is such that
is such that
 is also in the list L above:
is also in the list L above:
sage: a, b = (3, 9)
sage: a in L
True
sage: aInv, bInv = A.inverse_key(a, b)
sage: aInv, bInv
(9, 23)
sage: aInv in L
True
TESTS:
Any ordered pair of the form 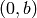 for any integer
for any integer  cannot be
a secret key of this affine cipher. Hence
cannot be
a secret key of this affine cipher. Hence 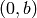 does not have
a corresponding inverse key:
does not have
a corresponding inverse key:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: A.inverse_key(0, 1)
...
ValueError: (a, b) = (0, 1) is outside the range of acceptable values for a key of this affine cipher.
Generate a random key within the key space of this affine cipher.
The generated secret key is an ordered pair
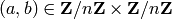 with
with  being the size of
the cipher domain and
being the size of
the cipher domain and 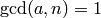 . Let
. Let 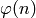 denote
the Euler phi function of
denote
the Euler phi function of  . Then the affine cipher has
. Then the affine cipher has
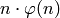 possible keys (see page 10 of [Sti06]).
possible keys (see page 10 of [Sti06]).
OUTPUT:
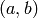 .
.EXAMPLES:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: A.random_key() # random
(17, 25)
If 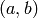 is a secret key and
is a secret key and  is the size of the plaintext and
ciphertext alphabets, then
is the size of the plaintext and
ciphertext alphabets, then 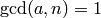 :
:
sage: a, b = A.random_key()
sage: n = A.alphabet_size()
sage: gcd(a, n)
1
Use the chi-square statistic to rank all possible keys. Currently, this method only applies to the capital letters of the English alphabet.
ALGORITHM:
Consider a non-empty alphabet  consisting of
consisting of  elements, and let
elements, and let  be a ciphertext encoded using elements of
be a ciphertext encoded using elements of
 . The plaintext
. The plaintext  corresponding to
corresponding to  is also encoded using
elements of
is also encoded using
elements of  . Let
. Let  be a candidate decipherment of
be a candidate decipherment of  ,
i.e.
,
i.e.  is the result of attempting to decrypt
is the result of attempting to decrypt  using a key
using a key
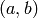 which is not necessarily the same key used to encrypt
which is not necessarily the same key used to encrypt  .
Suppose
.
Suppose 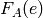 is the characteristic frequency probability of
is the characteristic frequency probability of
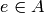 and let
and let 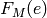 be the message frequency probability with
respect to
be the message frequency probability with
respect to  . The characteristic frequency probability
distribution of an alphabet is the expected frequency probability
distribution for that alphabet. The message frequency probability
distribution of
. The characteristic frequency probability
distribution of an alphabet is the expected frequency probability
distribution for that alphabet. The message frequency probability
distribution of  provides a distribution of the ratio of character
occurrences over message length. One can interpret the
characteristic frequency probability
provides a distribution of the ratio of character
occurrences over message length. One can interpret the
characteristic frequency probability 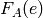 as the expected
probability, while the message frequency probability
as the expected
probability, while the message frequency probability 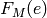 is
the observed probability. If
is
the observed probability. If  is of length
is of length  , then the observed
frequency of
, then the observed
frequency of 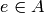 is
is
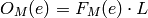
and the expected frequency of 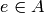 is
is
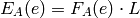
The chi-square rank 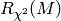 of
of  corresponding to a key
corresponding to a key
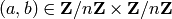 is given by
is given by
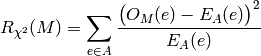
Cryptanalysis by exhaustive key search produces a candidate
decipherment 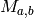 for each possible key
for each possible key 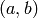 . For a set
. For a set
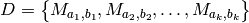 of all candidate decipherments corresponding to a ciphertext
of all candidate decipherments corresponding to a ciphertext  ,
the smaller is the rank
,
the smaller is the rank 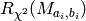 the more likely
that
the more likely
that 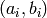 is the secret key. This key ranking method is
based on the Pearson chi-square test [PearsonTest09].
is the secret key. This key ranking method is
based on the Pearson chi-square test [PearsonTest09].
INPUT:
OUTPUT:
EXAMPLES:
Use the chi-square statistic to rank all possible keys and their corresponding decipherment:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (3, 7)
sage: P = A.encoding("Line.")
sage: C = A.enciphering(a, b, P)
sage: Plist = A.brute_force(C)
sage: Rank = A.rank_by_chi_square(C, Plist)
sage: Rank[:10] # display only the top 10 candidate keys
<BLANKLINE>
[((1, 1), NETS),
((3, 7), LINE),
((17, 20), STAD),
((5, 2), SLOT),
((5, 5), HADI),
((9, 25), TSLI),
((17, 15), DELO),
((15, 6), ETUN),
((21, 8), ELID),
((7, 17), HCTE)]
As more ciphertext is available, the reliability of the chi-square ranking function increases:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (11, 24)
sage: P = A.encoding("Longer message is more information for cryptanalysis.")
sage: C = A.enciphering(a, b, P)
sage: Plist = A.brute_force(C)
sage: Rank = A.rank_by_chi_square(C, Plist)
sage: Rank[:10] # display only the top 10 candidate keys
<BLANKLINE>
[((11, 24), LONGERMESSAGEISMOREINFORMATIONFORCRYPTANALYSIS),
((17, 9), INURFSBFLLHRFDLBNSFDUYNSBHEDNUYNSTSVGEHUHIVLDL),
((9, 18), RMFIUHYUOOSIUWOYMHUWFBMHYSVWMFBMHGHETVSFSREOWO),
((15, 12), VSTACPUCOOGACYOUSPCYTBSPUGNYSTBSPEPIRNGTGVIOYO),
((3, 22), PAFOYLKYGGSOYEGKALYEFTALKSBEAFTALILCVBSFSPCGEG),
((25, 3), OHSRNADNPPFRNVPDHANVSCHADFEVHSCHAJABWEFSFOBPVP),
((7, 25), GHYNVIPVRRLNVFRPHIVFYEHIPLAFHYEHIDITQALYLGTRFR),
((5, 2), NEHCIVKISSUCIWSKEVIWHFEVKUPWEHFEVOVABPUHUNASWS),
((15, 25), IFGNPCHPBBTNPLBHFCPLGOFCHTALFGOFCRCVEATGTIVBLB),
((9, 6), BWPSERIEYYCSEGYIWREGPLWRICFGWPLWRQRODFCPCBOYGY)]
TESTS:
The ciphertext cannot be an empty string:
sage: A.rank_by_chi_square("", Plist)
...
AttributeError: 'str' object has no attribute 'parent'
sage: A.rank_by_chi_square(A.encoding(""), Plist)
...
ValueError: The ciphertext must be a non-empty string.
sage: A.rank_by_chi_square(A.encoding(" "), Plist)
...
ValueError: The ciphertext must be a non-empty string.
The ciphertext must be encoded using the capital letters of the English alphabet as implemented in AlphabeticStrings():
sage: H = HexadecimalStrings()
sage: A.rank_by_chi_square(H.encoding("shift"), Plist)
...
TypeError: The ciphertext must be capital letters of the English alphabet.
sage: B = BinaryStrings()
sage: A.rank_by_chi_square(B.encoding("shift"), Plist)
...
TypeError: The ciphertext must be capital letters of the English alphabet.
The dictionary pdict cannot be empty:
sage: A.rank_by_chi_square(C, {})
...
KeyError: (1, 0)
Use the squared-differences measure to rank all possible keys. Currently, this method only applies to the capital letters of the English alphabet.
ALGORITHM:
Consider a non-empty alphabet  consisting of
consisting of  elements, and let
elements, and let  be a ciphertext encoded using elements of
be a ciphertext encoded using elements of
 . The plaintext
. The plaintext  corresponding to
corresponding to  is also encoded using
elements of
is also encoded using
elements of  . Let
. Let  be a candidate decipherment of
be a candidate decipherment of  ,
i.e.
,
i.e.  is the result of attempting to decrypt
is the result of attempting to decrypt  using a key
using a key
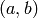 which is not necessarily the same key used to encrypt
which is not necessarily the same key used to encrypt  .
Suppose
.
Suppose 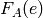 is the characteristic frequency probability of
is the characteristic frequency probability of
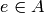 and let
and let 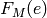 be the message frequency probability with
respect to
be the message frequency probability with
respect to  . The characteristic frequency probability
distribution of an alphabet is the expected frequency probability
distribution for that alphabet. The message frequency probability
distribution of
. The characteristic frequency probability
distribution of an alphabet is the expected frequency probability
distribution for that alphabet. The message frequency probability
distribution of  provides a distribution of the ratio of character
occurrences over message length. One can interpret the
characteristic frequency probability
provides a distribution of the ratio of character
occurrences over message length. One can interpret the
characteristic frequency probability 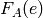 as the expected
probability, while the message frequency probability
as the expected
probability, while the message frequency probability 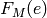 is
the observed probability. If
is
the observed probability. If  is of length
is of length  , then the observed
frequency of
, then the observed
frequency of 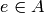 is
is
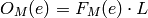
and the expected frequency of 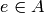 is
is
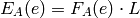
The squared-differences, or residual sum of squares, rank
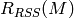 of
of  corresponding to a key
corresponding to a key
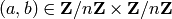 is given by
is given by
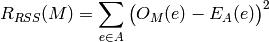
Cryptanalysis by exhaustive key search produces a candidate
decipherment 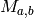 for each possible key
for each possible key 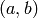 . For a set
. For a set
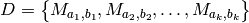 of all candidate decipherments corresponding to a ciphertext
of all candidate decipherments corresponding to a ciphertext  ,
the smaller is the rank
,
the smaller is the rank 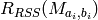 the more likely
that
the more likely
that 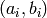 is the secret key. This key ranking method is
based on the residual sum of squares measure [RSS09].
is the secret key. This key ranking method is
based on the residual sum of squares measure [RSS09].
INPUT:
OUTPUT:
EXAMPLES:
Use the method of squared differences to rank all possible keys and their corresponding decipherment:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (3, 7)
sage: P = A.encoding("Line.")
sage: C = A.enciphering(a, b, P)
sage: Plist = A.brute_force(C)
sage: Rank = A.rank_by_squared_differences(C, Plist)
sage: Rank[:10] # display only the top 10 candidate keys
<BLANKLINE>
[((1, 1), NETS),
((15, 6), ETUN),
((7, 17), HCTE),
((3, 7), LINE),
((17, 15), DELO),
((9, 4), EDWT),
((9, 9), POHE),
((21, 8), ELID),
((17, 20), STAD),
((7, 18), SNEP)]
As more ciphertext is available, the reliability of the squared-differences ranking function increases:
sage: A = AffineCryptosystem(AlphabeticStrings())
sage: a, b = (11, 24)
sage: P = A.encoding("Longer message is more information for cryptanalysis.")
sage: C = A.enciphering(a, b, P)
sage: Plist = A.brute_force(C)
sage: Rank = A.rank_by_squared_differences(C, Plist)
sage: Rank[:10] # display only the top 10 candidate keys
<BLANKLINE>
[((11, 24), LONGERMESSAGEISMOREINFORMATIONFORCRYPTANALYSIS),
((9, 14), DYRUGTKGAAEUGIAKYTGIRNYTKEHIYRNYTSTQFHEREDQAIA),
((23, 24), DSNEUHIUMMAEUOMISHUONZSHIAROSNZSHKHQXRANADQMOM),
((23, 1), ETOFVIJVNNBFVPNJTIVPOATIJBSPTOATILIRYSBOBERNPN),
((21, 16), VEBGANYAQQOGAMQYENAMBDENYOTMEBDENUNIHTOBOVIQMQ),
((7, 12), TULAIVCIEEYAISECUVISLRUVCYNSULRUVQVGDNYLYTGESE),
((5, 20), ZQTOUHWUEEGOUIEWQHUITRQHWGBIQTRQHAHMNBGTGZMEIE),
((21, 8), JSPUOBMOEECUOAEMSBOAPRSBMCHASPRSBIBWVHCPCJWEAE),
((25, 7), SLWVREHRTTJVRZTHLERZWGLEHJIZLWGLENEFAIJWJSFTZT),
((25, 15), ATEDZMPZBBRDZHBPTMZHEOTMPRQHTEOTMVMNIQRERANBHB)]
TESTS:
The ciphertext cannot be an empty string:
sage: A.rank_by_squared_differences("", Plist)
...
AttributeError: 'str' object has no attribute 'parent'
sage: A.rank_by_squared_differences(A.encoding(""), Plist)
...
ValueError: The ciphertext must be a non-empty string.
sage: A.rank_by_squared_differences(A.encoding(" "), Plist)
...
ValueError: The ciphertext must be a non-empty string.
The ciphertext must be encoded using the capital letters of the English alphabet as implemented in AlphabeticStrings():
sage: H = HexadecimalStrings()
sage: A.rank_by_squared_differences(H.encoding("line"), Plist)
...
TypeError: The ciphertext must be capital letters of the English alphabet.
sage: B = BinaryStrings()
sage: A.rank_by_squared_differences(B.encoding("line"), Plist)
...
TypeError: The ciphertext must be capital letters of the English alphabet.
The dictionary pdict cannot be empty:
sage: A.rank_by_squared_differences(C, {})
...
KeyError: (1, 0)
Bases: sage.crypto.cryptosystem.SymmetricKeyCryptosystem
Create a Hill cryptosystem defined by the  x
x  matrix space
over
matrix space
over 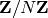 , where
, where  is the alphabet size of
the string monoid S.
is the alphabet size of
the string monoid S.
INPUT:
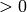 ; the block length of matrices that specify
block permutations
; the block length of matrices that specify
block permutationsOUTPUT:
EXAMPLES:
sage: S = AlphabeticStrings()
sage: E = HillCryptosystem(S,3)
sage: E
Hill cryptosystem on Free alphabetic string monoid on A-Z of block length 3
sage: R = IntegerModRing(26)
sage: M = MatrixSpace(R,3,3)
sage: A = M([[1,0,1],[0,1,1],[2,2,3]])
sage: A
[1 0 1]
[0 1 1]
[2 2 3]
sage: e = E(A)
sage: e
Hill cipher on Free alphabetic string monoid on A-Z of block length 3
sage: e(S("LAMAISONBLANCHE"))
JYVKSKQPELAYKPV
TESTS:
sage: S = AlphabeticStrings()
sage: E = HillCryptosystem(S,3)
sage: E == loads(dumps(E))
True
The row or column dimension of a matrix specifying a block permutation. Encryption and decryption keys of a Hill cipher are square matrices, i.e. the row and column dimensions of an encryption or decryption key are the same. This row/column dimension is referred to as the block length.
OUTPUT:
EXAMPLES:
sage: A = AlphabeticStrings()
sage: n = randint(1, A.ngens() - 1)
sage: H = HillCryptosystem(A, n)
sage: H.block_length() == n
True
Decrypt the ciphertext C using the key A.
INPUT:
OUTPUT:
EXAMPLES:
sage: H = HillCryptosystem(AlphabeticStrings(), 3)
sage: K = H.random_key()
sage: M = H.encoding("Good day, mate! How ya going?")
sage: H.deciphering(K, H.enciphering(K, M)) == M
True
Encrypt the plaintext M using the key A.
INPUT:
OUTPUT:
EXAMPLES:
sage: H = HillCryptosystem(AlphabeticStrings(), 3)
sage: K = H.random_key()
sage: M = H.encoding("Good day, mate! How ya going?")
sage: H.deciphering(K, H.enciphering(K, M)) == M
True
The encoding of the string M over the string monoid of this Hill cipher. For example, if the string monoid of this Hill cipher is AlphabeticStringMonoid, then the encoding of M would be its upper-case equivalent stripped of all non-alphabetic characters.
INPUT:
OUTPUT:
EXAMPLES:
sage: M = "The matrix cipher by Lester S. Hill."
sage: A = AlphabeticStrings()
sage: H = HillCryptosystem(A, 7)
sage: H.encoding(M) == A.encoding(M)
True
The inverse key corresponding to the key A.
INPUT:
OUTPUT:
EXAMPLES:
sage: S = AlphabeticStrings()
sage: E = HillCryptosystem(S,3)
sage: A = E.random_key()
sage: B = E.inverse_key(A)
sage: M = S("LAMAISONBLANCHE")
sage: e = E(A)
sage: c = E(B)
sage: c(e(M))
LAMAISONBLANCHE
A random key within the key space of this Hill cipher. That is,
generate a random  x
x  matrix to be used as a block
permutation, where
matrix to be used as a block
permutation, where  is the block length of this Hill cipher. If
is the block length of this Hill cipher. If
 is the size of the cryptosystem alphabet, then there are
is the size of the cryptosystem alphabet, then there are
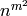 possible keys. However the number of valid keys,
i.e. invertible
possible keys. However the number of valid keys,
i.e. invertible  x
x  square matrices, is smaller than
square matrices, is smaller than
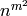 .
.
OUTPUT:
EXAMPLES:
sage: A = AlphabeticStrings()
sage: n = 3
sage: H = HillCryptosystem(A, n)
sage: K = H.random_key()
sage: Ki = H.inverse_key(K)
sage: M = "LAMAISONBLANCHE"
sage: e = H(K)
sage: d = H(Ki)
sage: d(e(A(M))) == A(M)
True
Bases: sage.crypto.cryptosystem.SymmetricKeyCryptosystem
Create a shift cryptosystem.
Let 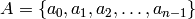 be a non-empty alphabet
consisting of
be a non-empty alphabet
consisting of  unique elements. Define a mapping
unique elements. Define a mapping
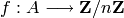 from the alphabet
from the alphabet  to
the set
to
the set 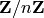 of integers modulo
of integers modulo  , given by
, given by
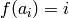 . Thus we can identify each element of the alphabet
. Thus we can identify each element of the alphabet  with a unique integer
with a unique integer 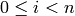 . A key of the shift cipher is an
integer
. A key of the shift cipher is an
integer 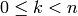 . Therefore the key space is
. Therefore the key space is 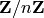 . Since
we assume that
. Since
we assume that  does not have repeated elements, the mapping
does not have repeated elements, the mapping
 is bijective.
Encryption works by moving along the alphabet by
is bijective.
Encryption works by moving along the alphabet by  positions, with
wrap around. Decryption reverses the process by moving backwards by
positions, with
wrap around. Decryption reverses the process by moving backwards by
 positions, with wrap around. More generally, let
positions, with wrap around. More generally, let  be a secret key,
i.e. an element of the key space, and let
be a secret key,
i.e. an element of the key space, and let  be a plaintext
character and consequently
be a plaintext
character and consequently 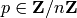 . Then the ciphertext
character
. Then the ciphertext
character  corresponding to
corresponding to  is given by
is given by
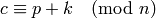
Similarly, given a ciphertext character 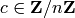 and a secret
key
and a secret
key  , we can recover the corresponding plaintext character as follows:
, we can recover the corresponding plaintext character as follows:
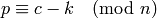
Use the bijection 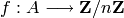 to convert
to convert  and
and  back to elements of the alphabet
back to elements of the alphabet  . Currently, the following
alphabets are supported for the shift cipher:
. Currently, the following
alphabets are supported for the shift cipher:
EXAMPLES:
Some examples illustrating encryption and decryption over various alphabets. Here is an example over the upper-case letters of the English alphabet:
sage: S = ShiftCryptosystem(AlphabeticStrings()); S
Shift cryptosystem on Free alphabetic string monoid on A-Z
sage: P = S.encoding("The shift cryptosystem generalizes the Caesar cipher.")
sage: P
THESHIFTCRYPTOSYSTEMGENERALIZESTHECAESARCIPHER
sage: K = 7
sage: C = S.enciphering(K, P); C
AOLZOPMAJYFWAVZFZALTNLULYHSPGLZAOLJHLZHYJPWOLY
sage: S.deciphering(K, C)
THESHIFTCRYPTOSYSTEMGENERALIZESTHECAESARCIPHER
sage: S.deciphering(K, C) == P
True
The previous example can also be done as follows:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: P = S.encoding("The shift cryptosystem generalizes the Caesar cipher.")
sage: K = 7
sage: E = S(K); E
Shift cipher on Free alphabetic string monoid on A-Z
sage: C = E(P); C
AOLZOPMAJYFWAVZFZALTNLULYHSPGLZAOLJHLZHYJPWOLY
sage: D = S(S.inverse_key(K)); D
Shift cipher on Free alphabetic string monoid on A-Z
sage: D(C) == P
True
sage: D(C) == P == D(E(P))
True
Over the hexadecimal number system:
sage: S = ShiftCryptosystem(HexadecimalStrings()); S
Shift cryptosystem on Free hexadecimal string monoid
sage: P = S.encoding("Encryption & decryption shifts along the alphabet."); P
456e6372797074696f6e20262064656372797074696f6e2073686966747320616c6f6e672074686520616c7068616265742e
sage: K = 5
sage: C = S.enciphering(K, P); C
9ab3b8c7cec5c9beb4b3757b75b9bab8c7cec5c9beb4b375c8bdbebbc9c875b6b1b4b3bc75c9bdba75b6b1c5bdb6b7bac973
sage: S.deciphering(K, C)
456e6372797074696f6e20262064656372797074696f6e2073686966747320616c6f6e672074686520616c7068616265742e
sage: S.deciphering(K, C) == P
True
And over the binary number system:
sage: S = ShiftCryptosystem(BinaryStrings()); S
Shift cryptosystem on Free binary string monoid
sage: P = S.encoding("The binary alphabet is very insecure."); P
01010100011010000110010100100000011000100110100101101110011000010111001001111001001000000110000101101100011100000110100001100001011000100110010101110100001000000110100101110011001000000111011001100101011100100111100100100000011010010110111001110011011001010110001101110101011100100110010100101110
sage: K = 1
sage: C = S.enciphering(K, P); C
10101011100101111001101011011111100111011001011010010001100111101000110110000110110111111001111010010011100011111001011110011110100111011001101010001011110111111001011010001100110111111000100110011010100011011000011011011111100101101001000110001100100110101001110010001010100011011001101011010001
sage: S.deciphering(K, C)
01010100011010000110010100100000011000100110100101101110011000010111001001111001001000000110000101101100011100000110100001100001011000100110010101110100001000000110100101110011001000000111011001100101011100100111100100100000011010010110111001110011011001010110001101110101011100100110010100101110
sage: S.deciphering(K, C) == P
True
A shift cryptosystem with key 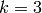 is commonly referred to as the
Caesar cipher. Create a Caesar cipher over the upper-case letters of the
English alphabet:
is commonly referred to as the
Caesar cipher. Create a Caesar cipher over the upper-case letters of the
English alphabet:
sage: caesar = ShiftCryptosystem(AlphabeticStrings())
sage: K = 3
sage: P = caesar.encoding("abcdef"); P
ABCDEF
sage: C = caesar.enciphering(K, P); C
DEFGHI
sage: caesar.deciphering(K, C) == P
True
Generate a random key for encryption and decryption:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: P = S.encoding("Shift cipher with a random key.")
sage: K = S.random_key()
sage: C = S.enciphering(K, P)
sage: S.deciphering(K, C) == P
True
Decrypting with the key K is equivalent to encrypting with its corresponding inverse key:
sage: S.enciphering(S.inverse_key(K), C) == P
True
TESTS:
Currently, the octal number system is not supported as an alphabet for this shift cryptosystem:
sage: ShiftCryptosystem(OctalStrings())
...
TypeError: A (= Free octal string monoid) is not supported as a cipher domain of this shift cryptosystem.
Nor is the radix-64 number system supported:
sage: ShiftCryptosystem(Radix64Strings())
...
TypeError: A (= Free radix 64 string monoid) is not supported as a cipher domain of this shift cryptosystem.
Testing of dumping and loading objects:
sage: SA = ShiftCryptosystem(AlphabeticStrings())
sage: SA == loads(dumps(SA))
True
sage: SH = ShiftCryptosystem(HexadecimalStrings())
sage: SH == loads(dumps(SH))
True
sage: SB = ShiftCryptosystem(BinaryStrings())
sage: SB == loads(dumps(SB))
True
The key K must satisfy the inequality 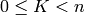 with
with  being the size of the plaintext, ciphertext, and key spaces. For the
shift cryptosystem, all these spaces are the same alphabet. This
inequality must be satisfied for each of the supported alphabets.
The capital letters of the English alphabet:
being the size of the plaintext, ciphertext, and key spaces. For the
shift cryptosystem, all these spaces are the same alphabet. This
inequality must be satisfied for each of the supported alphabets.
The capital letters of the English alphabet:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: S(2 + S.alphabet_size())
...
ValueError: K (=28) is outside the range of acceptable values for a key of this shift cryptosystem.
sage: S(-2)
...
ValueError: K (=-2) is outside the range of acceptable values for a key of this shift cryptosystem.
The hexadecimal number system:
sage: S = ShiftCryptosystem(HexadecimalStrings())
sage: S(1 + S.alphabet_size())
...
ValueError: K (=17) is outside the range of acceptable values for a key of this shift cryptosystem.
sage: S(-1)
...
ValueError: K (=-1) is outside the range of acceptable values for a key of this shift cryptosystem.
The binary number system:
sage: S = ShiftCryptosystem(BinaryStrings())
sage: S(1 + S.alphabet_size())
...
ValueError: K (=3) is outside the range of acceptable values for a key of this shift cryptosystem.
sage: S(-2)
...
ValueError: K (=-2) is outside the range of acceptable values for a key of this shift cryptosystem.
Attempt a brute force cryptanalysis of the ciphertext C.
INPUT:
OUTPUT:
EXAMPLES:
Cryptanalyze using all possible keys for various alphabets. Over the upper-case letters of the English alphabet:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: P = S.encoding("The shift cryptosystem generalizes the Caesar cipher.")
sage: K = 7
sage: C = S.enciphering(K, P)
sage: Dict = S.brute_force(C)
sage: for k in xrange(len(Dict)):
... if Dict[k] == P:
... print "key =", k
...
key = 7
Over the hexadecimal number system:
sage: S = ShiftCryptosystem(HexadecimalStrings())
sage: P = S.encoding("Encryption & decryption shifts along the alphabet.")
sage: K = 5
sage: C = S.enciphering(K, P)
sage: Dict = S.brute_force(C)
sage: for k in xrange(len(Dict)):
... if Dict[k] == P:
... print "key =", k
...
key = 5
And over the binary number system:
sage: S = ShiftCryptosystem(BinaryStrings())
sage: P = S.encoding("The binary alphabet is very insecure.")
sage: K = 1
sage: C = S.enciphering(K, P)
sage: Dict = S.brute_force(C)
sage: for k in xrange(len(Dict)):
... if Dict[k] == P:
... print "key =", k
...
key = 1
Don’t use any ranking functions, i.e. ranking="none":
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: P = S.encoding("Shifting using modular arithmetic.")
sage: K = 8
sage: C = S.enciphering(K, P)
sage: pdict = S.brute_force(C)
sage: sorted(pdict.items())
<BLANKLINE>
[(0, APQNBQVOCAQVOUWLCTIZIZQBPUMBQK),
(1, ZOPMAPUNBZPUNTVKBSHYHYPAOTLAPJ),
(2, YNOLZOTMAYOTMSUJARGXGXOZNSKZOI),
(3, XMNKYNSLZXNSLRTIZQFWFWNYMRJYNH),
(4, WLMJXMRKYWMRKQSHYPEVEVMXLQIXMG),
(5, VKLIWLQJXVLQJPRGXODUDULWKPHWLF),
(6, UJKHVKPIWUKPIOQFWNCTCTKVJOGVKE),
(7, TIJGUJOHVTJOHNPEVMBSBSJUINFUJD),
(8, SHIFTINGUSINGMODULARARITHMETIC),
(9, RGHESHMFTRHMFLNCTKZQZQHSGLDSHB),
(10, QFGDRGLESQGLEKMBSJYPYPGRFKCRGA),
(11, PEFCQFKDRPFKDJLARIXOXOFQEJBQFZ),
(12, ODEBPEJCQOEJCIKZQHWNWNEPDIAPEY),
(13, NCDAODIBPNDIBHJYPGVMVMDOCHZODX),
(14, MBCZNCHAOMCHAGIXOFULULCNBGYNCW),
(15, LABYMBGZNLBGZFHWNETKTKBMAFXMBV),
(16, KZAXLAFYMKAFYEGVMDSJSJALZEWLAU),
(17, JYZWKZEXLJZEXDFULCRIRIZKYDVKZT),
(18, IXYVJYDWKIYDWCETKBQHQHYJXCUJYS),
(19, HWXUIXCVJHXCVBDSJAPGPGXIWBTIXR),
(20, GVWTHWBUIGWBUACRIZOFOFWHVASHWQ),
(21, FUVSGVATHFVATZBQHYNENEVGUZRGVP),
(22, ETURFUZSGEUZSYAPGXMDMDUFTYQFUO),
(23, DSTQETYRFDTYRXZOFWLCLCTESXPETN),
(24, CRSPDSXQECSXQWYNEVKBKBSDRWODSM),
(25, BQROCRWPDBRWPVXMDUJAJARCQVNCRL)]
Use the chi-square ranking function, i.e. ranking="chisquare":
sage: S.brute_force(C, ranking="chisquare")
<BLANKLINE>
[(8, SHIFTINGUSINGMODULARARITHMETIC),
(14, MBCZNCHAOMCHAGIXOFULULCNBGYNCW),
(20, GVWTHWBUIGWBUACRIZOFOFWHVASHWQ),
(13, NCDAODIBPNDIBHJYPGVMVMDOCHZODX),
(1, ZOPMAPUNBZPUNTVKBSHYHYPAOTLAPJ),
(23, DSTQETYRFDTYRXZOFWLCLCTESXPETN),
(10, QFGDRGLESQGLEKMBSJYPYPGRFKCRGA),
(6, UJKHVKPIWUKPIOQFWNCTCTKVJOGVKE),
(22, ETURFUZSGEUZSYAPGXMDMDUFTYQFUO),
(15, LABYMBGZNLBGZFHWNETKTKBMAFXMBV),
(12, ODEBPEJCQOEJCIKZQHWNWNEPDIAPEY),
(21, FUVSGVATHFVATZBQHYNENEVGUZRGVP),
(16, KZAXLAFYMKAFYEGVMDSJSJALZEWLAU),
(25, BQROCRWPDBRWPVXMDUJAJARCQVNCRL),
(9, RGHESHMFTRHMFLNCTKZQZQHSGLDSHB),
(24, CRSPDSXQECSXQWYNEVKBKBSDRWODSM),
(3, XMNKYNSLZXNSLRTIZQFWFWNYMRJYNH),
(5, VKLIWLQJXVLQJPRGXODUDULWKPHWLF),
(7, TIJGUJOHVTJOHNPEVMBSBSJUINFUJD),
(2, YNOLZOTMAYOTMSUJARGXGXOZNSKZOI),
(18, IXYVJYDWKIYDWCETKBQHQHYJXCUJYS),
(4, WLMJXMRKYWMRKQSHYPEVEVMXLQIXMG),
(11, PEFCQFKDRPFKDJLARIXOXOFQEJBQFZ),
(19, HWXUIXCVJHXCVBDSJAPGPGXIWBTIXR),
(0, APQNBQVOCAQVOUWLCTIZIZQBPUMBQK),
(17, JYZWKZEXLJZEXDFULCRIRIZKYDVKZT)]
Use the squared differences ranking function, i.e. ranking="squared_differences":
sage: S.brute_force(C, ranking="squared_differences")
<BLANKLINE>
[(8, SHIFTINGUSINGMODULARARITHMETIC),
(23, DSTQETYRFDTYRXZOFWLCLCTESXPETN),
(12, ODEBPEJCQOEJCIKZQHWNWNEPDIAPEY),
(2, YNOLZOTMAYOTMSUJARGXGXOZNSKZOI),
(9, RGHESHMFTRHMFLNCTKZQZQHSGLDSHB),
(7, TIJGUJOHVTJOHNPEVMBSBSJUINFUJD),
(21, FUVSGVATHFVATZBQHYNENEVGUZRGVP),
(22, ETURFUZSGEUZSYAPGXMDMDUFTYQFUO),
(1, ZOPMAPUNBZPUNTVKBSHYHYPAOTLAPJ),
(16, KZAXLAFYMKAFYEGVMDSJSJALZEWLAU),
(20, GVWTHWBUIGWBUACRIZOFOFWHVASHWQ),
(24, CRSPDSXQECSXQWYNEVKBKBSDRWODSM),
(14, MBCZNCHAOMCHAGIXOFULULCNBGYNCW),
(13, NCDAODIBPNDIBHJYPGVMVMDOCHZODX),
(3, XMNKYNSLZXNSLRTIZQFWFWNYMRJYNH),
(10, QFGDRGLESQGLEKMBSJYPYPGRFKCRGA),
(15, LABYMBGZNLBGZFHWNETKTKBMAFXMBV),
(6, UJKHVKPIWUKPIOQFWNCTCTKVJOGVKE),
(11, PEFCQFKDRPFKDJLARIXOXOFQEJBQFZ),
(25, BQROCRWPDBRWPVXMDUJAJARCQVNCRL),
(17, JYZWKZEXLJZEXDFULCRIRIZKYDVKZT),
(19, HWXUIXCVJHXCVBDSJAPGPGXIWBTIXR),
(4, WLMJXMRKYWMRKQSHYPEVEVMXLQIXMG),
(0, APQNBQVOCAQVOUWLCTIZIZQBPUMBQK),
(18, IXYVJYDWKIYDWCETKBQHQHYJXCUJYS),
(5, VKLIWLQJXVLQJPRGXODUDULWKPHWLF)]
TESTS:
Currently, the octal number system is not supported as an alphabet for this shift cryptosystem:
sage: SA = ShiftCryptosystem(AlphabeticStrings())
sage: OctStr = OctalStrings()
sage: C = OctStr([1, 2, 3])
sage: SA.brute_force(C)
...
TypeError: ciphertext must be encoded using one of the supported cipher domains of this shift cryptosystem.
Nor is the radix-64 alphabet supported:
sage: Rad64 = Radix64Strings()
sage: C = Rad64([1, 2, 3])
sage: SA.brute_force(C)
...
TypeError: ciphertext must be encoded using one of the supported cipher domains of this shift cryptosystem.
Decrypt the ciphertext C with the key K using shift cipher decryption.
INPUT:
 satisfying the inequality
satisfying the inequality
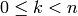 , where
, where  is the size of the cipher domain.
is the size of the cipher domain.OUTPUT:
EXAMPLES:
Let’s perform decryption over the supported alphabets. Here is decryption over the capital letters of the English alphabet:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: P = S.encoding("Stop shifting me."); P
STOPSHIFTINGME
sage: K = 13
sage: C = S.enciphering(K, P); C
FGBCFUVSGVATZR
sage: S.deciphering(K, C) == P
True
Decryption over the hexadecimal number system:
sage: S = ShiftCryptosystem(HexadecimalStrings())
sage: P = S.encoding("Shift me now."); P
5368696674206d65206e6f772e
sage: K = 7
sage: C = S.enciphering(K, P); C
cadfd0ddeb97d4dc97d5d6ee95
sage: S.deciphering(K, C) == P
True
Decryption over the binary number system:
sage: S = ShiftCryptosystem(BinaryStrings())
sage: P = S.encoding("OK, enough shifting."); P
0100111101001011001011000010000001100101011011100110111101110101011001110110100000100000011100110110100001101001011001100111010001101001011011100110011100101110
sage: K = 1
sage: C = S.enciphering(K, P); C
1011000010110100110100111101111110011010100100011001000010001010100110001001011111011111100011001001011110010110100110011000101110010110100100011001100011010001
sage: S.deciphering(K, C) == P
True
Encrypt the plaintext P with the key K using shift cipher encryption.
INPUT:
 satisfying the inequality
satisfying the inequality
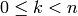 , where
, where  is the size of the cipher domain.
is the size of the cipher domain.OUTPUT:
EXAMPLES:
Let’s perform encryption over the supported alphabets. Here is encryption over the capital letters of the English alphabet:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: P = S.encoding("Shift your gear."); P
SHIFTYOURGEAR
sage: K = 3
sage: S.enciphering(K, P)
VKLIWBRXUJHDU
Encryption over the hexadecimal number system:
sage: S = ShiftCryptosystem(HexadecimalStrings())
sage: P = S.encoding("Capitalize with the shift key."); P
4361706974616c697a65207769746820746865207368696674206b65792e
sage: K = 5
sage: S.enciphering(K, P)
98b6c5bec9b6b1becfba75ccbec9bd75c9bdba75c8bdbebbc975b0bace73
Encryption over the binary number system:
sage: S = ShiftCryptosystem(BinaryStrings())
sage: P = S.encoding("Don't shift."); P
010001000110111101101110001001110111010000100000011100110110100001101001011001100111010000101110
sage: K = 1
sage: S.enciphering(K, P)
101110111001000010010001110110001000101111011111100011001001011110010110100110011000101111010001
The encoding of the string S over the string monoid of this shift cipher. For example, if the string monoid of this cryptosystem is AlphabeticStringMonoid, then the encoding of S would be its upper-case equivalent stripped of all non-alphabetic characters. The following alphabets are supported for the shift cipher:
INPUT:
OUTPUT:
EXAMPLES:
Encoding over the upper-case letters of the English alphabet:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: S.encoding("Shift cipher on capital letters of the English alphabet.")
SHIFTCIPHERONCAPITALLETTERSOFTHEENGLISHALPHABET
Encoding over the binary system:
sage: S = ShiftCryptosystem(BinaryStrings())
sage: S.encoding("Binary")
010000100110100101101110011000010111001001111001
Encoding over the hexadecimal system:
sage: S = ShiftCryptosystem(HexadecimalStrings())
sage: S.encoding("Over hexadecimal system.")
4f7665722068657861646563696d616c2073797374656d2e
The argument S can be an empty string, in which case an empty string is returned:
sage: ShiftCryptosystem(AlphabeticStrings()).encoding("")
<BLANKLINE>
sage: ShiftCryptosystem(HexadecimalStrings()).encoding("")
<BLANKLINE>
sage: ShiftCryptosystem(BinaryStrings()).encoding("")
<BLANKLINE>
The inverse key corresponding to the key K. For the shift cipher,
the inverse key corresponding to K is 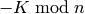 , where
, where
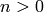 is the size of the cipher domain, i.e. the
plaintext/ciphertext space. A key
is the size of the cipher domain, i.e. the
plaintext/ciphertext space. A key  of the shift cipher is an
integer
of the shift cipher is an
integer 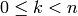 . The key
. The key 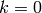 has no effect on either the
plaintext or the ciphertext.
has no effect on either the
plaintext or the ciphertext.
INPUT:
 such that
such that 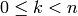 , where
, where  is the size of the cipher domain.
is the size of the cipher domain.OUTPUT:
EXAMPLES:
Some random keys and their respective inverse keys:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: key = S.random_key(); key # random
2
sage: S.inverse_key(key) # random
24
sage: S = ShiftCryptosystem(HexadecimalStrings())
sage: key = S.random_key(); key # random
12
sage: S.inverse_key(key) # random
4
sage: S = ShiftCryptosystem(BinaryStrings())
sage: key = S.random_key(); key # random
1
sage: S.inverse_key(key) # random
1
sage: key = S.random_key(); key # random
0
sage: S.inverse_key(key) # random
0
Regardless of the value of a key, the addition of the key and its inverse must be equal to the alphabet size. This relationship holds exactly when the value of the key is non-zero:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: K = S.random_key()
sage: while K == 0:
... K = S.random_key()
...
sage: invK = S.inverse_key(K)
sage: K + invK == S.alphabet_size()
True
sage: invK + K == S.alphabet_size()
True
sage: K = S.random_key()
sage: while K != 0:
... K = S.random_key()
...
sage: invK = S.inverse_key(K)
sage: K + invK != S.alphabet_size()
True
sage: K; invK
0
0
TESTS:
The key K must satisfy the inequality 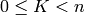 with
with  being the size of the plaintext, ciphertext, and key spaces. For the
shift cryptosystem, all these spaces are the same alphabet. This
inequality must be satisfied for each of the supported alphabets.
The capital letters of the English alphabet:
being the size of the plaintext, ciphertext, and key spaces. For the
shift cryptosystem, all these spaces are the same alphabet. This
inequality must be satisfied for each of the supported alphabets.
The capital letters of the English alphabet:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: S.inverse_key(S.alphabet_size())
...
ValueError: K (=26) is outside the range of acceptable values for a key of this shift cryptosystem.
sage: S.inverse_key(-1)
...
ValueError: K (=-1) is outside the range of acceptable values for a key of this shift cryptosystem.
The hexadecimal number system:
sage: S = ShiftCryptosystem(HexadecimalStrings())
sage: S.inverse_key(S.alphabet_size())
...
ValueError: K (=16) is outside the range of acceptable values for a key of this shift cryptosystem.
sage: S.inverse_key(-1)
...
ValueError: K (=-1) is outside the range of acceptable values for a key of this shift cryptosystem.
The binary number system:
sage: S = ShiftCryptosystem(BinaryStrings())
sage: S.inverse_key(S.alphabet_size())
...
ValueError: K (=2) is outside the range of acceptable values for a key of this shift cryptosystem.
sage: S.inverse_key(-1)
...
ValueError: K (=-1) is outside the range of acceptable values for a key of this shift cryptosystem.
Generate a random key within the key space of this shift cipher.
The generated key is an integer 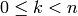 with
with  being the
size of the cipher domain. Thus there are
being the
size of the cipher domain. Thus there are  possible keys in the
key space, which is the set
possible keys in the
key space, which is the set 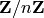 . The key
. The key 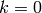 has no
effect on either the plaintext or the ciphertext.
has no
effect on either the plaintext or the ciphertext.
OUTPUT:
EXAMPLES:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: S.random_key() # random
18
sage: S = ShiftCryptosystem(BinaryStrings())
sage: S.random_key() # random
0
sage: S = ShiftCryptosystem(HexadecimalStrings())
sage: S.random_key() # random
5
Regardless of the value of a key, the addition of the key and its inverse must be equal to the alphabet size. This relationship holds exactly when the value of the key is non-zero:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: K = S.random_key()
sage: while K == 0:
... K = S.random_key()
...
sage: invK = S.inverse_key(K)
sage: K + invK == S.alphabet_size()
True
sage: invK + K == S.alphabet_size()
True
sage: K = S.random_key()
sage: while K != 0:
... K = S.random_key()
...
sage: invK = S.inverse_key(K)
sage: K + invK != S.alphabet_size()
True
sage: K; invK
0
0
Use the chi-square statistic to rank all possible keys. Currently, this method only applies to the capital letters of the English alphabet.
ALGORITHM:
Consider a non-empty alphabet  consisting of
consisting of  elements, and let
elements, and let  be a ciphertext encoded using elements of
be a ciphertext encoded using elements of
 . The plaintext
. The plaintext  corresponding to
corresponding to  is also encoded using
elements of
is also encoded using
elements of  . Let
. Let  be a candidate decipherment of
be a candidate decipherment of  ,
i.e.
,
i.e.  is the result of attempting to decrypt
is the result of attempting to decrypt  using a key
using a key
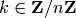 which is not necessarily the same key used to
encrypt
which is not necessarily the same key used to
encrypt  . Suppose
. Suppose 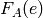 is the characteristic frequency
probability of
is the characteristic frequency
probability of 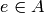 and let
and let 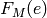 be the message frequency
probability with respect to
be the message frequency
probability with respect to  . The characteristic frequency
probability distribution of an alphabet is the expected frequency
probability distribution for that alphabet. The message frequency
probability distribution of
. The characteristic frequency
probability distribution of an alphabet is the expected frequency
probability distribution for that alphabet. The message frequency
probability distribution of  provides a distribution of the ratio
of character occurrences over message length. One can interpret the
characteristic frequency probability
provides a distribution of the ratio
of character occurrences over message length. One can interpret the
characteristic frequency probability 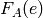 as the expected
probability, while the message frequency probability
as the expected
probability, while the message frequency probability 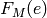 is
the observed probability. If
is
the observed probability. If  is of length
is of length  , then the observed
frequency of
, then the observed
frequency of 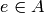 is
is
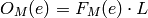
and the expected frequency of 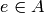 is
is
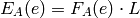
The chi-square rank 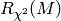 of
of  corresponding to a key
corresponding to a key
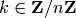 is given by
is given by
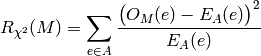
Cryptanalysis by exhaustive key search produces a candidate
decipherment 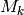 for each possible key
for each possible key 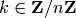 . For
a set
. For
a set
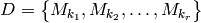 of all candidate decipherments corresponding to a ciphertext
of all candidate decipherments corresponding to a ciphertext  ,
the smaller is the rank
,
the smaller is the rank 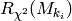 the more likely
that
the more likely
that 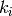 is the secret key. This key ranking method is based on
the Pearson chi-square test [PearsonTest09].
is the secret key. This key ranking method is based on
the Pearson chi-square test [PearsonTest09].
INPUT:
OUTPUT:
EXAMPLES:
Use the chi-square statistic to rank all possible keys and their corresponding decipherment:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: P = S.encoding("Shi."); P
SHI
sage: K = 5
sage: C = S.enciphering(K, P)
sage: Pdict = S.brute_force(C)
sage: S.rank_by_chi_square(C, Pdict)
<BLANKLINE>
[(9, ODE),
(5, SHI),
(20, DST),
(19, ETU),
(21, CRS),
(10, NCD),
(25, YNO),
(6, RGH),
(12, LAB),
(8, PEF),
(1, WLM),
(11, MBC),
(18, FUV),
(17, GVW),
(2, VKL),
(4, TIJ),
(3, UJK),
(0, XMN),
(16, HWX),
(15, IXY),
(23, APQ),
(24, ZOP),
(22, BQR),
(7, QFG),
(13, KZA),
(14, JYZ)]
As more ciphertext is available, the reliability of the chi-square ranking function increases:
sage: P = S.encoding("Shift cipher."); P
SHIFTCIPHER
sage: C = S.enciphering(K, P)
sage: Pdict = S.brute_force(C)
sage: S.rank_by_chi_square(C, Pdict)
<BLANKLINE>
[(5, SHIFTCIPHER),
(9, ODEBPYELDAN),
(18, FUVSGPVCURE),
(2, VKLIWFLSKHU),
(20, DSTQENTASPC),
(19, ETURFOUBTQD),
(21, CRSPDMSZROB),
(6, RGHESBHOGDQ),
(7, QFGDRAGNFCP),
(12, LABYMVBIAXK),
(17, GVWTHQWDVSF),
(24, ZOPMAJPWOLY),
(1, WLMJXGMTLIV),
(0, XMNKYHNUMJW),
(11, MBCZNWCJBYL),
(8, PEFCQZFMEBO),
(25, YNOLZIOVNKX),
(10, NCDAOXDKCZM),
(3, UJKHVEKRJGT),
(4, TIJGUDJQIFS),
(22, BQROCLRYQNA),
(16, HWXUIRXEWTG),
(15, IXYVJSYFXUH),
(14, JYZWKTZGYVI),
(13, KZAXLUAHZWJ),
(23, APQNBKQXPMZ)]
TESTS:
The ciphertext cannot be an empty string:
sage: S.rank_by_chi_square("", Pdict)
...
AttributeError: 'str' object has no attribute 'parent'
sage: S.rank_by_chi_square(S.encoding(""), Pdict)
...
ValueError: The ciphertext must be a non-empty string.
sage: S.rank_by_chi_square(S.encoding(" "), Pdict)
...
ValueError: The ciphertext must be a non-empty string.
The ciphertext must be encoded using the capital letters of the English alphabet as implemented in AlphabeticStrings():
sage: H = HexadecimalStrings()
sage: S.rank_by_chi_square(H.encoding("shift"), Pdict)
...
TypeError: The ciphertext must be capital letters of the English alphabet.
sage: B = BinaryStrings()
sage: S.rank_by_chi_square(B.encoding("shift"), Pdict)
...
TypeError: The ciphertext must be capital letters of the English alphabet.
The dictionary pdict cannot be empty:
sage: S.rank_by_chi_square(C, {})
...
KeyError: 0
REFERENCES:
| [PearsonTest09] | (1, 2) Pearson chi-square test. Wikipedia, accessed 13th October 2009. |
Use the squared-differences measure to rank all possible keys. Currently, this method only applies to the capital letters of the English alphabet.
ALGORITHM:
Consider a non-empty alphabet  consisting of
consisting of  elements, and let
elements, and let  be a ciphertext encoded using elements of
be a ciphertext encoded using elements of
 . The plaintext
. The plaintext  corresponding to
corresponding to  is also encoded using
elements of
is also encoded using
elements of  . Let
. Let  be a candidate decipherment of
be a candidate decipherment of  ,
i.e.
,
i.e.  is the result of attempting to decrypt
is the result of attempting to decrypt  using a key
using a key
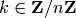 which is not necessarily the same key used to
encrypt
which is not necessarily the same key used to
encrypt  . Suppose
. Suppose 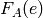 is the characteristic frequency
probability of
is the characteristic frequency
probability of 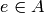 and let
and let 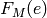 be the message
frequency probability with respect to
be the message
frequency probability with respect to  . The characteristic
frequency probability distribution of an alphabet is the expected
frequency probability distribution for that alphabet. The message
frequency probability distribution of
. The characteristic
frequency probability distribution of an alphabet is the expected
frequency probability distribution for that alphabet. The message
frequency probability distribution of  provides a distribution
of the ratio of character occurrences over message length. One can
interpret the characteristic frequency probability
provides a distribution
of the ratio of character occurrences over message length. One can
interpret the characteristic frequency probability 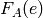 as the
expected probability, while the message frequency probability
as the
expected probability, while the message frequency probability
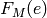 is the observed probability. If
is the observed probability. If  is of length
is of length  , then
the observed frequency of
, then
the observed frequency of 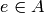 is
is
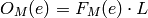
and the expected frequency of 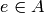 is
is
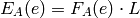
The squared-differences, or residual sum of squares, rank
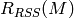 of
of  corresponding to a key
corresponding to a key
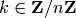 is given by
is given by
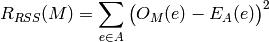
Cryptanalysis by exhaustive key search produces a candidate
decipherment 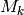 for each possible key
for each possible key 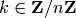 . For
a set
. For
a set
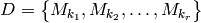 of all candidate decipherments corresponding to a ciphertext
of all candidate decipherments corresponding to a ciphertext  ,
the smaller is the rank
,
the smaller is the rank 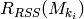 the more likely
that
the more likely
that 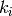 is the secret key. This key ranking method is based
on the residual sum of squares measure [RSS09].
is the secret key. This key ranking method is based
on the residual sum of squares measure [RSS09].
INPUT:
OUTPUT:
EXAMPLES:
Use the method of squared differences to rank all possible keys and their corresponding decipherment:
sage: S = ShiftCryptosystem(AlphabeticStrings())
sage: P = S.encoding("Shi."); P
SHI
sage: K = 5
sage: C = S.enciphering(K, P)
sage: Pdict = S.brute_force(C)
sage: S.rank_by_squared_differences(C, Pdict)
<BLANKLINE>
[(19, ETU),
(9, ODE),
(20, DST),
(5, SHI),
(8, PEF),
(4, TIJ),
(25, YNO),
(21, CRS),
(6, RGH),
(10, NCD),
(12, LAB),
(23, APQ),
(24, ZOP),
(0, XMN),
(13, KZA),
(15, IXY),
(1, WLM),
(16, HWX),
(22, BQR),
(11, MBC),
(18, FUV),
(2, VKL),
(17, GVW),
(7, QFG),
(3, UJK),
(14, JYZ)]
As more ciphertext is available, the reliability of the squared differences ranking function increases:
sage: P = S.encoding("Shift cipher."); P
SHIFTCIPHER
sage: C = S.enciphering(K, P)
sage: Pdict = S.brute_force(C)
sage: S.rank_by_squared_differences(C, Pdict)
<BLANKLINE>
[(20, DSTQENTASPC),
(5, SHIFTCIPHER),
(9, ODEBPYELDAN),
(19, ETURFOUBTQD),
(6, RGHESBHOGDQ),
(16, HWXUIRXEWTG),
(8, PEFCQZFMEBO),
(21, CRSPDMSZROB),
(22, BQROCLRYQNA),
(25, YNOLZIOVNKX),
(3, UJKHVEKRJGT),
(18, FUVSGPVCURE),
(4, TIJGUDJQIFS),
(10, NCDAOXDKCZM),
(7, QFGDRAGNFCP),
(24, ZOPMAJPWOLY),
(2, VKLIWFLSKHU),
(12, LABYMVBIAXK),
(17, GVWTHQWDVSF),
(1, WLMJXGMTLIV),
(13, KZAXLUAHZWJ),
(0, XMNKYHNUMJW),
(15, IXYVJSYFXUH),
(14, JYZWKTZGYVI),
(11, MBCZNWCJBYL),
(23, APQNBKQXPMZ)]
TESTS:
The ciphertext cannot be an empty string:
sage: S.rank_by_squared_differences("", Pdict)
...
AttributeError: 'str' object has no attribute 'parent'
sage: S.rank_by_squared_differences(S.encoding(""), Pdict)
...
ValueError: The ciphertext must be a non-empty string.
sage: S.rank_by_squared_differences(S.encoding(" "), Pdict)
...
ValueError: The ciphertext must be a non-empty string.
The ciphertext must be encoded using the capital letters of the English alphabet as implemented in AlphabeticStrings():
sage: H = HexadecimalStrings()
sage: S.rank_by_squared_differences(H.encoding("shift"), Pdict)
...
TypeError: The ciphertext must be capital letters of the English alphabet.
sage: B = BinaryStrings()
sage: S.rank_by_squared_differences(B.encoding("shift"), Pdict)
...
TypeError: The ciphertext must be capital letters of the English alphabet.
The dictionary pdict cannot be empty:
sage: S.rank_by_squared_differences(C, {})
...
KeyError: 0
REFERENCES:
| [RSS09] | (1, 2) Residual sum of squares. Wikipedia, accessed 13th October 2009. |
Bases: sage.crypto.cryptosystem.SymmetricKeyCryptosystem
Create a substitution cryptosystem.
INPUT:
OUTPUT:
EXAMPLES:
sage: M = AlphabeticStrings()
sage: E = SubstitutionCryptosystem(M)
sage: E
Substitution cryptosystem on Free alphabetic string monoid on A-Z
sage: K = M([ 25-i for i in range(26) ])
sage: K
ZYXWVUTSRQPONMLKJIHGFEDCBA
sage: e = E(K)
sage: m = M("THECATINTHEHAT")
sage: e(m)
GSVXZGRMGSVSZG
TESTS:
sage: M = AlphabeticStrings()
sage: E = SubstitutionCryptosystem(M)
sage: E == loads(dumps(E))
True
Decrypt the ciphertext C using the key K.
INPUT:
OUTPUT:
EXAMPLES:
sage: S = SubstitutionCryptosystem(AlphabeticStrings())
sage: K = S.random_key()
sage: M = S.encoding("Don't substitute me!")
sage: S.deciphering(K, S.enciphering(K, M)) == M
True
Encrypt the plaintext M using the key K.
INPUT:
OUTPUT:
EXAMPLES:
sage: S = SubstitutionCryptosystem(AlphabeticStrings())
sage: K = S.random_key()
sage: M = S.encoding("Don't substitute me.")
sage: S.deciphering(K, S.enciphering(K, M)) == M
True
The encoding of the string M over the string monoid of this substitution cipher. For example, if the string monoid of this cryptosystem is AlphabeticStringMonoid, then the encoding of M would be its upper-case equivalent stripped of all non-alphabetic characters.
INPUT:
OUTPUT:
EXAMPLES:
sage: M = "Peter Pan(ning) for gold."
sage: A = AlphabeticStrings()
sage: S = SubstitutionCryptosystem(A)
sage: S.encoding(M) == A.encoding(M)
True
The inverse key corresponding to the key K. The specified key is a permutation of the cryptosystem alphabet.
INPUT:
OUTPUT:
EXAMPLES:
sage: S = AlphabeticStrings()
sage: E = SubstitutionCryptosystem(S)
sage: K = E.random_key()
sage: L = E.inverse_key(K)
sage: M = S("THECATINTHEHAT")
sage: e = E(K)
sage: c = E(L)
sage: c(e(M))
THECATINTHEHAT
Generate a random key within the key space of this substitution
cipher. The generated key is a permutation of the cryptosystem
alphabet. Let  be the length of the alphabet. Then there are
be the length of the alphabet. Then there are
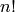 possible keys in the key space.
possible keys in the key space.
OUTPUT:
EXAMPLES:
sage: A = AlphabeticStrings()
sage: S = SubstitutionCryptosystem(A)
sage: K = S.random_key()
sage: Ki = S.inverse_key(K)
sage: M = "THECATINTHEHAT"
sage: e = S(K)
sage: d = S(Ki)
sage: d(e(A(M))) == A(M)
True
Bases: sage.crypto.cryptosystem.SymmetricKeyCryptosystem
Create a transposition cryptosystem of block length n.
INPUT:
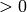 ; a block length of a block permutation
; a block length of a block permutationOUTPUT:
EXAMPLES:
sage: S = AlphabeticStrings()
sage: E = TranspositionCryptosystem(S,14)
sage: E
Transposition cryptosystem on Free alphabetic string monoid on A-Z of block length 14
sage: K = [ 14-i for i in range(14) ]
sage: K
[14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
sage: e = E(K)
sage: e(S("THECATINTHEHAT"))
TAHEHTNITACEHT
TESTS:
sage: S = AlphabeticStrings()
sage: E = TranspositionCryptosystem(S,14)
sage: E == loads(dumps(E))
True
Decrypt the ciphertext C using the key K.
INPUT:
OUTPUT:
EXAMPLES:
sage: T = TranspositionCryptosystem(AlphabeticStrings(), 14)
sage: K = T.random_key()
sage: M = T.encoding("The cat in the hat.")
sage: T.deciphering(K, T.enciphering(K, M)) == M
True
Encrypt the plaintext M using the key K.
INPUT:
OUTPUT:
EXAMPLES:
sage: T = TranspositionCryptosystem(AlphabeticStrings(), 14)
sage: K = T.random_key()
sage: M = T.encoding("The cat in the hat.")
sage: T.deciphering(K, T.enciphering(K, M)) == M
True
The encoding of the string M over the string monoid of this transposition cipher. For example, if the string monoid of this cryptosystem is AlphabeticStringMonoid, then the encoding of M would be its upper-case equivalent stripped of all non-alphabetic characters.
INPUT:
OUTPUT:
EXAMPLES:
sage: M = "Transposition cipher is not about matrix transpose."
sage: A = AlphabeticStrings()
sage: T = TranspositionCryptosystem(A, 11)
sage: T.encoding(M) == A.encoding(M)
True
The inverse key corresponding to the key K.
INPUT:
OUTPUT:
EXAMPLES:
sage: S = AlphabeticStrings()
sage: E = TranspositionCryptosystem(S, 14)
sage: K = E.random_key()
sage: Ki = E.inverse_key(K)
sage: e = E(K)
sage: d = E(Ki)
sage: M = "THECATINTHEHAT"
sage: C = e(S(M))
sage: d(S(C)) == S(M)
True
Generate a random key within the key space of this transposition
cryptosystem. Let 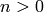 be the block length of this cryptosystem.
Then there are
be the block length of this cryptosystem.
Then there are 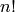 possible keys.
possible keys.
OUTPUT:
EXAMPLES:
sage: S = AlphabeticStrings()
sage: E = TranspositionCryptosystem(S, 14)
sage: K = E.random_key()
sage: Ki = E.inverse_key(K)
sage: e = E(K)
sage: d = E(Ki)
sage: M = "THECATINTHEHAT"
sage: C = e(S(M))
sage: d(S(C)) == S(M)
True
Bases: sage.crypto.cryptosystem.SymmetricKeyCryptosystem
Create a Vigenere cryptosystem of block length n.
INPUT:
 ; block length of an encryption/decryption key
; block length of an encryption/decryption keyOUTPUT:
EXAMPLES:
sage: S = AlphabeticStrings()
sage: E = VigenereCryptosystem(S,14)
sage: E
Vigenere cryptosystem on Free alphabetic string monoid on A-Z of period 14
sage: K = S('ABCDEFGHIJKLMN')
sage: K
ABCDEFGHIJKLMN
sage: e = E(K)
sage: e
Cipher on Free alphabetic string monoid on A-Z
sage: e(S("THECATINTHEHAT"))
TIGFEYOUBQOSMG
TESTS:
sage: S = AlphabeticStrings()
sage: E = VigenereCryptosystem(S,14)
sage: E == loads(dumps(E))
True
Decrypt the ciphertext C using the key K.
INPUT:
OUTPUT:
EXAMPLES:
sage: V = VigenereCryptosystem(AlphabeticStrings(), 24)
sage: K = V.random_key()
sage: M = V.encoding("Jack and Jill went up the hill.")
sage: V.deciphering(K, V.enciphering(K, M)) == M
True
Encrypt the plaintext M using the key K.
INPUT:
OUTPUT:
EXAMPLES:
sage: V = VigenereCryptosystem(AlphabeticStrings(), 24)
sage: K = V.random_key()
sage: M = V.encoding("Jack and Jill went up the hill.")
sage: V.deciphering(K, V.enciphering(K, M)) == M
True
The encoding of the string M over the string monoid of this Vigenere cipher. For example, if the string monoid of this cryptosystem is AlphabeticStringMonoid, then the encoding of M would be its upper-case equivalent stripped of all non-alphabetic characters.
INPUT:
OUTPUT:
EXAMPLES:
sage: A = AlphabeticStrings()
sage: V = VigenereCryptosystem(A, 24)
sage: M = "Jack and Jill went up the hill."
sage: V.encoding(M) == A.encoding(M)
True
The inverse key corresponding to the key K.
INPUT:
OUTPUT:
EXAMPLES:
sage: S = AlphabeticStrings()
sage: E = VigenereCryptosystem(S,14)
sage: K = E.random_key()
sage: L = E.inverse_key(K)
sage: M = S("THECATINTHEHAT")
sage: e = E(K)
sage: c = E(L)
sage: c(e(M))
THECATINTHEHAT
Generate a random key within the key space of this Vigenere
cryptosystem. Let  be the length of the cryptosystem alphabet
and let
be the length of the cryptosystem alphabet
and let 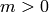 be the block length of this cryptosystem. Then there
are
be the block length of this cryptosystem. Then there
are 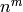 possible keys.
possible keys.
OUTPUT:
EXAMPLES:
sage: A = AlphabeticStrings()
sage: V = VigenereCryptosystem(A, 14)
sage: M = "THECATINTHEHAT"
sage: K = V.random_key()
sage: Ki = V.inverse_key(K)
sage: e = V(K)
sage: d = V(Ki)
sage: d(e(A(M))) == A(M)
True