Suffix Tries and Suffix Trees¶

class sage.combinat.words.suffix_trees.ImplicitSuffixTree(word)¶

Bases: sage.structure.sage_object.SageObject

active_state()¶

Returns the active state of the suffix tree.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: W = Words([0,1,2])
sage: t = ImplicitSuffixTree(W([0,1,0,1,2]))
sage: t.active_state()
(0, (6, 6))

edge_iterator()¶

Returns an iterator over the edges of the suffix tree. The edge from $u$ to $v$ labelled by 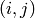$(i,j)$ is returned as the tuple $(u,v,(i,j))$ .

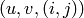EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: sorted( ImplicitSuffixTree(Word("aaaaa")).edge_iterator() )
[(0, 1, (0, None))]
sage: sorted( ImplicitSuffixTree(Word([0,1,0,1])).edge_iterator() )
[(0, 1, (0, None)), (0, 2, (1, None))]
sage: sorted( ImplicitSuffixTree(Word()).edge_iterator() )
[]

factor_iterator(n=None)¶

Generate distinct factors of self.

INPUT:

n - an integer, or None.

OUTPUT:

If n is an integer, returns an iterator over all distinct factors of length n. If n is None, returns an iterator generating all distinct factors.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: sorted( ImplicitSuffixTree(Word("cacao")).factor_iterator() )
[word: , word: a, word: ac, word: aca, word: acao, word: ao, word: c, word: ca, word: cac, word: caca, word: cacao, word: cao, word: o]
sage: sorted( ImplicitSuffixTree(Word("cacao")).factor_iterator(1) )
[word: a, word: c, word: o]
sage: sorted( ImplicitSuffixTree(Word("cacao")).factor_iterator(2) )
[word: ac, word: ao, word: ca]
sage: sorted( ImplicitSuffixTree(Word([0,0,0])).factor_iterator() )
[word: , word: 0, word: 00, word: 000]
sage: sorted( ImplicitSuffixTree(Word([0,0,0])).factor_iterator(2) )
[word: 00]
sage: sorted( ImplicitSuffixTree(Word([0,0,0])).factor_iterator(0) )
[word: ]
sage: sorted( ImplicitSuffixTree(Word()).factor_iterator() )
[word: ]
sage: sorted( ImplicitSuffixTree(Word()).factor_iterator(2) )
[]

number_of_factors(n=None)¶

Count the number of distinct factors of self.word().

INPUT:

n - an integer, or None.

OUTPUT:

If n is an integer, returns the number of distinct factors of length n. If n is None, returns the total number of distinct factors.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: t = ImplicitSuffixTree(Word([1,2,1,3,1,2,1]))
sage: t.number_of_factors()
22
sage: t.number_of_factors(1)
3
sage: t.number_of_factors(9)
0
sage: t.number_of_factors(0)
1

sage: t = ImplicitSuffixTree(Word("cacao"))
sage: t.number_of_factors()
13
sage: map(t.number_of_factors, range(10))
[1, 3, 3, 3, 2, 1, 0, 0, 0, 0]

sage: t = ImplicitSuffixTree(Word("c"*1000))
sage: t.number_of_factors()
1001
sage: t.number_of_factors(17)
1
sage: t.number_of_factors(0)
1

sage: ImplicitSuffixTree(Word()).number_of_factors()
1

sage: blueberry = ImplicitSuffixTree(Word("blueberry"))
sage: blueberry.number_of_factors()
43
sage: map(blueberry.number_of_factors, range(10))
[1, 6, 8, 7, 6, 5, 4, 3, 2, 1]

plot(word_labels=False, layout='tree', tree_root=0, tree_orientation='up', vertex_colors=None, edge_labels=True, *args, **kwds)¶

Returns a Graphics object corresponding to the transition graph of the suffix tree.

INPUT:

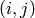word_labels - boolean (defaut: False) if False, labels the edges by pairs $(i, j)$ ; if True, labels the edges by word[i:j].
layout - (defaut: 'tree')
tree_root - (defaut: 0)
tree_orientation - (defaut: 'up')
vertex_colors - (defaut: None)
edge_labels - (defaut: True)

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: ImplicitSuffixTree(Word('cacao')).plot(word_labels=True)
sage: ImplicitSuffixTree(Word('cacao')).plot(word_labels=False)

TESTS:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: type(ImplicitSuffixTree(Word('cacao')).plot(word_labels=True))
<class 'sage.plot.plot.Graphics'>
sage: type(ImplicitSuffixTree(Word('cacao')).plot(word_labels=False))
<class 'sage.plot.plot.Graphics'>

process_letter(letter)¶

Modifies the current implicit suffix tree producing the implicit suffix tree for self.word() + letter.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: w = Words("aco")("cacao")
sage: t = ImplicitSuffixTree(w[:-1]); t
Implicit Suffix Tree of the word: caca
sage: t.process_letter(w[-1]); t
Implicit Suffix Tree of the word: cacao

sage: W = Words([0,1])
sage: s = ImplicitSuffixTree(W([0,1,0,1])); s
Implicit Suffix Tree of the word: 0101
sage: s.process_letter(W([1])[0]); s
Implicit Suffix Tree of the word: 01011

show(word_labels=None, *args, **kwds)¶

Displays the output of self.plot().

INPUT:

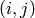word_labels - (default: None) if False, labels the edges by pairs $(i, j)$ ; if True, labels the edges by word[i:j].

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: w = Words("cao")("cacao")
sage: t = ImplicitSuffixTree(w)
sage: t.show(word_labels=True)
sage: t.show(word_labels=False)

states()¶

Returns the states (explicit nodes) of the suffix tree.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: W = Words([0,1,2])
sage: t = ImplicitSuffixTree(W([0,1,0,1,2]))
sage: t.states()
[0, 1, 2, 3, 4, 5, 6, 7]

suffix_link(state)¶

Evaluates the suffix link map of the implicit suffix tree on state. Note that the suffix link is not defined for all states.

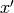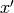The suffix link of a state $x'$ that corresponds to the suffix $x$ is defined to be -1 is $x'$ is the root (0) and 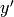$y'$ otherwise, where 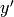$y'$ is the state corresponding to the suffix x[1:].

INPUT:

state - a state

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: W = Words([0,1,2])
sage: t = ImplicitSuffixTree(W([0,1,0,1,2]))
sage: t.suffix_link(3)
5
sage: t.suffix_link(5)
0
sage: t.suffix_link(0)
-1
sage: t.suffix_link(-1)
Traceback (most recent call last):
    ...
TypeError: there is no suffix link from -1

to_digraph(word_labels=False)¶

Returns a DiGraph object of the transition graph of the suffix tree.

INPUT:

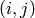word_labels - boolean (defaut: False) if False, labels the edges by pairs $(i, j)$ ; if True, labels the edges by word[i:j].

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: W = Words([0,1,2])
sage: t = ImplicitSuffixTree(W([0,1,0,1,2]))
sage: t.to_digraph()
Digraph on 8 vertices

to_explicit_suffix_tree()¶

Converts self to an explicit suffix tree. It is obtained by processing an end of string letter as if it were a regular letter, except that no new leaf nodes are created (thus, the only thing that happens is that some implicit nodes become explicit).

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: w = Words("aco")("cacao")
sage: t = ImplicitSuffixTree(w)
sage: t.to_explicit_suffix_tree()

sage: W = Words([0,1])
sage: s = ImplicitSuffixTree(W([0,1,0,1,1]))
sage: s.to_explicit_suffix_tree()

transition_function(word, node=0)¶

Returns the node obtained by starting from node and following the edges labelled by the letters of word. Returns ("explicit", end_node) if we end at end_node, or ("implicit", (edge, d)) if we end $d$ spots along an edge.

INPUT:

word - a word
node - (default: 0) starting node

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: W = Words([0,1,2])
sage: t = ImplicitSuffixTree(W([0,1,0,1,2]))
sage: t.transition_function(W([0,1,0]))
('implicit', (3, 1), 1)
sage: t.transition_function(W([0,1,2]))
('explicit', 4)
sage: t.transition_function(W([0,1,2]), 5)
('explicit', 2)
sage: t.transition_function(W([0,1]), 5)
('implicit', (5, 2), 2)

transition_function_dictionary()¶

Returns the transition function as a dictionary of dictionaries. The format is consistent with the input format for DiGraph.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: W = Words("aco")
sage: t = ImplicitSuffixTree(W("cac"))
sage: t.transition_function_dictionary()
{0: {1: (0, None), 2: (1, None)}}

sage: W = Words([0,1])
sage: t = ImplicitSuffixTree(W([0,1,0]))
sage: t.transition_function_dictionary()
{0: {1: (0, None), 2: (1, None)}}

trie_type_dict()¶

Returns a dictionary in a format compatible with that of the suffix trie transition function.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree, SuffixTrie
sage: W = Words("ab")
sage: t = ImplicitSuffixTree(W("aba"))
sage: t.trie_type_dict() == dict([[(0, W("a")), 4], [(0, W("b")), 3], [(3, W("a")), 2], [(4, W("b")), 5], [(5, W("a")), 1]])
True

uncompactify()¶

Returns the tree obtained from self by splitting edges so that they are labelled by exactly one letter. The resulting tree is isomorphic to the suffix trie.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree, SuffixTrie
sage: abbab = Words("ab")("abbab")
sage: s = SuffixTrie(abbab)
sage: t = ImplicitSuffixTree(abbab)
sage: t.uncompactify().is_isomorphic(s.to_digraph())
True

word()¶

Returns the word whose implicit suffix tree this is.

TESTS:

sage: from sage.combinat.words.suffix_trees import ImplicitSuffixTree
sage: ImplicitSuffixTree(Word([0,1,0,1,0])).word() == Word([0,1,0,1,0])
True

class sage.combinat.words.suffix_trees.SuffixTrie(word)¶

Bases: sage.structure.sage_object.SageObject

active_state()¶

Returns the active state of the suffix trie. This is the state corresponding to the word as a suffix of itself.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("cao")("cacao")
sage: t = SuffixTrie(w)
sage: t.active_state()
8

sage: u = Words([0,1])([0,1,1,0,1,0,0,1])
sage: s = SuffixTrie(u)
sage: s.active_state()
22

final_states()¶

Returns the set of final states of the suffix trie. These are the states corresponding to the suffixes of self.word(). They are obtained be repeatedly following the suffix link from the active state until we reach 0.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("cao")("cacao")
sage: t = SuffixTrie(w)
sage: t.final_states() == Set([8, 9, 10, 11, 12, 0])
True

has_suffix(word)¶

Return True if and only if word is a suffix of self.word().

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("cao")("cacao")
sage: t = SuffixTrie(w)
sage: [t.has_suffix(w[i:]) for i in range(w.length()+1)]
[True, True, True, True, True, True]
sage: [t.has_suffix(w[:i]) for i in range(w.length()+1)]
[True, False, False, False, False, True]

node_to_word(state=0)¶

Returns the word obtained by reading the edge labels from 0 to state.

INPUT:

state - (default: 0) a state

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("abc")("abcba")
sage: t = SuffixTrie(w)
sage: t.node_to_word(10)
word: abcba
sage: t.node_to_word(7)
word: abcb

plot(layout='tree', tree_root=0, tree_orientation='up', vertex_colors=None, edge_labels=True, *args, **kwds)¶

Returns a Graphics object corresponding to the transition graph of the suffix trie.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: SuffixTrie(Word("cacao")).plot()

TESTS:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: type(SuffixTrie(Word("cacao")).plot())
<class 'sage.plot.plot.Graphics'>

process_letter(letter)¶

Modify self to produce the suffix trie for self.word() + letter.

Note

letter must occur within the alphabet of the word.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("ab")("ababba")
sage: t = SuffixTrie(w); t
Suffix Trie of the word: ababba
sage: t.process_letter("a"); t
Suffix Trie of the word: ababbaa

TESTS:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("cao")("cacao")
sage: t = SuffixTrie(w); t
Suffix Trie of the word: cacao
sage: t.process_letter("d")
...
ValueError: d not in alphabet!

show(*args, **kwds)¶

Displays the output of self.plot().

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("cao")("cac")
sage: t = SuffixTrie(w)
sage: t.show()

states()¶

Returns the states of the automaton defined by the suffix trie.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words([0,1])([0,1,1])
sage: t = SuffixTrie(w)
sage: t.states()
[0, 1, 2, 3, 4]

sage: u = Words("aco")("cacao")
sage: s = SuffixTrie(u)
sage: s.states()
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]

suffix_link(state)¶

Evaluates the suffix link map of the suffix trie on state. Note that the suffix link map is not defined on -1.

INPUT:

state - a state

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("cao")("cacao")
sage: t = SuffixTrie(w)
sage: map(t.suffix_link, range(13))
[-1, 0, 3, 0, 5, 1, 7, 2, 9, 10, 11, 12, 0]
sage: t.suffix_link(0)
-1

TESTS:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("cao")("cacao")
sage: t = SuffixTrie(w)
sage: t.suffix_link([1])
...
TypeError: [1] is not an integer
sage: t.suffix_link(-1)
...
TypeError: suffix link is not defined for -1
sage: t.suffix_link(17)
...
TypeError: 17 is not a state

to_digraph()¶

Returns a DiGraph object of the transition graph of the suffix trie.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("cao")("cac")
sage: t = SuffixTrie(w)
sage: d = t.to_digraph(); d
Digraph on 6 vertices
sage: d.adjacency_matrix()
[0 1 0 1 0 0]
[0 0 1 0 0 0]
[0 0 0 0 1 0]
[0 0 0 0 0 1]
[0 0 0 0 0 0]
[0 0 0 0 0 0]

transition_function(node, word)¶

Returns the state reached by beginning at node and following the arrows in the transition graph labelled by the letters of word.

INPUT:

node - a node
word - a word

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words([0,1])([0,1,0,1,1])
sage: t = SuffixTrie(w)
sage: [t.transition_function(u,letter) == v \
        for ((u,letter),v) in t._transition_function.iteritems()] \
        == [True] * len(t._transition_function)
True

word()¶

Returns the word whose suffix tree this is.

EXAMPLES:

sage: from sage.combinat.words.suffix_trees import SuffixTrie
sage: w = Words("abc")("abcba")
sage: t = SuffixTrie(w)
sage: t.word()
word: abcba
sage: t.word() == w
True

Suffix Tries and Suffix Trees¶

Previous topic

Next topic

This Page

Navigation

Suffix Tries and Suffix Trees¶

Previous topic

Next topic

This Page

Quick search

Navigation