Symmetric Group Algebra¶

sage.combinat.symmetric_group_algebra.HeckeAlgebraSymmetricGroupT(R, n, q=None)¶

Returns the Hecke algebra of the symmetric group on the T basis.

EXAMPLES:

sage: HeckeAlgebraSymmetricGroupT(QQ, 3)
Hecke algebra of the symmetric group of order 3 on the T basis over Univariate Polynomial Ring in q over Rational Field

sage: HeckeAlgebraSymmetricGroupT(QQ, 3, 2)
Hecke algebra of the symmetric group of order 3 with q=2 on the T basis over Rational Field

class sage.combinat.symmetric_group_algebra.HeckeAlgebraSymmetricGroup_generic(R, n, q=None)¶

Bases: sage.combinat.combinatorial_algebra.CombinatorialAlgebra

q()¶

EXAMPLES:

sage: HeckeAlgebraSymmetricGroupT(QQ, 3).q()
q
sage: HeckeAlgebraSymmetricGroupT(QQ, 3, 2).q()
2

class sage.combinat.symmetric_group_algebra.HeckeAlgebraSymmetricGroup_t(R, n, q=None)¶

Bases: sage.combinat.symmetric_group_algebra.HeckeAlgebraSymmetricGroup_generic

algebra_generators()¶

Return the generators of the algebra.

EXAMPLES:

sage: HeckeAlgebraSymmetricGroupT(QQ,3).algebra_generators()
[T[2, 1, 3], T[1, 3, 2]]

jucys_murphy(k)¶

Returns the Jucys-Murphy element J_k of the Hecke algebra. The Jucys-Murphy elements generate the maximal commutative sub-algebra of the Hecke algebra.

EXAMPLES:

sage: H3 = HeckeAlgebraSymmetricGroupT(QQ,3)
sage: j2 = H3.jucys_murphy(2); j2
q*T[1, 2, 3] + (q-1)*T[2, 1, 3]
sage: j3 = H3.jucys_murphy(3); j3 #################### SEGFAULTS ################
q^2*T[1, 2, 3] + (q^2-q)*T[1, 3, 2] + (q-1)*T[3, 2, 1]
sage: j2*j3 == j3*j2
True
sage: H3.jucys_murphy(1)
...
ValueError: k must be between 2 and n (= 3)

t(i)¶

EXAMPLES:

sage: H3 = HeckeAlgebraSymmetricGroupT(QQ,3)
sage: H3.t(1)
T[2, 1, 3]
sage: H3.t(2)
T[1, 3, 2]
sage: H3.t(0)
...
ValueError: i must be between 1 and n-1 (= 2)

t_action(a, i)¶

Return the action of T_i on a.

EXAMPLES:

sage: H3 = HeckeAlgebraSymmetricGroupT(QQ, 3)
sage: a = H3([2,1,3])+2*H3([1,2,3])
sage: H3.t_action(a, 1)
q*T[1, 2, 3] + (q+1)*T[2, 1, 3]
sage: H3.t(1)*a
q*T[1, 2, 3] + (q+1)*T[2, 1, 3]

t_action_on_basis(perm, i)¶

EXAMPLES:

sage: H3 = HeckeAlgebraSymmetricGroupT(QQ, 3)
sage: H3.t_action_on_basis(Permutation([2,1,3]), 1)
q*T[1, 2, 3] + (q-1)*T[2, 1, 3]
sage: H3.t_action_on_basis(Permutation([1,2,3]), 1)
T[2, 1, 3]
sage: H3 = HeckeAlgebraSymmetricGroupT(QQ, 3, 1)
sage: H3.t_action_on_basis(Permutation([2,1,3]), 1)
T[1, 2, 3]
sage: H3.t_action_on_basis(Permutation([1,3,2]), 2)
T[1, 2, 3]

sage.combinat.symmetric_group_algebra.SymmetricGroupAlgebra(R, n)¶

Returns the symmetric group algebra of order n over R.

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ, 3); QS3
Symmetric group algebra of order 3 over Rational Field
sage: QS3(1)
[1, 2, 3]
sage: QS3(2)
2*[1, 2, 3]
sage: basis = [QS3(p) for p in Permutations(3)]
sage: a = sum(basis); a
[1, 2, 3] + [1, 3, 2] + [2, 1, 3] + [2, 3, 1] + [3, 1, 2] + [3, 2, 1]
sage: a^2
6*[1, 2, 3] + 6*[1, 3, 2] + 6*[2, 1, 3] + 6*[2, 3, 1] + 6*[3, 1, 2] + 6*[3, 2, 1]
sage: a^2 == 6*a
True
sage: b = QS3([3, 1, 2])
sage: b
[3, 1, 2]
sage: b*a
[1, 2, 3] + [1, 3, 2] + [2, 1, 3] + [2, 3, 1] + [3, 1, 2] + [3, 2, 1]
sage: b*a == a
True

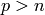The canonical embedding from the symmetric group algebra of order $n$ to the symmetric group algebra of order $p>n$ is available as a coercion:

sage: QS3 = SymmetricGroupAlgebra(QQ, 3)
sage: QS4 = SymmetricGroupAlgebra(QQ, 4)
sage: QS4.coerce_map_from(QS3)
Generic morphism:
  From: Symmetric group algebra of order 3 over Rational Field
  To:   Symmetric group algebra of order 4 over Rational Field

sage: x3  = QS3([3,1,2]) + 2 * QS3([2,3,1]); x3
2*[2, 3, 1] + [3, 1, 2]
sage: QS4(x3)
2*[2, 3, 1, 4] + [3, 1, 2, 4]

This allows for mixed expressions:

sage: x4  = 3*QS4([3, 1, 4, 2])
sage: x3 + x4
2*[2, 3, 1, 4] + [3, 1, 2, 4] + 3*[3, 1, 4, 2]

sage: QS0 = SymmetricGroupAlgebra(QQ, 0)
sage: QS1 = SymmetricGroupAlgebra(QQ, 1)
sage: x0 = QS0([])
sage: x1 = QS1([1])
sage: x0 * x1
[1]
sage: x3 - (2*x0 + x1) - x4
-3*[1, 2, 3, 4] + 2*[2, 3, 1, 4] + [3, 1, 2, 4] - 3*[3, 1, 4, 2]

Caveat: to achieve this, constructing SymmetricGroupAlgebra(QQ, 10) currently triggers the construction of all symmetric group algebras of smaller order. Is this a feature we really want to have?

TESTS:

sage: TestSuite(QS3).run()

class sage.combinat.symmetric_group_algebra.SymmetricGroupAlgebra_n(R, n)¶

Bases: sage.combinat.free_module.CombinatorialFreeModule

canonical_embedding(other)¶

INPUTS:

self, other – two symmetric group algebras with respective order ‘p < n’

Returns the canonical embedding of self into other

EXAMPLES:

sage: QS2 = SymmetricGroupAlgebra(QQ, 2)
sage: QS4 = SymmetricGroupAlgebra(QQ, 4)
sage: phi = QS2.canonical_embedding(QS4); phi
Generic morphism:
  From: Symmetric group algebra of order 2 over Rational Field
  To:   Symmetric group algebra of order 4 over Rational Field

sage: x = QS2([2,1]) + 2 * QS2([1,2])
sage: phi(x)
2*[1, 2, 3, 4] + [2, 1, 3, 4]

sage: loads(dumps(phi))
Generic morphism:
  From: Symmetric group algebra of order 2 over Rational Field
  To:   Symmetric group algebra of order 4 over Rational Field

cpi(p)¶

Returns the centrally primitive idempotent for the symmetric group of order n for the irreducible corresponding indexed by the partition p.

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ,3)
sage: QS3.cpi([2,1])
2/3*[1, 2, 3] - 1/3*[2, 3, 1] - 1/3*[3, 1, 2]
sage: QS3.cpi([3])
1/6*[1, 2, 3] + 1/6*[1, 3, 2] + 1/6*[2, 1, 3] + 1/6*[2, 3, 1] + 1/6*[3, 1, 2] + 1/6*[3, 2, 1]
sage: QS3.cpi([1,1,1])
1/6*[1, 2, 3] - 1/6*[1, 3, 2] - 1/6*[2, 1, 3] + 1/6*[2, 3, 1] + 1/6*[3, 1, 2] - 1/6*[3, 2, 1]

cpis()¶

Returns a list of the centrally primitive idempotents.

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ,3)
sage: a = QS3.cpis()
sage: a[0]  # [3]
1/6*[1, 2, 3] + 1/6*[1, 3, 2] + 1/6*[2, 1, 3] + 1/6*[2, 3, 1] + 1/6*[3, 1, 2] + 1/6*[3, 2, 1]
sage: a[1]  # [2, 1]
2/3*[1, 2, 3] - 1/3*[2, 3, 1] - 1/3*[3, 1, 2]

dft(form='seminormal')¶

Returns the discrete Fourier transform for self.

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ, 3)
sage: QS3.dft()
[   1    1    1    1    1    1]
[   1  1/2   -1 -1/2 -1/2  1/2]
[   0  3/4    0  3/4 -3/4 -3/4]
[   0    1    0   -1    1   -1]
[   1 -1/2    1 -1/2 -1/2 -1/2]
[   1   -1   -1    1    1   -1]

epsilon_ik(itab, ktab, star=0)¶

Returns the seminormal basis element of self corresponding to the pair of tableaux itab and ktab.

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ, 3)
sage: a = QS3.epsilon_ik([[1,2,3]], [[1,2,3]]); a
1/6*[1, 2, 3] + 1/6*[1, 3, 2] + 1/6*[2, 1, 3] + 1/6*[2, 3, 1] + 1/6*[3, 1, 2] + 1/6*[3, 2, 1]
sage: QS3.dft()*vector(a)
(1, 0, 0, 0, 0, 0)
sage: a = QS3.epsilon_ik([[1,2],[3]], [[1,2],[3]]); a
1/3*[1, 2, 3] - 1/6*[1, 3, 2] + 1/3*[2, 1, 3] - 1/6*[2, 3, 1] - 1/6*[3, 1, 2] - 1/6*[3, 2, 1]
sage: QS3.dft()*vector(a)
(0, 0, 0, 0, 1, 0)

jucys_murphy(k)¶

Returns the Jucys-Murphy element J_k for the symmetric group algebra.

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ, 3)
sage: QS3.jucys_murphy(2)
[2, 1, 3]
sage: QS3.jucys_murphy(3)
[1, 3, 2] + [3, 2, 1]

sage: QS4 = SymmetricGroupAlgebra(QQ, 4)
sage: j3 = QS4.jucys_murphy(3); j3
[1, 3, 2, 4] + [3, 2, 1, 4]
sage: j4 = QS4.jucys_murphy(4); j4
[1, 2, 4, 3] + [1, 4, 3, 2] + [4, 2, 3, 1]
sage: j3*j4 == j4*j3
True

sage: QS5 = SymmetricGroupAlgebra(QQ, 5)
sage: QS5.jucys_murphy(4)
[1, 2, 4, 3, 5] + [1, 4, 3, 2, 5] + [4, 2, 3, 1, 5]

monomial_from_smaller_permutation(permutation)¶

Converts the input into a permutation, possibly extending it to the appropriate size, and returns the corresponding basis element.

EXAMPLES:

sage: QS5 = SymmetricGroupAlgebra(QQ, 5)
sage: QS5.monomial_from_smaller_permutation([])
[1, 2, 3, 4, 5]
sage: QS5.monomial_from_smaller_permutation(Permutation([3,1,2]))
[3, 1, 2, 4, 5]
sage: QS5.monomial_from_smaller_permutation([5,3,4,1,2])
[5, 3, 4, 1, 2]

TESTS:

sage: QS5.monomial_from_smaller_permutation([5,3,4,1,2]).parent()
Symmetric group algebra of order 5 over Rational Field

one_basis(*args, **kwds)¶

Returns the identity of the symmetric group, as per AlgebrasWithBasis.ParentMethods.one_basis

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ, 3)
sage: QS3.one_basis()
[1, 2, 3]

product_on_basis(left, right)¶

Returns the product of the basis elements indexed by left and right.

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ, 3)
sage: p1 = Permutation([1,2,3])
sage: p2 = Permutation([2,1,3])
sage: QS3.product_on_basis(p1,p2)
[2, 1, 3]

seminormal_basis()¶

Returns a list of the seminormal basis elements of self.

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ,3)
sage: QS3.seminormal_basis()
[1/6*[1, 2, 3] + 1/6*[1, 3, 2] + 1/6*[2, 1, 3] + 1/6*[2, 3, 1] + 1/6*[3, 1, 2] + 1/6*[3, 2, 1],
1/3*[1, 2, 3] + 1/6*[1, 3, 2] - 1/3*[2, 1, 3] - 1/6*[2, 3, 1] - 1/6*[3, 1, 2] + 1/6*[3, 2, 1],
1/3*[1, 3, 2] + 1/3*[2, 3, 1] - 1/3*[3, 1, 2] - 1/3*[3, 2, 1],
1/4*[1, 3, 2] - 1/4*[2, 3, 1] + 1/4*[3, 1, 2] - 1/4*[3, 2, 1],
1/3*[1, 2, 3] - 1/6*[1, 3, 2] + 1/3*[2, 1, 3] - 1/6*[2, 3, 1] - 1/6*[3, 1, 2] - 1/6*[3, 2, 1],
1/6*[1, 2, 3] - 1/6*[1, 3, 2] - 1/6*[2, 1, 3] + 1/6*[2, 3, 1] + 1/6*[3, 1, 2] - 1/6*[3, 2, 1]]

sage.combinat.symmetric_group_algebra.e(tableau, star=0)¶

The unnormalized Young projection operator.

EXAMPLES:

sage: from sage.combinat.symmetric_group_algebra import e
sage: e([[1,2]])
[1, 2] + [2, 1]
sage: e([[1],[2]])
[1, 2] - [2, 1]

There are differing conventions for the order of the symmetrizers and antisymmetrizers. This example illustrates our conventions:

sage: e([[1,2],[3]])
[1, 2, 3] + [2, 1, 3] - [3, 1, 2] - [3, 2, 1]

sage.combinat.symmetric_group_algebra.e_hat(tab, star=0)¶

The Young projection operator, an idempotent in the rational group algebra.

EXAMPLES:

sage: from sage.combinat.symmetric_group_algebra import e_hat
sage: e_hat([[1,2,3]])
1/6*[1, 2, 3] + 1/6*[1, 3, 2] + 1/6*[2, 1, 3] + 1/6*[2, 3, 1] + 1/6*[3, 1, 2] + 1/6*[3, 2, 1]
sage: e_hat([[1],[2]])
1/2*[1, 2] - 1/2*[2, 1]

There are differing conventions for the order of the symmetrizers and antisymmetrizers. This example illustrates our conventions:

sage: e_hat([[1,2],[3]])
1/3*[1, 2, 3] + 1/3*[2, 1, 3] - 1/3*[3, 1, 2] - 1/3*[3, 2, 1]

sage.combinat.symmetric_group_algebra.e_ik(itab, ktab, star=0)¶

EXAMPLES:

sage: from sage.combinat.symmetric_group_algebra import e_ik
sage: e_ik([[1,2,3]], [[1,2,3]])
[1, 2, 3] + [1, 3, 2] + [2, 1, 3] + [2, 3, 1] + [3, 1, 2] + [3, 2, 1]
sage: e_ik([[1,2,3]], [[1,2,3]], star=1)
[1, 2] + [2, 1]

sage.combinat.symmetric_group_algebra.epsilon(tab, star=0)¶

EXAMPLES:

sage: from sage.combinat.symmetric_group_algebra import epsilon
sage: epsilon([[1,2]])
1/2*[1, 2] + 1/2*[2, 1]
sage: epsilon([[1],[2]])
1/2*[1, 2] - 1/2*[2, 1]

sage.combinat.symmetric_group_algebra.epsilon_ik(itab, ktab, star=0)¶

EXAMPLES:

sage: from sage.combinat.symmetric_group_algebra import epsilon_ik
sage: epsilon_ik([[1,2],[3]], [[1,3],[2]])
1/4*[1, 3, 2] - 1/4*[2, 3, 1] + 1/4*[3, 1, 2] - 1/4*[3, 2, 1]
sage: epsilon_ik([[1,2],[3]], [[1,3],[2]], star=1)
...
ValueError: the two tableaux must be of the same shape

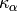sage.combinat.symmetric_group_algebra.kappa(alpha)¶

Returns $\kappa_\alpha$ which is n! divided by the number of standard tableaux of shape $\alpha$ .

EXAMPLES:

sage: from sage.combinat.symmetric_group_algebra import kappa
sage: kappa(Partition([2,1]))
3
sage: kappa([2,1])
3

sage.combinat.symmetric_group_algebra.pi_ik(itab, ktab)¶

EXAMPLES:

sage: from sage.combinat.symmetric_group_algebra import pi_ik
sage: pi_ik([[1,3],[2]], [[1,2],[3]])
[1, 3, 2]

sage.combinat.symmetric_group_algebra.seminormal_test(n)¶

Runs a variety of tests to verify that the construction of the seminormal basis works as desired. The numbers appearing are Theorems in James and Kerber’s ‘Representation Theory of the Symmetric Group’.

EXAMPLES:

sage: from sage.combinat.symmetric_group_algebra import seminormal_test
sage: seminormal_test(3)
True

Symmetric Group Algebra¶

Previous topic

Next topic

This Page

Navigation

Symmetric Group Algebra¶

Previous topic

Next topic

This Page

Quick search

Navigation