Permutations template¶

This file define high level operations on permutations (alphabet, the different rauzy induction, ...) shared by reduced and labeled permutations.

AUTHORS:

Vincent Delecroix (2008-12-20): initial version

TODO:

construct as options different string representations for a permutation
- the two intervals: str
- the two intervals on one line: str_one_line
- the separatrix diagram: str_separatrix_diagram
- twin[0] and twin[1] for reduced permutation
- nothing (useful for Rauzy diagram)

class sage.combinat.iet.template.FlippedPermutation¶

Bases: sage.combinat.iet.template.Permutation

Template for flipped generalized permutations.

Warning

Internal class! Do not use directly!

AUTHORS:

Vincent Delecroix (2008-12-20): initial version

str(sep='n')¶

String representation.

TESTS:

sage: p = iet.GeneralizedPermutation('a a','b b',flips='a')
sage: print p.str()
-a -a
 b  b
 sage: print p.str('/')
 -a -a/ b  b

class sage.combinat.iet.template.FlippedPermutationIET¶

Bases: sage.combinat.iet.template.FlippedPermutation, sage.combinat.iet.template.PermutationIET

Template for flipped Abelian permutations.

Warning

Internal class! Do not use directly!

AUTHORS:

Vincent Delecroix (2008-12-20): initial version

flips()¶

Returns the list of flips.

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a',flips='ac')
sage: p.flips()
['a', 'c']

class sage.combinat.iet.template.FlippedPermutationLI¶

Bases: sage.combinat.iet.template.FlippedPermutation, sage.combinat.iet.template.PermutationLI

Template for flipped quadratic permutations.

Warning

Internal class! Do not use directly!

AUTHORS:

Vincent Delecroix (2008-12-20): initial version

flips()¶

Returns the list of flipped intervals.

EXAMPLES:

sage: p = iet.GeneralizedPermutation('a a','b b',flips='a')
sage: p.flips()
['a']
sage: p = iet.GeneralizedPermutation('a a','b b',flips='b',reduced=True)
sage: p.flips()
['b']

class sage.combinat.iet.template.FlippedRauzyDiagram(p, right_induction=True, left_induction=False, left_right_inversion=False, top_bottom_inversion=False, symmetric=False)¶

Bases: sage.combinat.iet.template.RauzyDiagram

Template for flipped Rauzy diagrams.

AUTHORS:

Vincent Delecroix (2009-09-29): initial version

complete(p, reducible=False)¶

Completion of the Rauzy diagram

Add all successors of p for defined operations in edge_types. Could be used for generating non (strongly) connected Rauzy diagrams. Sometimes, for flipped permutations, the maximal connected graph in all permutations is not strongly connected. Finding such components needs to call most than once the .complete() method.

INPUT:

p - a permutation
reducible - put or not reducible permutations

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a',flips='a')
sage: d = p.rauzy_diagram()
sage: d
Rauzy diagram with 3 permutations
sage: p = iet.Permutation('a b c','c b a',flips='b')
sage: d.complete(p)
sage: d
Rauzy diagram with 8 permutations
sage: p = iet.Permutation('a b c','c b a',flips='a')
sage: d.complete(p)
sage: d
Rauzy diagram with 8 permutations

class sage.combinat.iet.template.Permutation¶

Bases: sage.structure.sage_object.SageObject

Template for all permutations.

Warning

Internal class! Do not use directly!

This class implement generic algorithm (stratum, connected component, ...) and unfies all its children.

alphabet(data=None)¶

Manages the alphabet of self.

If there is no argument, the method returns the alphabet used. If the argument could be converted to an alphabet, this alphabet will be used.

INPUT:

data - None or something that could be converted to an alphabet

OUTPUT:

– either None or the current alphabet

EXAMPLES:

sage: p = iet.Permutation('a b','a b')
sage: p.alphabet([0,1])
sage: p.alphabet() == Alphabet([0,1])
True
sage: p
0 1
0 1
sage: p.alphabet("cd")
sage: p.alphabet() == Alphabet(['c','d'])
True
sage: p
c d
c d

has_rauzy_move(winner='top', side=None)¶

Tests the legality of a Rauzy move.

INPUT:

winner - ‘top’ or ‘bottom’ corresponding to the interval
side - ‘left’ or ‘right’ (defaut)

OUTPUT:

– a boolean

EXAMPLES:

sage: p = iet.Permutation('a b','a b')
sage: p.has_rauzy_move('top','right')
False
sage: p.has_rauzy_move('bottom','right')
False
sage: p.has_rauzy_move('top','left')
False
sage: p.has_rauzy_move('bottom','left')
False

sage: p = iet.Permutation('a b c','b a c')
sage: p.has_rauzy_move('top','right')
False
sage: p.has_rauzy_move('bottom', 'right')
False
sage: p.has_rauzy_move('top','left')
True
sage: p.has_rauzy_move('bottom','left')
True

sage: p = iet.Permutation('a b','b a')
sage: p.has_rauzy_move('top','right')
True
sage: p.has_rauzy_move('bottom','right')
True
sage: p.has_rauzy_move('top','left')
True
sage: p.has_rauzy_move('bottom','left')
True

horizontal_inverse()¶

Returns the top-bottom inverse.

You can use also use the shorter .tb_inverse().

OUTPUT:

– a permutation

EXAMPLES:

sage: p = iet.Permutation('a b','b a')
sage: p.top_bottom_inverse()
b a
a b
sage: p = iet.Permutation('a b','b a',reduced=True)
sage: p.top_bottom_inverse() == p
True

sage: p = iet.Permutation('a b c d','c d a b')
sage: p.top_bottom_inverse()
c d a b
a b c d

TESTS:

sage: p = iet.Permutation('a b','a b')
sage: p == p.top_bottom_inverse()
True
sage: p is p.top_bottom_inverse()
False
sage: p = iet.GeneralizedPermutation('a a','b b',reduced=True)
sage: p == p.top_bottom_inverse()
True
sage: p is p.top_bottom_inverse()
False

left_right_inverse()¶

Returns the left-right inverse.

You can also use the shorter .lr_inverse()

OUTPUT:

– a permutation

EXAMPLES:

sage: p = iet.Permutation('a b c','c a b')
sage: p.left_right_inverse()
c b a
b a c
sage: p = iet.Permutation('a b c d','c d a b')
sage: p.left_right_inverse()
d c b a
b a d c

sage: p = iet.GeneralizedPermutation('a a','b b c c')
sage: p.left_right_inverse()
a a
c c b b

sage: p = iet.Permutation('a b c','c b a',reduced=True)
sage: p.left_right_inverse() == p
True
sage: p = iet.Permutation('a b c','c a b',reduced=True)
sage: q = p.left_right_inverse()
sage: q == p
False
sage: q
a b c
b c a

sage: p = iet.GeneralizedPermutation('a a','b b c c',reduced=True)
sage: p.left_right_inverse() == p
True
sage: p = iet.GeneralizedPermutation('a b b','c c a',reduced=True)
sage: q = p.left_right_inverse()
sage: q == p
False
sage: q
a a b
b c c

TESTS:

sage: p = iet.GeneralizedPermutation('a a','b b')
sage: p.left_right_inverse()
a a
b b
sage: p is p.left_right_inverse()
False
sage: p == p.left_right_inverse()
True

letters()¶

Returns the list of letters of the alphabet used for representation.

The letters used are not necessarily the whole alphabet (for example if the alphabet is infinite).

OUTPUT:

– a list of labels

EXAMPLES:

sage: p = iet.Permutation([1,2],[2,1])
sage: p.alphabet(Alphabet(name="NN"))
sage: p
0 1
1 0
sage: p.letters()
[0, 1]

lr_inverse()¶

Returns the left-right inverse.

You can also use the shorter .lr_inverse()

OUTPUT:

– a permutation

EXAMPLES:

sage: p = iet.Permutation('a b c','c a b')
sage: p.left_right_inverse()
c b a
b a c
sage: p = iet.Permutation('a b c d','c d a b')
sage: p.left_right_inverse()
d c b a
b a d c

sage: p = iet.GeneralizedPermutation('a a','b b c c')
sage: p.left_right_inverse()
a a
c c b b

sage: p = iet.Permutation('a b c','c b a',reduced=True)
sage: p.left_right_inverse() == p
True
sage: p = iet.Permutation('a b c','c a b',reduced=True)
sage: q = p.left_right_inverse()
sage: q == p
False
sage: q
a b c
b c a

sage: p = iet.GeneralizedPermutation('a a','b b c c',reduced=True)
sage: p.left_right_inverse() == p
True
sage: p = iet.GeneralizedPermutation('a b b','c c a',reduced=True)
sage: q = p.left_right_inverse()
sage: q == p
False
sage: q
a a b
b c c

TESTS:

sage: p = iet.GeneralizedPermutation('a a','b b')
sage: p.left_right_inverse()
a a
b b
sage: p is p.left_right_inverse()
False
sage: p == p.left_right_inverse()
True

rauzy_move(winner, side='right', iteration=1)¶

Returns the permutation after a Rauzy move.

INPUT:

winner - ‘top’ or ‘bottom’ interval
side - ‘right’ or ‘left’ (defaut: ‘right’) corresponding to the side on which the Rauzy move must be performed.
iteration - a non negative integer

OUTPUT:

a permutation

TESTS:

sage: p = iet.Permutation('a b','b a')
sage: p.rauzy_move(winner=0, side='right') == p
True
sage: p.rauzy_move(winner=1, side='right') == p
True
sage: p.rauzy_move(winner=0, side='left') == p
True
sage: p.rauzy_move(winner=1, side='left') == p
True

sage: p = iet.Permutation('a b c','c b a')
sage: p.rauzy_move(winner=0, side='right')
a b c
c a b
sage: p.rauzy_move(winner=1, side='right')
a c b
c b a
sage: p.rauzy_move(winner=0, side='left')
a b c
b c a
sage: p.rauzy_move(winner=1, side='left')
b a c
c b a

str(sep='n')¶

A string representation of the generalized permutation.

INPUT:

sep - (default: ‘n’) a separator for the two intervals

OUTPUT:

string – the string that represents the permutation

EXAMPLES:

For permutations of iet:

sage: p = iet.Permutation('a b c','c b a')
sage: p.str()
'a b c\nc b a'
sage: p.str(sep=' | ')
'a b c | c b a'

..the permutation can be rebuilt from the standard string:

sage: p == iet.Permutation(p.str())
True

For permutations of li:

sage: p = iet.GeneralizedPermutation('a b b','c c a')
sage: p.str()
'a b b\nc c a'
sage: p.str(sep=' | ')
'a b b | c c a'

..the generalized permutation can be rebuilt from the standard string:

sage: p == iet.GeneralizedPermutation(p.str())
True

symmetric()¶

Returns the symmetric permutation.

The symmetric permutation is the composition of the top-bottom inversion and the left-right inversion (which are geometrically orientation reversing).

OUTPUT:

– a permutation

EXAMPLES:

sage: p = iet.Permutation("a b c","c b a")
sage: p.symmetric()
a b c
c b a
sage: q = iet.Permutation("a b c d","b d a c")
sage: q.symmetric()
c a d b
d c b a

sage: p = iet.Permutation('a b c d','c a d b')
sage: q = p.symmetric()
sage: q1 = p.tb_inverse().lr_inverse()
sage: q2 = p.lr_inverse().tb_inverse()
sage: q == q1
True
sage: q == q2
True

TESTS:

sage: p = iet.GeneralizedPermutation('a a b','b c c',reduced=True)
sage: q = p.symmetric()
sage: q1 = p.tb_inverse().lr_inverse()
sage: q2 = p.lr_inverse().tb_inverse()
sage: q == q1
True
sage: q == q2
True

sage: p = iet.GeneralizedPermutation('a a b','b c c',reduced=True,flips='a')
sage: q = p.symmetric()
sage: q1 = p.tb_inverse().lr_inverse()
sage: q2 = p.lr_inverse().tb_inverse()
sage: q == q1
True
sage: q == q2
True

tb_inverse()¶

Returns the top-bottom inverse.

You can use also use the shorter .tb_inverse().

OUTPUT:

– a permutation

EXAMPLES:

sage: p = iet.Permutation('a b','b a')
sage: p.top_bottom_inverse()
b a
a b
sage: p = iet.Permutation('a b','b a',reduced=True)
sage: p.top_bottom_inverse() == p
True

sage: p = iet.Permutation('a b c d','c d a b')
sage: p.top_bottom_inverse()
c d a b
a b c d

TESTS:

sage: p = iet.Permutation('a b','a b')
sage: p == p.top_bottom_inverse()
True
sage: p is p.top_bottom_inverse()
False
sage: p = iet.GeneralizedPermutation('a a','b b',reduced=True)
sage: p == p.top_bottom_inverse()
True
sage: p is p.top_bottom_inverse()
False

top_bottom_inverse()¶

Returns the top-bottom inverse.

You can use also use the shorter .tb_inverse().

OUTPUT:

– a permutation

EXAMPLES:

sage: p = iet.Permutation('a b','b a')
sage: p.top_bottom_inverse()
b a
a b
sage: p = iet.Permutation('a b','b a',reduced=True)
sage: p.top_bottom_inverse() == p
True

sage: p = iet.Permutation('a b c d','c d a b')
sage: p.top_bottom_inverse()
c d a b
a b c d

TESTS:

sage: p = iet.Permutation('a b','a b')
sage: p == p.top_bottom_inverse()
True
sage: p is p.top_bottom_inverse()
False
sage: p = iet.GeneralizedPermutation('a a','b b',reduced=True)
sage: p == p.top_bottom_inverse()
True
sage: p is p.top_bottom_inverse()
False

vertical_inverse()¶

Returns the left-right inverse.

You can also use the shorter .lr_inverse()

OUTPUT:

– a permutation

EXAMPLES:

sage: p = iet.Permutation('a b c','c a b')
sage: p.left_right_inverse()
c b a
b a c
sage: p = iet.Permutation('a b c d','c d a b')
sage: p.left_right_inverse()
d c b a
b a d c

sage: p = iet.GeneralizedPermutation('a a','b b c c')
sage: p.left_right_inverse()
a a
c c b b

sage: p = iet.Permutation('a b c','c b a',reduced=True)
sage: p.left_right_inverse() == p
True
sage: p = iet.Permutation('a b c','c a b',reduced=True)
sage: q = p.left_right_inverse()
sage: q == p
False
sage: q
a b c
b c a

sage: p = iet.GeneralizedPermutation('a a','b b c c',reduced=True)
sage: p.left_right_inverse() == p
True
sage: p = iet.GeneralizedPermutation('a b b','c c a',reduced=True)
sage: q = p.left_right_inverse()
sage: q == p
False
sage: q
a a b
b c c

TESTS:

sage: p = iet.GeneralizedPermutation('a a','b b')
sage: p.left_right_inverse()
a a
b b
sage: p is p.left_right_inverse()
False
sage: p == p.left_right_inverse()
True

class sage.combinat.iet.template.PermutationIET¶

Bases: sage.combinat.iet.template.Permutation

Template for permutation from Interval Exchange Transformation.

Warning

Internal class! Do not use directly!

AUTHOR:

Vincent Delecroix (2008-12-20): initial version

arf_invariant()¶

Returns the Arf invariant of the suspension of self.

OUTPUT:

integer – 0 or 1

EXAMPLES:

Permutations from the odd and even component of H(2,2,2):

sage: a = range(10)
sage: b1 = [3,2,4,6,5,7,9,8,1,0]
sage: b0 = [6,5,4,3,2,7,9,8,1,0]
sage: p1 = iet.Permutation(a,b1)
sage: print p1.arf_invariant()
1
sage: p0 = iet.Permutation(a,b0)
sage: print p0.arf_invariant()
0

Permutations from the odd and even component of H(4,4):

sage: a = range(11)
sage: b1 = [3,2,5,4,6,8,7,10,9,1,0]
sage: b0 = [5,4,3,2,6,8,7,10,9,1,0]
sage: p1 = iet.Permutation(a,b1)
sage: print p1.arf_invariant()
1
sage: p0 = iet.Permutation(a,b0)
sage: print p0.arf_invariant()
0

REFERENCES:

[Jo80] D. Johnson, “Spin structures and quadratic forms on surfaces”, J. London Math. Soc (2), 22, 1980, 365-373

[KoZo03] M. Kontsevich, A. Zorich “Connected components of the moduli spaces of Abelian differentials with prescribed singularities”, Inventiones Mathematicae, 153, 2003, 631-678

attached_in_degree()¶

Returns the degree of the singularity at the right of the interval.

OUTPUT:

– a positive integer

EXAMPLES:

sage: p1 = iet.Permutation('a b c d e f g','d c g f e b a')
sage: p2 = iet.Permutation('a b c d e f g','e d c g f b a')
sage: p1.attached_in_degree()
1
sage: p2.attached_in_degree()
3

attached_out_degree()¶

Returns the degree of the singularity at the left of the interval.

OUTPUT:

– a positive integer

EXAMPLES:

sage: p1 = iet.Permutation('a b c d e f g','d c g f e b a')
sage: p2 = iet.Permutation('a b c d e f g','e d c g f b a')
sage: p1.attached_out_degree()
3
sage: p2.attached_out_degree()
1

attached_type()¶

Return the singularity degree attached on the left and the right.

OUTPUT:

([degre], angle_parity) – if the same singularity is attached on the left and right

([left_degree, right_degree], 0) – the degrees at the left and the right which are different singularitites

EXAMPLES:

With two intervals:

sage: p = iet.Permutation('a b','b a')
sage: p.attached_type()
([0], 1)

With three intervals:

sage: p = iet.Permutation('a b c','b c a')
sage: p.attached_type()
([0], 1)

sage: p = iet.Permutation('a b c','c a b')
sage: p.attached_type()
([0], 1)

sage: p = iet.Permutation('a b c','c b a')
sage: p.attached_type()
([0, 0], 0)

With four intervals:

sage: p = iet.Permutation('1 2 3 4','4 3 2 1')
sage: p.attached_type()
([2], 0)

connected_component(marked_separatrix='no')¶

Returns a connected components of a stratum.

EXAMPLES:

Permutations from the stratum H(6):

sage: a = range(8)
sage: b_hyp = [7,6,5,4,3,2,1,0]
sage: b_odd = [3,2,5,4,7,6,1,0]
sage: b_even = [5,4,3,2,7,6,1,0]
sage: p_hyp = iet.Permutation(a, b_hyp)
sage: p_odd = iet.Permutation(a, b_odd)
sage: p_even = iet.Permutation(a, b_even)
sage: print p_hyp.connected_component()
H_hyp(6)
sage: print p_odd.connected_component()
H_odd(6)
sage: print p_even.connected_component()
H_even(6)

Permutations from the stratum H(4,4):

sage: a = range(11)
sage: b_hyp = [10,9,8,7,6,5,4,3,2,1,0]
sage: b_odd = [3,2,5,4,6,8,7,10,9,1,0]
sage: b_even = [5,4,3,2,6,8,7,10,9,1,0]
sage: p_hyp = iet.Permutation(a,b_hyp)
sage: p_odd = iet.Permutation(a,b_odd)
sage: p_even = iet.Permutation(a,b_even)
sage: p_hyp.stratum() == AbelianStratum(4,4)
True
sage: print p_hyp.connected_component()
H_hyp(4, 4)
sage: p_odd.stratum() == AbelianStratum(4,4)
True
sage: print p_odd.connected_component()
H_odd(4, 4)
sage: p_even.stratum() == AbelianStratum(4,4)
True
sage: print p_even.connected_component()
H_even(4, 4)

As for stratum you can specify that you want to attach the singularity on the left of the interval using the option marked_separatrix:

sage: a = [1,2,3,4,5,6,7,8,9]
sage: b4_odd = [4,3,6,5,7,9,8,2,1]
sage: b4_even = [6,5,4,3,7,9,8,2,1]
sage: b2_odd = [4,3,5,7,6,9,8,2,1]
sage: b2_even = [7,6,5,4,3,9,8,2,1]
sage: p4_odd = iet.Permutation(a,b4_odd)
sage: p4_even = iet.Permutation(a,b4_even)
sage: p2_odd = iet.Permutation(a,b2_odd)
sage: p2_even = iet.Permutation(a,b2_even)
sage: p4_odd.connected_component(marked_separatrix='out')
H_odd^out(4, 2)
sage: p4_even.connected_component(marked_separatrix='out')
H_even^out(4, 2)
sage: p2_odd.connected_component(marked_separatrix='out')
H_odd^out(2, 4)
sage: p2_even.connected_component(marked_separatrix='out')
H_even^out(2, 4)
sage: p2_odd.connected_component() == p4_odd.connected_component()
True
sage: p2_odd.connected_component('out') == p4_odd.connected_component('out')
False

cylindric()¶

Returns a permutation in the Rauzy class such that

twin[0][-1] == 0 twin[1][-1] == 0

TESTS:

sage: p = iet.Permutation('a b c','c b a')
sage: p.cylindric() == p
True
sage: p = iet.Permutation('a b c d','b d a c')
sage: q = p.cylindric()
sage: q[0][0] == q[1][-1]
True
sage: q[1][0] == q[1][0]
True

decompose()¶

Returns the decomposition of self.

OUTPUT:

– a list of permutations

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a').decompose()[0]
sage: p
a b c
c b a

sage: p1,p2,p3 = iet.Permutation('a b c d e','b a c e d').decompose()
sage: p1
a b
b a
sage: p2
c
c
sage: p3
d e
e d

erase_marked_points()¶

Returns a permutation equivalent to self but without marked points.

EXAMPLES:

sage: a = iet.Permutation('a b1 b2 c d', 'd c b1 b2 a')
sage: a.erase_marked_points()
a b1 c d
d c b1 a

genus()¶

Returns the genus corresponding to any suspension of the permutation.

OUTPUT:

– a positive integer

EXAMPLES:

sage: p = iet.Permutation('a b c', 'c b a')
sage: p.genus()
1

sage: p = iet.Permutation('a b c d','d c b a')
sage: p.genus()
2

REFERENCES:: Veech

intersection_matrix()¶

Returns the intersection matrix.

This 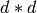$d*d$ antisymmetric matrix is given by the rule :

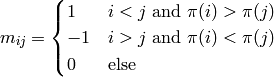
$m_{ij} = \begin{cases} 1 & \text{$i < j$ and $\pi(i) > \pi(j)$} \\ -1 & \text{$i > j$ and $\pi(i) < \pi(j)$} \\ 0 & \text{else} \end{cases}$

OUTPUT:

a matrix

EXAMPLES:

sage: p = iet.Permutation('a b c d','d c b a')
sage: p.intersection_matrix()
[ 0  1  1  1]
[-1  0  1  1]
[-1 -1  0  1]
[-1 -1 -1  0]

sage: p = iet.Permutation('1 2 3 4 5','5 3 2 4 1')
sage: p.intersection_matrix()
[ 0  1  1  1  1]
[-1  0  1  0  1]
[-1 -1  0  0  1]
[-1  0  0  0  1]
[-1 -1 -1 -1  0]

is_cylindric()¶

Returns True if the permutation is Rauzy_1n.

A permutation is cylindric if 1 and n are exchanged.

EXAMPLES:

sage: iet.Permutation('1 2 3','3 2 1').is_cylindric()
True
sage: iet.Permutation('1 2 3','2 1 3').is_cylindric()
False

is_hyperelliptic()¶

Returns True if the permutation is in the class of the symmetric permutations (with eventual marked points).

This is equivalent to say that the suspension lives in an hyperelliptic stratum of Abelian differentials H_hyp(2g-2) or H_hyp(g-1, g-1) with some marked points.

EXAMPLES:

sage: iet.Permutation('a b c d','d c b a').is_hyperelliptic()
True
sage: iet.Permutation('0 1 2 3 4 5','5 2 1 4 3 0').is_hyperelliptic()
False

REFERENCES:

Gerard Rauzy, “Echanges d’intervalles et transformations induites”, Acta Arith. 34, no. 3, 203-212, 1980

M. Kontsevich, A. Zorich “Connected components of the moduli space of Abelian differentials with prescripebd singularities” Invent. math. 153, 631-678 (2003)

is_irreducible(return_decomposition=False)¶

Tests the irreducibility.

An abelian permutation p = (p0,p1) is reducible if: set(p0[:i]) = set(p1[:i]) for an i < len(p0)

OUTPUT:

a boolean

EXAMPLES:

sage: p = iet.Permutation('a b c', 'c b a')
sage: p.is_irreducible()
True

sage: p = iet.Permutation('a b c', 'b a c')
sage: p.is_irreducible()
False

order_of_rauzy_action(winner, side=None)¶

Returns the order of the action of a Rauzy move.

INPUT:

winner - string 'top' or 'bottom'
side - string 'left' or 'right'

OUTPUT:

An integer corresponding to the order of the Rauzy action.

EXAMPLES:

sage: p = iet.Permutation('a b c d','d a c b')
sage: p.order_of_rauzy_action('top', 'right')
3
sage: p.order_of_rauzy_action('bottom', 'right')
2
sage: p.order_of_rauzy_action('top', 'left')
1
sage: p.order_of_rauzy_action('bottom', 'left')
3

separatrix_diagram(side=False)¶

Returns the separatrix diagram of the permutation.

INPUT:

side - boolean

OUTPUT:

– a list of lists

EXAMPLES:

sage: iet.Permutation([0, 1], [1, 0]).separatrix_diagram()
[[(1, 0), (1, 0)]]

sage: iet.Permutation('a b c d','d c b a').separatrix_diagram()
[[('d', 'a'), 'b', 'c', ('d', 'a'), 'b', 'c']]

stratum(marked_separatrix='no')¶

Returns the strata in which any suspension of this permutation lives.

OUTPUT:

a stratum of Abelian differentials

EXAMPLES:

sage: p = iet.Permutation('a b c', 'c b a')
sage: print p.stratum()
H(0, 0)

sage: p = iet.Permutation('a b c d', 'd a b c')
sage: print p.stratum()
H(0, 0, 0)

sage: p = iet.Permutation(range(9), [8,5,2,7,4,1,6,3,0])
sage: print p.stratum()
H(1, 1, 1, 1)

You can specify that you want to attach the singularity on the left (or on the right) with the option marked_separatrix:

sage: a = 'a b c d e f g h i j'
sage: b3 = 'd c g f e j i h b a'
sage: b2 = 'd c e g f j i h b a'
sage: b1 = 'e d c g f h j i b a'
sage: p3 = iet.Permutation(a, b3)
sage: p3.stratum()
H(3, 2, 1)
sage: p3.stratum(marked_separatrix='out')
H^out(3, 2, 1)
sage: p2 = iet.Permutation(a, b2)
sage: p2.stratum()
H(3, 2, 1)
sage: p2.stratum(marked_separatrix='out')
H^out(2, 3, 1)
sage: p1 = iet.Permutation(a, b1)
sage: p1.stratum()
H(3, 2, 1)
sage: p1.stratum(marked_separatrix='out')
H^out(1, 3, 2)

AUTHORS:

Vincent Delecroix (2008-12-20)

to_permutation()¶

Returns the permutation as an element of the symetric group.

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a')
sage: p.to_permutation()
[3, 2, 1]

sage: p = Permutation([2,4,1,3])
sage: q = iet.Permutation(p)
sage: q.to_permutation() == p
True

class sage.combinat.iet.template.PermutationLI¶

Bases: sage.combinat.iet.template.Permutation

Template for quadratic permutation.

Warning

Internal class! Do not use directly!

AUTHOR:

Vincent Delecroix (2008-12-20): initial version

has_right_rauzy_move(winner)¶

Test of Rauzy movability (with an eventual specified choice of winner)

A quadratic (or generalized) permutation is rauzy_movable type depending on the possible length of the last interval. It’s dependent of the length equation.

INPUT:

winner - the integer ‘top’ or ‘bottom’

EXAMPLES:

sage: p = iet.GeneralizedPermutation('a a','b b')
sage: p.has_right_rauzy_move('top')
False
sage: p.has_right_rauzy_move('bottom')
False

sage: p = iet.GeneralizedPermutation('a a b','b c c')
sage: p.has_right_rauzy_move('top')
True
sage: p.has_right_rauzy_move('bottom')
True

sage: p = iet.GeneralizedPermutation('a a','b b c c')
sage: p.has_right_rauzy_move('top')
True
sage: p.has_right_rauzy_move('bottom')
False

sage: p = iet.GeneralizedPermutation('a a b b','c c')
sage: p.has_right_rauzy_move('top')
False
sage: p.has_right_rauzy_move('bottom')
True

is_irreducible(return_decomposition=False)¶

Test of reducibility

A quadratic (or generalized) permutation is reducible if there exist a decomposition

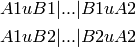
$A1 u B1 | ... | B1 u A2 A1 u B2 | ... | B2 u A2$

where no corners is empty, or exactly one corner is empty and it is on the left, or two and they are both on the right or on the left.

INPUT:

you can eventually set return_decomposition to True

OUTPUT:

An integer, or an integer and a tuple.

if return_decomposition is True, returns a 2-uple (test,decomposition) where test is the preceding test and decomposition is a 4-uple (A11,A12,A21,A22) where:

A11 = A1 u BA A12 = B1 u A2 A21 = A1 u B2 A22 = B2 u A2

REFERENCES:

Boissy-Lanneau

EXAMPLES:

sage: iet.GeneralizedPermutation('a a','b b').is_irreducible()
False
sage: iet.GeneralizedPermutation('a a b','b c c').is_irreducible()
True

AUTHORS:

Vincent Delecroix (2008-12-20)

class sage.combinat.iet.template.RauzyDiagram(p, right_induction=True, left_induction=False, left_right_inversion=False, top_bottom_inversion=False, symmetric=False)¶

Bases: sage.structure.sage_object.SageObject

Template for Rauzy diagrams.

AUTHORS:

Vincent Delecroix (2008-12-20): initial version

class Path(parent, *data)¶

Bases: sage.structure.sage_object.SageObject

Path in Rauzy diagram.

A path in a Rauzy diagram corresponds to a subsimplex of the simplex of lengths. This correspondance is obtained via the Rauzy induction. To a idoc IET we can associate a unique path in a Rauzy diagram. This establishes a correspondance between infinite full path in Rauzy diagram and equivalence topologic class of IET.

append(edge_type)¶

Append an edge to the path.

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram()
sage: g = r.path(p)
sage: g.append('top')
sage: g
Path of length 1 in a Rauzy diagram
sage: g.append('bottom')
sage: g
Path of length 2 in a Rauzy diagram

composition(function, composition=None)¶

Compose an edges function on a path

INPUT:

path - either a Path or a tuple describing a path
function - function must be of the form
composition - the composition function

AUTHOR:

Vincent Delecroix (2009-09-29)

EXAMPLES:

sage: p = iet.Permutation('a b','b a')
sage: r = p.rauzy_diagram()
sage: def f(i,t):
...       if t is None: return []
...       return [t]
sage: g = r.path(p)
sage: g.composition(f,list.__add__)
[]
sage: g = r.path(p,0,1)
sage: g.composition(f, list.__add__)
[0, 1]

edge_types()¶

Returns the edge types of the path.

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram()
sage: g = r.path(p, 0, 1)
sage: g.edge_types()
[0, 1]

end()¶

Returns the last vertex of the path.

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram()
sage: g1 = r.path(p, 't', 'b', 't')
sage: g1.end() == p
True
sage: g2 = r.path(p, 'b', 't', 'b')
sage: g2.end() == p
True

extend(path)¶

Extends self with another path.

EXAMPLES:

sage: p = iet.Permutation('a b c d','d c b a')
sage: r = p.rauzy_diagram()
sage: g1 = r.path(p,'t','t')
sage: g2 = r.path(p.rauzy_move('t',iteration=2),'b','b')
sage: g = r.path(p,'t','t','b','b')
sage: g == g1 + g2
True
sage: g = copy(g1)
sage: g.extend(g2)
sage: g == g1 + g2
True

is_loop()¶

Tests whether the path is a loop (start point = end point).

EXAMPLES:

sage: p = iet.Permutation('a b','b a')
sage: r = p.rauzy_diagram()
sage: r.path(p).is_loop()
True
sage: r.path(p,0,1,0,0).is_loop()
True

losers()¶

Returns a list of the loosers on the path.

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram()
sage: g0 = r.path(p,'t','b','t')
sage: g0.losers()
['a', 'c', 'b']
sage: g1 = r.path(p,'b','t','b')
sage: g1.losers()
['c', 'a', 'b']

pop()¶

Pops the queue of the path

OUTPUT:

a path corresponding to the last edge

EXAMPLES:

sage: p = iet.Permutation('a b','b a')
sage: r = p.rauzy_diagram()
sage: g = r.path(p,0,1,0)
sage: g0,g1,g2,g3 = g[0], g[1], g[2], g[3]
sage: g.pop() == r.path(g2,0)
True
sage: g == r.path(g0,0,1)
True
sage: g.pop() == r.path(g1,1)
True
sage: g == r.path(g0,0)
True
sage: g.pop() == r.path(g0,0)
True
sage: g == r.path(g0)
True
sage: g.pop() == r.path(g0)
True

right_composition(function, composition=None)¶

Compose an edges function on a path

INPUT:

function - function must be of the form (indice,type) -> element. Moreover function(None,None) must be an identity element for initialization.
composition - the composition function for the function. * if None (defaut None)

TEST:

sage: p = iet.Permutation('a b','b a')
sage: r = p.rauzy_diagram()
sage: def f(i,t):
...       if t is None: return []
...       return [t]
sage: g = r.path(p)
sage: g.right_composition(f,list.__add__)
[]
sage: g = r.path(p,0,1)
sage: g.right_composition(f, list.__add__)
[1, 0]

start()¶

Returns the first vertex of the path.

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram()
sage: g = r.path(p, 't', 'b')
sage: g.start() == p
True

winners()¶

Returns the winner list associated to the edge of the path.

EXAMPLES:

sage: p = iet.Permutation('a b','b a')
sage: r = p.rauzy_diagram()
sage: r.path(p).winners()
[]
sage: r.path(p,0).winners()
['b']
sage: r.path(p,1).winners()
['a']

RauzyDiagram.alphabet(data=None)¶

TESTS:

sage: r = iet.RauzyDiagram('a b','b a')
sage: r.alphabet() == Alphabet(['a','b'])
True
sage: r = iet.RauzyDiagram([0,1],[1,0])
sage: r.alphabet() == Alphabet([0,1])
True

RauzyDiagram.cardinality()¶

Returns the number of permutations in this Rauzy diagram.

OUTPUT:

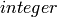$integer$ - the number of vertices in the diagram

EXAMPLES:

sage: r = iet.RauzyDiagram('a b','b a')
sage: r.cardinality()
1
sage: r = iet.RauzyDiagram('a b c','c b a')
sage: r.cardinality()
3
sage: r = iet.RauzyDiagram('a b c d','d c b a')
sage: r.cardinality()
7

RauzyDiagram.complete(p)¶

Completion of the Rauzy diagram.

Add to the Rauzy diagram all permutations that are obtained by successive operations defined by edge_types(). The permutation must be of the same type and the same length as the one used for the creation.

INPUT:

p - a permutation of Interval exchange transformation

Rauzy diagram is the reunion of all permutations that could be obtained with successive rauzy moves. This function just use the functions __getitem__ and has_rauzy_move and rauzy_move which must be defined for child and their corresponding permutation types.

TEST:

sage: r = iet.RauzyDiagram('a b c','c b a')   #indirect doctest
sage: r = iet.RauzyDiagram('a b c','c b a',left_induction=True) #indirect doctest
sage: r = iet.RauzyDiagram('a b c','c b a',symmetric=True)   #indirect doctest
sage: r = iet.RauzyDiagram('a b c','c b a',lr_inversion=True)   #indirect doctest
sage: r = iet.RauzyDiagram('a b c','c b a',tb_inversion=True)   #indirect doctest

RauzyDiagram.edge_iterator()¶

Returns an iterator over the edges of the graph.

EXAMPLES:

sage: p = iet.Permutation('a b','b a')
sage: r = p.rauzy_diagram()
sage: for e in r.edge_iterator(): 
...    print e[0].str(sep='/'), '-->', e[1].str(sep='/')
a b/b a --> a b/b a
a b/b a --> a b/b a

RauzyDiagram.edge_to_loser(p=None, edge_type=None)¶

Return the corresponding loser

TEST:

sage: r = iet.RauzyDiagram('a b','b a')
sage: r.edge_to_loser(None,None)
[]

RauzyDiagram.edge_to_matrix(p=None, edge_type=None)¶

Return the corresponding matrix

INPUT:

p - a permutation
edge_type - 0 or 1 corresponding to the type of the edge

OUTPUT:

A matrix

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a')
sage: d = p.rauzy_diagram()
sage: print d.edge_to_matrix(p,1)
[1 0 1]
[0 1 0]
[0 0 1]

RauzyDiagram.edge_to_winner(p=None, edge_type=None)¶

Return the corresponding winner

TEST:

sage: r = iet.RauzyDiagram('a b','b a')
sage: r.edge_to_winner(None,None)
[]

RauzyDiagram.edge_types()¶

Print information about edges.

EXAMPLES:

sage: r = iet.RauzyDiagram('a b', 'b a')
sage: r.edge_types()
0: rauzy_move(0, -1) 
1: rauzy_move(1, -1)

sage: r = iet.RauzyDiagram('a b', 'b a', left_induction=True)
sage: r.edge_types()
0: rauzy_move(0, -1)
1: rauzy_move(1, -1)
2: rauzy_move(0, 0)
3: rauzy_move(1, 0)

sage: r = iet.RauzyDiagram('a b',' b a',symmetric=True)
sage: r.edge_types()
0: rauzy_move(0, -1)
1: rauzy_move(1, -1)
2: symmetric()

RauzyDiagram.edge_types_index(data)¶

Try to convert the data as an edge type.

INPUT:

data - a string

OUTPUT:

integer

EXAMPLES:

For a standard Rauzy diagram (only right induction) the 0 index corresponds to the ‘top’ induction and the index 1 corresponds to the ‘bottom’ one:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram()
sage: r.edge_types_index('top')
0
sage: r[p][0] == p.rauzy_move('top')
True
sage: r.edge_types_index('bottom')
1
sage: r[p][1] == p.rauzy_move('bottom')
True

The special operations (inversion and symmetry) always appears after the different Rauzy inductions:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram(symmetric=True)
sage: r.edge_types_index('symmetric')
2
sage: r[p][2] == p.symmetric()
True

This function always try to resolve conflictuous name. If it’s impossible a ValueError is raised:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram(left_induction=True)
sage: r.edge_types_index('top')
...
ValueError: left and right inductions must be differentiated
sage: r.edge_types_index('top_right')
0
sage: r[p][0] == p.rauzy_move(0)
True
sage: r.edge_types_index('bottom_left')
3
sage: r[p][3] == p.rauzy_move('bottom', 'left')
True

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram(left_right_inversion=True,top_bottom_inversion=True)
sage: r.edge_types_index('inversion')
...
ValueError: left-right and top-bottom inversions must be differentiated
sage: r.edge_types_index('lr_inverse')
2 
sage: p.lr_inverse() == r[p][2]
True
sage: r.edge_types_index('tb_inverse')
3
sage: p.tb_inverse() == r[p][3]
True

Short names are accepted:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram(right_induction='top',top_bottom_inversion=True)
sage: r.edge_types_index('top_rauzy_move')
0
sage: r.edge_types_index('t')
0
sage: r.edge_types_index('tb')
1
sage: r.edge_types_index('inversion')
1
sage: r.edge_types_index('inverse')
1
sage: r.edge_types_index('i')
1

RauzyDiagram.edges(labels=True)¶

Returns a list of the edges.

EXAMPLES:

sage: r = iet.RauzyDiagram('a b','b a')
sage: len(r.edges())
2

RauzyDiagram.graph()¶

Returns the Rauzy diagram as a Graph object

The graph returned is more precisely a DiGraph (directed graph) with loops and multiedges allowed.

EXAMPLES:

sage: r = iet.RauzyDiagram('a b c','c b a')
sage: r
Rauzy diagram with 3 permutations
sage: r.graph()
Looped multi-digraph on 3 vertices

RauzyDiagram.letters()¶

Returns the letters used by the RauzyDiagram.

EXAMPLES:

sage: r = iet.RauzyDiagram('a b','b a')
sage: r.alphabet()
Ordered Alphabet ['a', 'b']
sage: r.letters()
['a', 'b']
sage: r.alphabet('ABCDEF')
sage: r.alphabet()
Ordered Alphabet ['A', 'B', 'C', 'D', 'E', 'F']
sage: r.letters()
['A', 'B']

RauzyDiagram.path(*data)¶

Returns a path over this Rauzy diagram.

INPUT:

initial_vertex - the initial vertex (starting point of the path)
data - a sequence of edges

EXAMPLES:

sage: p = iet.Permutation('a b c','c b a')
sage: r = p.rauzy_diagram()
sage: g = r.path(p, 'top', 'bottom')

RauzyDiagram.vertex_iterator()¶

Returns an iterator over the vertices

EXAMPLES:

sage: r = iet.RauzyDiagram('a b','b a')
sage: for p in r.vertex_iterator(): print p
a b
b a

sage: r = iet.RauzyDiagram('a b c d','d c b a')
sage: from itertools import ifilter
sage: r_1n = ifilter(lambda x: x.is_cylindric(), r)
sage: for p in r_1n: print p
a b c d
d c b a

RauzyDiagram.vertices()¶

Returns a list of the vertices.

EXAMPLES:

sage: r = iet.RauzyDiagram('a b','b a')
sage: for p in r.vertices(): print p
a b
b a

sage.combinat.iet.template.interval_conversion(interval=None)¶

Converts the argument in 0 or 1.

INPUT:

winner - ‘top’ (or ‘t’ or 0) or bottom (or ‘b’ or 1)

OUTPUT:

integer – 0 or 1

TESTS:

sage: from sage.combinat.iet.template import interval_conversion
sage: interval_conversion('top')
0
sage: interval_conversion('t')
0
sage: interval_conversion(0)
0
sage: interval_conversion('bottom')
1
sage: interval_conversion('b')
1
sage: interval_conversion(1)
1

sage.combinat.iet.template.labelize_flip(couple)¶

Returns a string from a 2-uple couple of the form (name, flip).

TESTS:

sage: from sage.combinat.iet.template import labelize_flip
sage: labelize_flip((0,1))
' 0'
sage: labelize_flip((0,-1))
'-0'

sage.combinat.iet.template.side_conversion(side=None)¶

Converts the argument in 0 or -1.

INPUT:

side - either ‘left’ (or ‘l’ or 0) or ‘right’ (or ‘r’ or -1)

OUTPUT:

integer – 0 or -1

TESTS:

sage: from sage.combinat.iet.template import side_conversion
sage: side_conversion('left')
0
sage: side_conversion('l')
0
sage: side_conversion(0)
0
sage: side_conversion('right')
-1
sage: side_conversion('r')
-1
sage: side_conversion(1)
-1
sage: side_conversion(-1)
-1

sage.combinat.iet.template.twin_list_iet(a=None)¶

Returns the twin list of intervals.

The twin intervals is the correspondance between positions of labels in such way that a[interval][position] is a[1-interval][twin[interval][position]]

INPUT:

a - two lists of labels

OUTPUT:

list – a list of two lists of integers

TESTS:

sage: from sage.combinat.iet.template import twin_list_iet
sage: twin_list_iet([['a','b','c'],['a','b','c']])
[[0, 1, 2], [0, 1, 2]]
sage: twin_list_iet([['a','b','c'],['a','c','b']])
[[0, 2, 1], [0, 2, 1]]
sage: twin_list_iet([['a','b','c'],['b','a','c']])
[[1, 0, 2], [1, 0, 2]]
sage: twin_list_iet([['a','b','c'],['b','c','a']])
[[2, 0, 1], [1, 2, 0]]
sage: twin_list_iet([['a','b','c'],['c','a','b']])
[[1, 2, 0], [2, 0, 1]]
sage: twin_list_iet([['a','b','c'],['c','b','a']])
[[2, 1, 0], [2, 1, 0]]

sage.combinat.iet.template.twin_list_li(a=None)¶

Returns the twin list of intervals

INPUT:

a - two lists of labels

OUTPUT:

list – a list of two lists of couples of integers

TESTS:

sage: from sage.combinat.iet.template import twin_list_li
sage: twin_list_li([['a','a','b','b'],[]])
[[(0, 1), (0, 0), (0, 3), (0, 2)], []]
sage: twin_list_li([['a','a','b'],['b']])
[[(0, 1), (0, 0), (1, 0)], [(0, 2)]]
sage: twin_list_li([['a','a'],['b','b']])
[[(0, 1), (0, 0)], [(1, 1), (1, 0)]]
sage: twin_list_li([['a'], ['a','b','b']])
[[(1, 0)], [(0, 0), (1, 2), (1, 1)]]
sage: twin_list_li([[], ['a','a','b','b']])
[[], [(1, 1), (1, 0), (1, 3), (1, 2)]]

Permutations template¶

Previous topic

Next topic

This Page

Navigation

Permutations template¶

Previous topic

Next topic

This Page

Quick search

Navigation