Interval Exchange Transformations and Linear Involution

An interval exchage transformation is a map defined on an interval (see help(iet.IntervalExchangeTransformation) for a more complete help.

EXAMPLES:

Initialization of a simple iet with integer lengths:

sage: T = iet.IntervalExchangeTransformation(Permutation([3,2,1]), [3,1,2])
sage: print T
Interval exchange transformation of [0, 6[ with permutation
1 2 3
3 2 1

Rotation corresponds to iet with two intervals:

sage: p = iet.Permutation('a b', 'b a')
sage: T = iet.IntervalExchangeTransformation(p, [1, (sqrt(5)-1)/2])
sage: print T.in_which_interval(0)
a
sage: print T.in_which_interval(T(0))
a
sage: print T.in_which_interval(T(T(0)))
b
sage: print T.in_which_interval(T(T(T(0))))
a

There are two plotting methods for iet:

sage: p = iet.Permutation('a b c','c b a')
sage: T = iet.IntervalExchangeTransformation(p, [1, 2, 3])

class sage.combinat.iet.iet.IntervalExchangeTransformation(permutation=None, lengths=None)

Bases: sage.structure.sage_object.SageObject

Interval exchange transformation

INPUT:

• permutation - a permutation (LabelledPermutationIET)
• lengths - the list of lengths

EXAMPLES:

Direct initialization:

sage: p = iet.IET(('a b c','c b a'),{'a':1,'b':1,'c':1})
sage: p.permutation()
a b c
c b a
sage: p.lengths()
[1, 1, 1]

Initialization from a iet.Permutation:

sage: perm = iet.Permutation('a b c','c b a')
sage: l = [0.5,1,1.2]
sage: t = iet.IET(perm,l)
sage: t.permutation() == perm
True
sage: t.lengths() == l
True

Initialization from a Permutation:

sage: p = Permutation([3,2,1])
sage: iet.IET(p, [1,1,1])
Interval exchange transformation of [0, 3[ with permutation
1 2 3
3 2 1

If it is not possible to convert lengths to real values an error is raised:

sage: iet.IntervalExchangeTransformation(('a b','b a'),['e','f'])
...
TypeError: unable to convert x (='e') into a real number

The value for the lengths must be positive:

sage: iet.IET(('a b','b a'),[-1,-1])
...
ValueError: lengths must be positive

domain_singularities()

Returns the list of singularities of T

OUTPUT:

list – positive reals that corresponds to singularities in the top

interval

EXAMPLES:

sage: t = iet.IET(("a b","b a"), [1, sqrt(2)])
sage: t.domain_singularities()
[0, 1, sqrt(2) + 1]

in_which_interval(x, interval=0)

Returns the letter for which x is in this interval.

INPUT:

• x - a positive number
• interval - (default: ‘top’) ‘top’ or ‘bottom’

OUTPUT:

label – a label corresponding to an interval

TEST:

sage: t = iet.IntervalExchangeTransformation(('a b c','c b a'),[1,1,1])
sage: t.in_which_interval(0)
'a'
sage: t.in_which_interval(0.3)
'a'
sage: t.in_which_interval(1)
'b'
sage: t.in_which_interval(1.9)
'b'
sage: t.in_which_interval(2)
'c'
sage: t.in_which_interval(2.1)
'c'
sage: t.in_which_interval(3)
...
ValueError: your value does not lie in [0;l[

inverse()

Returns the inverse iet.

OUTPUT:

iet – the inverse interval exchange transformation

EXAMPLES:

sage: p = iet.Permutation("a b","b a")
sage: s = iet.IET(p, [1,sqrt(2)-1])
sage: t = s.inverse()
sage: t.permutation()
b a
a b
sage: t.lengths()
[1, sqrt(2) - 1]
sage: t*s
Interval exchange transformation of [0, sqrt(2)[ with permutation
aa bb
aa bb

We can verify with the method .is_identity():

sage: p = iet.Permutation("a b c d","d a c b")
sage: s = iet.IET(p, [1, sqrt(2), sqrt(3), sqrt(5)])
sage: (s * s.inverse()).is_identity()
True
sage: (s.inverse() * s).is_identity()
True

is_identity()

Returns True if self is the identity.

OUTPUT:

boolean – the answer

EXAMPLES:

sage: p = iet.Permutation("a b","b a")
sage: q = iet.Permutation("c d","d c")
sage: s = iet.IET(p, [1,5])
sage: t = iet.IET(q, [5,1])
sage: (s*t).is_identity()
True
sage: (t*s).is_identity()
True

length()

Returns the total length of the interval.

OUTPUT:

real – the length of the interval

EXAMPLES:

sage: t = iet.IntervalExchangeTransformation(('a b','b a'),[1,1])
sage: t.length()
2

lengths()

Returns the list of lengths associated to this iet.

OUTPUT:

list – the list of lengths of subinterval

EXAMPLES:

sage: p = iet.IntervalExchangeTransformation(('a b','b a'),[1,3])
sage: p.lengths()
[1, 3]

normalize(total=1)

Returns a interval exchange transformation of normalized lengths.

The normalization consist in consider a constant homothetic value for each lengths in such way that the sum is given (default is 1).

INPUT:

• total - (default: 1) The total length of the interval

OUTPUT:

iet – the normalized iet

EXAMPLES:

sage: t = iet.IntervalExchangeTransformation(('a b','b a'), [1,3])
sage: t.length()
4
sage: s = t.normalize(2)
sage: s.length()
2
sage: s.lengths()
[1/2, 3/2]

permutation()

Returns the permutation associated to this iet.

OUTPUT:

permutation – the permutation associated to this iet

EXAMPLES:

sage: perm = iet.Permutation('a b c','c b a')
sage: p = iet.IntervalExchangeTransformation(perm,(1,2,1))
sage: p.permutation() == perm
True

plot(position=(0, 0), vertical_alignment='center', horizontal_alignment='left', interval_height=0.10000000000000001, labels_height=0.050000000000000003, fontsize=14, labels=True, colors=None)

Returns a picture of the interval exchange transformation.

INPUT:

• position - a 2-uple of the position
• horizontal_alignment - left (defaut), center or right
• labels - boolean (defaut: True)
• fontsize - the size of the label

OUTPUT:

2d plot – a plot of the two intervals (domain and range)

EXAMPLES:

sage: t = iet.IntervalExchangeTransformation(('a b','b a'),[1,1])
sage: t.plot_two_intervals()

plot_function(**d)

Return a plot of the interval exchange transformation as a function.

INPUT:

• Any option that is accepted by line2d

OUTPUT:

2d plot – a plot of the iet as a function

EXAMPLES:

sage: t = iet.IntervalExchangeTransformation(('a b c d','d a c b'),[1,1,1,1])
sage: t.plot_function(rgbcolor=(0,1,0))

plot_two_intervals(position=(0, 0), vertical_alignment='center', horizontal_alignment='left', interval_height=0.10000000000000001, labels_height=0.050000000000000003, fontsize=14, labels=True, colors=None)

Returns a picture of the interval exchange transformation.

INPUT:

• position - a 2-uple of the position
• horizontal_alignment - left (defaut), center or right
• labels - boolean (defaut: True)
• fontsize - the size of the label

OUTPUT:

2d plot – a plot of the two intervals (domain and range)

EXAMPLES:

sage: t = iet.IntervalExchangeTransformation(('a b','b a'),[1,1])
sage: t.plot_two_intervals()

range_singularities()

Returns the list of singularities of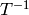

OUTPUT:

list – real numbers that are singular for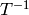

EXAMPLES:

sage: t = iet.IET(("a b","b a"), [1, sqrt(2)])
sage: t.range_singularities()
[0, sqrt(2), sqrt(2) + 1]

rauzy_move(side='right', iterations=1)

Performs a Rauzy move.

INPUT:

• side - ‘left’ (or ‘l’ or 0) or ‘right’ (or ‘r’ or 1)

• iterations - integer (default :1) the number of iteration of Rauzy

  moves to perform

OUTPUT:

iet – the Rauzy move of self

EXAMPLES:

sage: phi = QQbar((sqrt(5)-1)/2)
sage: t1 = iet.IntervalExchangeTransformation(('a b','b a'),[1,phi])
sage: t2 = t1.rauzy_move().normalize(t1.length())
sage: l2 = t2.lengths() 
sage: l1 = t1.lengths()
sage: l2[0] == l1[1] and l2[1] == l1[0]
True

show()

Shows a picture of the interval exchange transformation

EXAMPLES:

sage: phi = QQbar((sqrt(5)-1)/2)
sage: t = iet.IntervalExchangeTransformation(('a b','b a'),[1,phi])
sage: t.show()

singularities()

The list of singularities of ‘T’ and ‘T^{-1}’.

OUTPUT:

list – two lists of positive numbers which corresponds to extremities

of subintervals

EXAMPLE:

sage: t = iet.IntervalExchangeTransformation(('a b','b a'),[1/2,3/2])
sage: t.singularities()
[[0, 1/2, 2], [0, 3/2, 2]]