Hecke modules

class sage.categories.hecke_modules.HeckeModules(R)

Bases: sage.categories.category_types.Category_module

The category of Hecke modules.

A Hecke module is a module over the emph{anemic} Hecke algebra, i.e., the Hecke algebra generated by Hecke operators 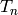with coprime to the level of . (Every Hecke module defines a level function, which is a positive integer.) The reason we require that only be a module over the anemic Hecke algebra is that many natural maps, e.g., degeneracy maps, Atkin-Lehner operators, etc., are 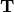-module homomorphisms; but they are homomorphisms over the anemic Hecke algebra.

EXAMPLES:

We create the category of Hecke modules over :

sage: C = HeckeModules(RationalField()); C
Category of Hecke modules over Rational Field

TODO: check that this is what we want:

sage: C.super_categories()
[Category of modules with basis over Rational Field]

# [Category of vector spaces over Rational Field]

Note that the base ring can be an arbitrary commutative ring:

sage: HeckeModules(IntegerRing())
Category of Hecke modules over Integer Ring
sage: HeckeModules(FiniteField(5))
Category of Hecke modules over Finite Field of size 5

The base ring doesn’t have to be a principal ideal domain:

sage: HeckeModules(PolynomialRing(IntegerRing(), 'x'))
Category of Hecke modules over Univariate Polynomial Ring in x over Integer Ring

TESTS:

sage: TestSuite(HeckeModules(ZZ)).run()

class HomCategory(category, name=None)

Bases: sage.categories.category.HomCategory

ParentMethods

alias of HomCategory.ParentMethods

extra_super_categories()

EXAMPLES:

sage: HeckeModules(ZZ).hom_category().extra_super_categories()
[]

HeckeModules.super_categories(*args, **kwds)

EXAMPLES:

sage: HeckeModules(QQ).super_categories()
[Category of modules with basis over Rational Field]