Finite Coxeter Groups

class sage.categories.finite_coxeter_groups.FiniteCoxeterGroups(s=None)

Bases: sage.categories.category.Category

The category of finite Coxeter groups.

EXAMPLES:

sage: FiniteSemigroups()
Category of finite semigroups
sage: FiniteSemigroups().super_categories()
[Category of semigroups, Category of finite enumerated sets]

sage: G = FiniteCoxeterGroups().example()
sage: G.cayley_graph(side = "right").plot()

Here are some further examples:

sage: FiniteWeylGroups().example()
The symmetric group on {0, ..., 3}

sage: WeylGroup(["B", 3])
Weyl Group of type ['B', 3] (as a matrix group acting on the ambient space)

Those other examples will eventually be also in this category:

sage: SymmetricGroup(4)
Symmetric group of order 4! as a permutation group
sage: DihedralGroup(5)
Dihedral group of order 10 as a permutation group

class ElementMethods

bruhat_upper_covers(*args, **kwds)

Returns all the elements that cover self in Bruhat order.

EXAMPLES:

sage: W = WeylGroup(["A",4])
sage: w = W.from_reduced_word([3,2])
sage: print([v.reduced_word() for v in w.bruhat_upper_covers()])
[[4, 3, 2], [3, 4, 2], [2, 3, 2], [3, 1, 2], [3, 2, 1]]

sage: W = WeylGroup(["B",6])
sage: w = W.from_reduced_word([1,2,1,4,5])
sage: C = w.bruhat_upper_covers()
sage: len(C)
9
sage: print([v.reduced_word() for v in C])
[[6, 4, 5, 1, 2, 1], [4, 5, 6, 1, 2, 1], [3, 4, 5, 1, 2, 1], [2, 3, 4, 5, 1, 2], 
[1, 2, 3, 4, 5, 1], [4, 5, 4, 1, 2, 1], [4, 5, 3, 1, 2, 1], [4, 5, 2, 3, 1, 2], 
[4, 5, 1, 2, 3, 1]]
sage: ww = W.from_reduced_word([5,6,5])
sage: CC = ww.bruhat_upper_covers()
sage: print([v.reduced_word() for v in CC])
[[6, 5, 6, 5], [4, 5, 6, 5], [5, 6, 4, 5], [5, 6, 5, 4], [5, 6, 5, 3], [5, 6, 5, 2], 
[5, 6, 5, 1]]

Recursive algorithm: write for self. If is a non-descent of 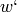, then the covers of are exactly .

class FiniteCoxeterGroups.ParentMethods

bruhat_poset(*args, **kwds)

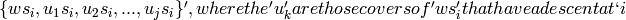Returns the Bruhat poset of self

EXAMPLES:

sage: W = WeylGroup(["A", 2])
sage: P = W.bruhat_poset()
sage: P
Finite poset containing 6 elements
sage: P.show()

Here are some typical operations on this poset:

sage: W = WeylGroup(["A", 3])
sage: P = W.bruhat_poset()
sage: u = W.from_reduced_word([3,1])
sage: v = W.from_reduced_word([3,2,1,2,3])
sage: P(u) <= P(v)
True
sage: len(P.interval(P(u), P(v)))
10
sage: P.is_join_semilattice()
False

See also Poset.

TESTS:

sage: [len(WeylGroup(["A", n]).bruhat_poset().cover_relations()) for n in [1,2,3]]
[1, 8, 58]

TODO:

• Use the symmetric group in the examples (for nicer output), and print the edges for a stronger test.
• The constructed poset should be lazy, in order to handle large / infinite Coxeter groups.

long_element(index_set=None)

INPUT:

• index_set - a subset (as a list or iterable) of the nodes of the dynkin diagram; (default: all of them)

Returns the longest element of self, or of the parabolic subgroup corresponding to the given index_set.

Should this method be called maximal_element? longest_element?

EXAMPLES:

sage: D10 = FiniteCoxeterGroups().example(10) 
sage: D10.long_element()
(1, 2, 1, 2, 1, 2, 1, 2, 1, 2)
sage: D10.long_element([1])
(1,)
sage: D10.long_element([2])
(2,)
sage: D10.long_element([])
()

sage: D7 = FiniteCoxeterGroups().example(7)   
sage: D7.long_element()                     
(1, 2, 1, 2, 1, 2, 1)

w0()

Return the longest element of self.

This attribute is deprecated.

EXAMPLES:

sage: D8 = FiniteCoxeterGroups().example(8)   
sage: D8.w0
(1, 2, 1, 2, 1, 2, 1, 2)
sage: D3 = FiniteCoxeterGroups().example(3) 
sage: D3.w0                                 
(1, 2, 1)

weak_poset(*args, **kwds)

INPUT:

• side – “left” or “right” (default: “right”)

Returns the left (resp. right) poset for weak order. In this poset, is smaller than if some reduced word of is a right (resp. left) factor of some reduced word of .

EXAMPLES:

sage: W = WeylGroup(["A", 2])
sage: P = W.weak_poset()
sage: P
Finite poset containing 6 elements
sage: P.show()

This poset is in fact a lattice:

sage: W = WeylGroup(["B", 3])
sage: P = W.weak_poset(side = "left")
sage: P.is_join_semilattice(), P.is_meet_semilattice() # todo: implement is_lattice
(True, True)

As a bonus feature, one can create the left-right weak poset:

sage: W = WeylGroup(["A",2])
sage: P = W.weak_poset(side = "twosided")
sage: P.show()
sage: len(P.hasse_diagram().edges())
8

This is the transitive closure of the union of left and right order. In this poset, is smaller than if some reduced word of is a factor of some reduced word of .

TESTS:

sage: [len(WeylGroup(["A", n]).weak_poset(side = "right").cover_relations()) for n in [1,2,3]]
[1, 6, 36]
sage: [len(WeylGroup(["A", n]).weak_poset(side = "left" ).cover_relations()) for n in [1,2,3]]
[1, 6, 36]

TODO:

• Use the symmetric group in the examples (for nicer output), and print the edges for a stronger test.
• The constructed poset should be lazy, in order to handle large / infinite Coxeter groups.

FiniteCoxeterGroups.super_categories(*args, **kwds)

EXAMPLES:

sage: FiniteCoxeterGroups().super_categories()
[Category of coxeter groups, Category of finite groups]