CommutativeAdditiveMonoids

class sage.categories.commutative_additive_monoids.CommutativeAdditiveMonoids(s=None)

Bases: sage.categories.category.Category

The category of abelian monoids semigroups with an additive identity element

EXAMPLES:

sage: CommutativeAdditiveMonoids()
Category of commutative additive monoids
sage: CommutativeAdditiveMonoids().super_categories()
[Category of commutative additive semigroups]
sage: CommutativeAdditiveMonoids().all_super_categories()
[Category of commutative additive monoids, Category of commutative additive semigroups, Category of additive magmas, Category of sets, Category of sets with partial maps, Category of objects]

TESTS:

sage: TestSuite(CommutativeAdditiveMonoids()).run()

class ElementMethods

class CommutativeAdditiveMonoids.ParentMethods

sum(args)

n-ary sum

INPUT:

• args – a list (or iterable) of elements of self

Returns the sum of the elements in 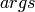, as an element of .

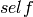EXAMPLES:

sage: S = CommutativeAdditiveMonoids().example()
sage: (a,b,c,d) = S.additive_semigroup_generators()
sage: S.sum((a,b,a,c,a,b))
3*a + c + 2*b
sage: S.sum(())
0
sage: S.sum(()).parent() == S
True

zero(*args, **kwds)

Returns the zero of the abelian monoid, that is the unique neutral element for .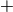

The default implementation is to coerce 0 into self.

It is recommended to override this method because the coercion from the integers:

• is not always meaningful (except for ),
• often uses self.zero() otherwise.

EXAMPLES:

sage: S = CommutativeAdditiveMonoids().example()
sage: S.zero()
0

zero_element()

Backward compatibility alias for self.zero()

TESTS:

sage: S = CommutativeAdditiveMonoids().example()
sage: S.zero_element()
0

CommutativeAdditiveMonoids.super_categories(*args, **kwds)

EXAMPLES:

sage: CommutativeAdditiveMonoids().super_categories()
[Category of commutative additive semigroups]