Bimodules

class sage.categories.bimodules.Bimodules(left_base, right_base, name=None)

Bases: sage.categories.category.Category

The category of 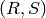-bimodules

For and rings, a 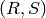-bimodule is a left -module and right -module such that the left and right actions commute: .

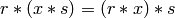EXAMPLES:

sage: Bimodules(QQ, ZZ)
Category of bimodules over Rational Field on the left and Integer Ring on the right
sage: Bimodules(QQ, ZZ).super_categories()
[Category of left modules over Rational Field, Category of right modules over Integer Ring]

class ElementMethods

class Bimodules.ParentMethods

classmethod Bimodules.an_instance()

Returns an instance of this class

EXAMPLES:

sage: Bimodules.an_instance()
Category of bimodules over Rational Field on the left and Real Field with 53 bits of precision on the right

Bimodules.left_base_ring()

Returns the left base ring over which elements of this category are defined.

EXAMPLES:

sage: Bimodules(QQ, ZZ).left_base_ring()
Rational Field

Bimodules.right_base_ring()

Returns the right base ring over which elements of this category are defined.

EXAMPLES:

sage: Bimodules(QQ, ZZ).right_base_ring()
Integer Ring

Bimodules.super_categories(*args, **kwds)

EXAMPLES:

sage: Bimodules(QQ, ZZ).super_categories()
[Category of left modules over Rational Field, Category of right modules over Integer Ring]