This file contains functions useful for solving differential equations which occur commonly in a 1st semester differential equations course. For another numerical solver see ode_solver() function and optional package Octave.
Commands:
AUTHORS:
Solves a 1st or 2nd order linear ODE via maxima. Including IVP and BVP.
Use desolve? <tab> if the output in truncated in notebook.
INPUT:
OUTPUT:
In most cases returns SymbolicEquation which defines the solution implicitly. If the result is in the form y(x)=... (happens for linear eqs.), returns the right-hand side only. The possible constant solutions of separable ODE’s are omitted.
EXAMPLES:
sage: x = var('x')
sage: y = function('y', x)
sage: desolve(diff(y,x) + y - 1, y)
(c + e^x)*e^(-x)
sage: f = desolve(diff(y,x) + y - 1, y, ics=[10,2]); f
(e^10 + e^x)*e^(-x)
sage: plot(f)
We can also solve second-order differential equations.:
sage: x = var('x')
sage: y = function('y', x)
sage: de = diff(y,x,2) - y == x
sage: desolve(de, y)
k1*e^x + k2*e^(-x) - x
sage: f = desolve(de, y, [10,2,1]); f
-x + 5*e^(-x + 10) + 7*e^(x - 10)
sage: f(x=10)
2
sage: diff(f,x)(x=10)
1
sage: de = diff(y,x,2) + y == 0
sage: desolve(de, y)
k1*sin(x) + k2*cos(x)
sage: desolve(de, y, [0,1,pi/2,4])
4*sin(x) + cos(x)
sage: desolve(y*diff(y,x)+sin(x)==0,y)
-1/2*y(x)^2 == c - cos(x)
Clairot equation: general and singular solutions:
sage: desolve(diff(y,x)^2+x*diff(y,x)-y==0,y,contrib_ode=True,show_method=True)
[[y(x) == c^2 + c*x, y(x) == -1/4*x^2], 'clairault']
For equations involving more variables we specify independent variable:
sage: a,b,c,n=var('a b c n')
sage: desolve(x^2*diff(y,x)==a+b*x^n+c*x^2*y^2,y,ivar=x,contrib_ode=True)
[[y(x) == 0, (b*x^(n - 2) + a/x^2)*c^2*u == 0]]
sage: desolve(x^2*diff(y,x)==a+b*x^n+c*x^2*y^2,y,ivar=x,contrib_ode=True,show_method=True)
[[[y(x) == 0, (b*x^(n - 2) + a/x^2)*c^2*u == 0]], 'riccati']
Higher orded, not involving independent variable:
sage: desolve(diff(y,x,2)+y*(diff(y,x,1))^3==0,y).expand()
1/6*y(x)^3 + k1*y(x) == k2 + x
sage: desolve(diff(y,x,2)+y*(diff(y,x,1))^3==0,y,[0,1,1,3]).expand()
1/6*y(x)^3 - 5/3*y(x) == x - 3/2
sage: desolve(diff(y,x,2)+y*(diff(y,x,1))^3==0,y,[0,1,1,3],show_method=True)
[1/6*y(x)^3 - 5/3*y(x) == x - 3/2, 'freeofx']
Separable equations - Sage returns solution in implicit form:
sage: desolve(diff(y,x)*sin(y) == cos(x),y)
-cos(y(x)) == c + sin(x)
sage: desolve(diff(y,x)*sin(y) == cos(x),y,show_method=True)
[-cos(y(x)) == c + sin(x), 'separable']
sage: desolve(diff(y,x)*sin(y) == cos(x),y,[pi/2,1])
-cos(y(x)) == sin(x) - cos(1) - 1
Linear equation - Sage returns the expression on the right hand side only:
sage: desolve(diff(y,x)+(y) == cos(x),y)
1/2*((sin(x) + cos(x))*e^x + 2*c)*e^(-x)
sage: desolve(diff(y,x)+(y) == cos(x),y,show_method=True)
[1/2*((sin(x) + cos(x))*e^x + 2*c)*e^(-x), 'linear']
sage: desolve(diff(y,x)+(y) == cos(x),y,[0,1])
1/2*(e^x*sin(x) + e^x*cos(x) + 1)*e^(-x)
This ODE with separated variables is solved as
exact. Explanation - factor does not split 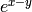 in Maxima
into
in Maxima
into 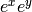 :
:
sage: desolve(diff(y,x)==exp(x-y),y,show_method=True)
[-e^x + e^y(x) == c, 'exact']
You can solve Bessel equations. You can also use initial conditions, but you cannot put (sometimes desired) initial condition at x=0, since this point is singlar point of the equation. Anyway, if the solution should be bounded at x=0, then k2=0.:
sage: desolve(x^2*diff(y,x,x)+x*diff(y,x)+(x^2-4)*y==0,y)
k1*bessel_j(2, x) + k2*bessel_y(2, x)
Difficult ODE produces error:
sage: desolve(sqrt(y)*diff(y,x)+e^(y)+cos(x)-sin(x+y)==0,y) # not tested
Traceback (click to the left for traceback)
...
NotImplementedError, "Maxima was unable to solve this ODE. Consider to set option contrib_ode to True."
Difficult ODE produces error - moreover, takes a long time
sage: desolve(sqrt(y)*diff(y,x)+e^(y)+cos(x)-sin(x+y)==0,y,contrib_ode=True) # not tested
Some more types od ODE’s:
sage: desolve(x*diff(y,x)^2-(1+x*y)*diff(y,x)+y==0,y,contrib_ode=True,show_method=True)
[[y(x) == c + log(x), y(x) == c*e^x], 'factor']
sage: desolve(diff(y,x)==(x+y)^2,y,contrib_ode=True,show_method=True)
[[[x == c - arctan(sqrt(t)), y(x) == -x - sqrt(t)], [x == c + arctan(sqrt(t)), y(x) == -x + sqrt(t)]], 'lagrange']
These two examples produce error (as expected, Maxima 5.18 cannot solve equations from initial conditions). Current Maxima 5.18 returns false answer in this case!:
sage: desolve(diff(y,x,2)+y*(diff(y,x,1))^3==0,y,[0,1,2]).expand() # not tested
Traceback (click to the left for traceback)
...
NotImplementedError, "Maxima was unable to solve this ODE. Consider to set option contrib_ode to True."
sage: desolve(diff(y,x,2)+y*(diff(y,x,1))^3==0,y,[0,1,2],show_method=True) # not tested
Traceback (click to the left for traceback)
...
NotImplementedError, "Maxima was unable to solve this ODE. Consider to set option contrib_ode to True."
Second order linear ODE:
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == cos(x),y)
(k2*x + k1)*e^(-x) + 1/2*sin(x)
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == cos(x),y,show_method=True)
[(k2*x + k1)*e^(-x) + 1/2*sin(x), 'variationofparameters']
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == cos(x),y,[0,3,1])
1/2*(7*x + 6)*e^(-x) + 1/2*sin(x)
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == cos(x),y,[0,3,1],show_method=True)
[1/2*(7*x + 6)*e^(-x) + 1/2*sin(x), 'variationofparameters']
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == cos(x),y,[0,3,pi/2,2])
3*((e^(1/2*pi) - 2)*x/pi + 1)*e^(-x) + 1/2*sin(x)
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == cos(x),y,[0,3,pi/2,2],show_method=True)
[3*((e^(1/2*pi) - 2)*x/pi + 1)*e^(-x) + 1/2*sin(x), 'variationofparameters']
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == 0,y)
(k2*x + k1)*e^(-x)
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == 0,y,show_method=True)
[(k2*x + k1)*e^(-x), 'constcoeff']
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == 0,y,[0,3,1])
(4*x + 3)*e^(-x)
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == 0,y,[0,3,1],show_method=True)
[(4*x + 3)*e^(-x), 'constcoeff']
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == 0,y,[0,3,pi/2,2])
(2*(2*e^(1/2*pi) - 3)*x/pi + 3)*e^(-x)
sage: desolve(diff(y,x,2)+2*diff(y,x)+y == 0,y,[0,3,pi/2,2],show_method=True)
[(2*(2*e^(1/2*pi) - 3)*x/pi + 3)*e^(-x), 'constcoeff']
This equation can be solved within Maxima but not within Sage. It needs assumptions assume(x>0,y>0) and works in Maxima, but not in Sage:
sage: assume(x>0) # not tested
sage: assume(y>0) # not tested
sage: desolve(x*diff(y,x)-x*sqrt(y^2+x^2)-y,y,show_method=True) # not tested
TESTS:
Trac #6479 fixed:
sage: x = var('x')
sage: y = function('y', x)
sage: desolve( diff(y,x,x) == 0, y, [0,0,1])
x
sage: desolve( diff(y,x,x) == 0, y, [0,1,1])
x + 1
AUTHORS:
Solves an ODE using laplace transforms. Initials conditions are optional.
INPUT:
OUTPUT:
Solution of the ODE as symbolic expression
EXAMPLES:
sage: u=function('u',x)
sage: eq = diff(u,x) - exp(-x) - u == 0
sage: desolve_laplace(eq,u)
1/2*(2*u(0) + 1)*e^x - 1/2*e^(-x)
We can use initial conditions:
sage: desolve_laplace(eq,u,ics=[0,3])
-1/2*e^(-x) + 7/2*e^x
The initial conditions do not persist in the system (as they persisted in previous versions):
sage: desolve_laplace(eq,u)
1/2*(2*u(0) + 1)*e^x - 1/2*e^(-x)
sage: f=function('f', x)
sage: eq = diff(f,x) + f == 0
sage: desolve_laplace(eq,f,[0,1])
e^(-x)
sage: x = var('x')
sage: f = function('f', x)
sage: de = diff(f,x,x) - 2*diff(f,x) + f
sage: desolve_laplace(de,f)
-x*e^x*f(0) + x*e^x*D[0](f)(0) + e^x*f(0)
sage: desolve_laplace(de,f,ics=[0,1,2])
x*e^x + e^x
TESTS:
Trac #4839 fixed:
sage: t=var('t')
sage: x=function('x', t)
sage: soln=desolve_laplace(diff(x,t)+x==1, x, ics=[0,2])
sage: soln
e^(-t) + 1
sage: soln(t=3)
e^(-3) + 1
AUTHORS:
Solves numerically one first-order ordinary differential equation. See also ode_solver.
INPUT:
input is similar to desolve command. The differential equation can be written in a form close to the plot_slope_field or desolve command
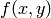 from ODE
from ODE 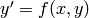
OUTPUT:
Returns a list of points, or plot produced by list_plot, optionally with slope field.
EXAMPLES:
sage: from sage.calculus.desolvers import desolve_rk4
Variant 2 for input - more common in numerics:
sage: x,y=var('x y')
sage: desolve_rk4(x*y*(2-y),y,ics=[0,1],end_points=1,step=0.5)
[[0, 1], [0.5, 1.12419127425], [1.0, 1.46159016229]]
Variant 1 for input - we can pass ODE in the form used by desolve function In this example we integrate bakwards, since end_points < ics[0]:
sage: y=function('y',x)
sage: desolve_rk4(diff(y,x)+y*(y-1) == x-2,y,ics=[1,1],step=0.5, end_points=0)
[[0.0, 8.90425710896], [0.5, 1.90932794536], [1, 1]]
Here we show how to plot simple pictures. For more advanced aplications use list_plot instead. To see the resulting picture use show(P) in Sage notebook.
sage: x,y=var('x y')
sage: P=desolve_rk4(y*(2-y),y,ics=[0,.1],ivar=x,output='slope_field',end_points=[-4,6],thickness=3)
ALGORITHM:
4th order Runge-Kutta method. Wrapper for command rk in Maxima’s dynamics package. Perhaps could be faster by using fast_float instead.
AUTHORS:
Used to determine bounds for numerical integration.
EXAMPLES:
sage: from sage.calculus.desolvers import desolve_rk4_determine_bounds
sage: desolve_rk4_determine_bounds([0,2],1)
(0, 1)
sage: desolve_rk4_determine_bounds([0,2])
(0, 10)
sage: desolve_rk4_determine_bounds([0,2],[-2])
(-2, 0)
sage: desolve_rk4_determine_bounds([0,2],[-2,4])
(-2, 4)
Solves any size system of 1st order ODE’s. Initials conditions are optional.
INPUT:
EXAMPLES:
sage: t = var('t')
sage: x = function('x', t)
sage: y = function('y', t)
sage: de1 = diff(x,t) + y - 1 == 0
sage: de2 = diff(y,t) - x + 1 == 0
sage: desolve_system([de1, de2], [x,y])
[x(t) == (x(0) - 1)*cos(t) - (y(0) - 1)*sin(t) + 1,
y(t) == (x(0) - 1)*sin(t) + (y(0) - 1)*cos(t) + 1]
Now we give some initial conditions:
sage: sol = desolve_system([de1, de2], [x,y], ics=[0,1,2]); sol
[x(t) == -sin(t) + 1, y(t) == cos(t) + 1]
sage: solnx, solny = sol[0].rhs(), sol[1].rhs()
sage: plot([solnx,solny],(0,1))
sage: parametric_plot((solnx,solny),(0,1))
AUTHORS:
Solves numerically system of first-order ordinary differential equations using the 4th order Runge-Kutta method. Wrapper for Maxima command rk. See also ode_solver.
INPUT:
input is similar to desolve_system and desolve_rk4 commands
OUTPUT:
Returns a list of points.
EXAMPLES:
sage: from sage.calculus.desolvers import desolve_system_rk4
Lotka Volterra system:
sage: from sage.calculus.desolvers import desolve_system_rk4
sage: x,y,t=var('x y t')
sage: P=desolve_system_rk4([x*(1-y),-y*(1-x)],[x,y],ics=[0,0.5,2],ivar=t,end_points=20)
sage: Q=[ [i,j] for i,j,k in P]
sage: LP=list_plot(Q)
sage: Q=[ [j,k] for i,j,k in P]
sage: LP=list_plot(Q)
ALGORITHM:
4th order Runge-Kutta method. Wrapper for command rk in Maxima’s dynamics package. Perhaps could be faster by using fast_float instead.
AUTHOR:
Solves any size system of 1st order ODE’s. Initials conditions are optional.
This function is obsolete, use desolve_system.
INPUT:
WARNING:
The given ics sets the initial values of the dependent vars in maxima, so subsequent ODEs involving these variables will have these initial conditions automatically imposed.
EXAMPLES:
sage: from sage.calculus.desolvers import desolve_system_strings
sage: s = var('s')
sage: function('x', s)
x(s)
sage: function('y', s)
y(s)
sage: de1 = lambda z: diff(z[0],s) + z[1] - 1
sage: de2 = lambda z: diff(z[1],s) - z[0] + 1
sage: des = [de1([x(s),y(s)]),de2([x(s),y(s)])]
sage: vars = ["s","x","y"]
sage: desolve_system_strings(des,vars)
["(1-'y(0))*sin(s)+('x(0)-1)*cos(s)+1", "('x(0)-1)*sin(s)+('y(0)-1)*cos(s)+1"]
sage: ics = [0,1,-1]
sage: soln = desolve_system_strings(des,vars,ics); soln
['2*sin(s)+1', '1-2*cos(s)']
sage: solnx, solny = map(SR, soln)
sage: RR(solnx(s=3))
1.28224001611973
sage: P1 = plot([solnx,solny],(0,1))
sage: P2 = parametric_plot((solnx,solny),(0,1))
Now type show(P1), show(P2) to view these.
AUTHORS:
This implements Euler’s method for finding numerically the solution of the 1st order ODE y' = f(x,y), y(a)=c. The “x” column of the table increments from x0 to x1 by h (so (x1-x0)/h must be an integer). In the “y” column, the new y-value equals the old y-value plus the corresponding entry in the last column.
For pedagogical purposes only.
EXAMPLES:
sage: from sage.calculus.desolvers import eulers_method
sage: x,y = PolynomialRing(QQ,2,"xy").gens()
sage: eulers_method(5*x+y-5,0,1,1/2,1)
x y h*f(x,y)
0 1 -2
1/2 -1 -7/4
1 -11/4 -11/8
sage: x,y = PolynomialRing(QQ,2,"xy").gens()
sage: eulers_method(5*x+y-5,0,1,1/2,1,method="none")
[[0, 1], [1/2, -1], [1, -11/4], [3/2, -33/8]]
sage: RR = RealField(sci_not=0, prec=4, rnd='RNDU')
sage: x,y = PolynomialRing(RR,2,"xy").gens()
sage: eulers_method(5*x+y-5,0,1,1/2,1,method="None")
[[0, 1], [1/2, -1.0], [1, -2.7], [3/2, -4.0]]
sage: RR = RealField(sci_not=0, prec=4, rnd='RNDU')
sage: x,y=PolynomialRing(RR,2,"xy").gens()
sage: eulers_method(5*x+y-5,0,1,1/2,1)
x y h*f(x,y)
0 1 -2.0
1/2 -1.0 -1.7
1 -2.7 -1.3
sage: x,y=PolynomialRing(QQ,2,"xy").gens()
sage: eulers_method(5*x+y-5,1,1,1/3,2)
x y h*f(x,y)
1 1 1/3
4/3 4/3 1
5/3 7/3 17/9
2 38/9 83/27
sage: eulers_method(5*x+y-5,0,1,1/2,1,method="none")
[[0, 1], [1/2, -1], [1, -11/4], [3/2, -33/8]]
sage: pts = eulers_method(5*x+y-5,0,1,1/2,1,method="none")
sage: P1 = list_plot(pts)
sage: P2 = line(pts)
sage: (P1+P2).show()
AUTHORS:
This implements Euler’s method for finding numerically the solution of the 1st order system of two ODEs
x' = f(t, x, y), x(t0)=x0.
y' = g(t, x, y), y(t0)=y0.
The “t” column of the table increments from 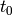 to
to 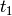 by
by 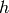 (so
(so 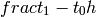 must be an integer). In the “x” column,
the new x-value equals the old x-value plus the corresponding
entry in the next (third) column. In the “y” column, the new
y-value equals the old y-value plus the corresponding entry in the
next (last) column.
must be an integer). In the “x” column,
the new x-value equals the old x-value plus the corresponding
entry in the next (third) column. In the “y” column, the new
y-value equals the old y-value plus the corresponding entry in the
next (last) column.
For pedagogical purposes only.
EXAMPLES:
sage: from sage.calculus.desolvers import eulers_method_2x2
sage: t, x, y = PolynomialRing(QQ,3,"txy").gens()
sage: f = x+y+t; g = x-y
sage: eulers_method_2x2(f,g, 0, 0, 0, 1/3, 1,method="none")
[[0, 0, 0], [1/3, 0, 0], [2/3, 1/9, 0], [1, 10/27, 1/27], [4/3, 68/81, 4/27]]
sage: eulers_method_2x2(f,g, 0, 0, 0, 1/3, 1)
t x h*f(t,x,y) y h*g(t,x,y)
0 0 0 0 0
1/3 0 1/9 0 0
2/3 1/9 7/27 0 1/27
1 10/27 38/81 1/27 1/9
sage: RR = RealField(sci_not=0, prec=4, rnd='RNDU')
sage: t,x,y=PolynomialRing(RR,3,"txy").gens()
sage: f = x+y+t; g = x-y
sage: eulers_method_2x2(f,g, 0, 0, 0, 1/3, 1)
t x h*f(t,x,y) y h*g(t,x,y)
0 0 0.00 0 0.00
1/3 0.00 0.13 0.00 0.00
2/3 0.13 0.29 0.00 0.043
1 0.41 0.57 0.043 0.15
To numerically approximate 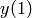 , where
, where 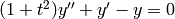 ,
,
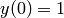 ,
, 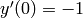 , using 4 steps of Euler’s method, first
convert to a system:
, using 4 steps of Euler’s method, first
convert to a system: 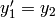 ,
, 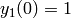 ;
; 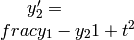 ,
, 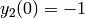 .:
.:
sage: RR = RealField(sci_not=0, prec=4, rnd='RNDU')
sage: t, x, y=PolynomialRing(RR,3,"txy").gens()
sage: f = y; g = (x-y)/(1+t^2)
sage: eulers_method_2x2(f,g, 0, 1, -1, 1/4, 1)
t x h*f(t,x,y) y h*g(t,x,y)
0 1 -0.25 -1 0.50
1/4 0.75 -0.12 -0.50 0.29
1/2 0.63 -0.054 -0.21 0.19
3/4 0.63 -0.0078 -0.031 0.11
1 0.63 0.020 0.079 0.071
To numerically approximate y(1), where 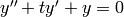 ,
, 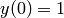 ,
, 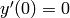 :
:
sage: t,x,y=PolynomialRing(RR,3,"txy").gens()
sage: f = y; g = -x-y*t
sage: eulers_method_2x2(f,g, 0, 1, 0, 1/4, 1)
t x h*f(t,x,y) y h*g(t,x,y)
0 1 0.00 0 -0.25
1/4 1.0 -0.062 -0.25 -0.23
1/2 0.94 -0.11 -0.46 -0.17
3/4 0.88 -0.15 -0.62 -0.10
1 0.75 -0.17 -0.68 -0.015
AUTHORS:
Plots solution of ODE
This plots the soln in the rectangle (xrange[0],xrange[1])
x (yrange[0],yrange[1]) and plots using Euler’s method the
numerical solution of the 1st order ODEs 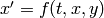 ,
,
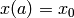 ,
, 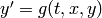 ,
, 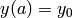 .
.
For pedagogical purposes only.
EXAMPLES:
sage: from sage.calculus.desolvers import eulers_method_2x2_plot
The following example plots the solution to
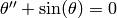 ,
, 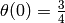 ,
, 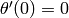 . Type P[0].show() to plot the solution,
(P[0]+P[1]).show() to plot
. Type P[0].show() to plot the solution,
(P[0]+P[1]).show() to plot 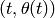 and
and
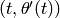 :
:
sage: f = lambda z : z[2]; g = lambda z : -sin(z[1])
sage: P = eulers_method_2x2_plot(f,g, 0.0, 0.75, 0.0, 0.1, 1.0)