Yes, a Sage job can be run in the background on a UNIX system. The canonical thing to do is type
nohup sage < command_file > output_file &
The advantage of nohup is that Sage will continue running after you log out.
Currently Sage will appear as “sage-ipython” or “python” in the output of the (unix) top command, but in future versions of Sage it will appears as sage.
To reference Sage, please add the following to your bibliography:
\bibitem[Sage]{sage}
Stein, William, \emph{Sage: {O}pen {S}ource {M}athematical {S}oftware
({V}ersion 2.10.2)}, The Sage~Group, 2008, {\tt http://www.sagemath.org}.
Here is the bibtex entry:
@manual{sage,
Key = {Sage},
Author = {William Stein},
Organization = {The Sage~Group},
Title = {{Sage}: {O}pen {S}ource {M}athematical {S}oftware ({V}ersion 2.10.2)},
Note= {{\tt http://www.sagemath.org}},
Year = 2008
}
If you happen to use the Sage interface to PARI, GAP or Singular, you should definitely reference them as well. Likewise, if you use code that is implemented using PARI, GAP, or Singular, reference the corresponding system (you can often tell from the documentation if PARI, GAP, or Singular is used in the implementation of a function).
For PARI, you may use
@manual{PARI2,
organization = "{The PARI~Group}",
title = "{PARI/GP, version {\tt 2.1.5}}",
year = 2004,
address = "Bordeaux",
note = "available from \url{http://pari.math.u-bordeaux.fr/}"
}
or
\bibitem{PARI2} PARI/GP, version {\tt 2.1.5}, Bordeaux, 2004,
\url{http://pari.math.u-bordeaux.fr/}.
(replace the version number by the one you used).
For GAP, you may use
[GAP04] The GAP Group, GAP -- Groups, Algorithms, and Programming,
Version 4.4; 2005. (http://www.gap-system.org)
or
@manual{GAP4,
key = "GAP",
organization = "The GAP~Group",
title = "{GAP -- Groups, Algorithms, and Programming,
Version 4.4}",
year = 2005,
note = "{\tt http://www.gap-system.org}",
keywords = "groups; *; gap; manual"}
\bibitem[GAP]{GAP4}
The GAP~Group, \emph{GAP -- Groups, Algorithms, and Programming, Version 4.4}; 2005,
{\tt http://www.gap-system.org}.
For Singular, you may use
[GPS05] G.-M. Greuel, G. Pfister, and H. Sch\"onemann.
{\sc Singular} 3.0. A Computer Algebra System for Polynomial
Computations. Centre for Computer Algebra, University of
Kaiserslautern (2005). {\tt http://www.singular.uni-kl.de}.
or
@TechReport{GPS05,
author = {G.-M. Greuel and G. Pfister and H. Sch\"onemann},
title = {{\sc Singular} 3.0},
type = {{A Computer Algebra System for Polynomial Computations}},
institution = {Centre for Computer Algebra},
address = {University of Kaiserslautern},
year = {2005},
note = {{\tt http://www.singular.uni-kl.de}},
}
or
\bibitem[GPS05]{GPS05}
G.-M.~Greuel, G.~Pfister, and H.~Sch\"onemann.
\newblock {{\sc Singular} 3.0}. A Computer Algebra System for Polynomial Computations.
\newblock Centre for Computer Algebra, University of Kaiserslautern (2005).
\newblock {\tt http://www.singular.uni-kl.de}.
Yes you can log your sessions.
(a) Modify line 186 of the .ipythonrc file (or open .ipythonrc into an editor and search for “logfile”). This will only log your input lines, not the output.
(b) You can also write the output to a file, by running Sage in the background ( Background jobs ).
(c) Start in a KDE konsole (this only work in linux). Go to
Settings 
History ... and select
unlimited. Start your session. When ready, go to edit
save history as ....
Some interfaces (such as the interface to Singular or that to GAP) allow you to create a log file. For Singular, there is a logfile option (in singular.py). In GAP, use the command LogTo.
Yes, you can output some of your results into LaTeX.
sage: M = MatrixSpace(RealField(),3,3)
sage: A = M([1,2,3, 4,5,6, 7,8,9])
sage: print latex(A)
\left(\begin{array}{rrr}
1.00000000000000 & 2.00000000000000 & 3.00000000000000 \\
4.00000000000000 & 5.00000000000000 & 6.00000000000000 \\
7.00000000000000 & 8.00000000000000 & 9.00000000000000
\end{array}\right)
sage: view(A)
At this point a dvi preview should automatically be called to display in a separate window the LaTeX output produced.
LaTeX previewing for multivariate polynomials and rational functions is also available:
sage: x = PolynomialRing(QQ,3, 'x').gens()
sage: f = x[0] + x[1] - 2*x[1]*x[2]
sage: h = f /(x[1] + x[2])
sage: print latex(h)
\frac{-2 x_{1} x_{2} + x_{0} + x_{1}}{x_{1} + x_{2}}
If foo is a Pari, GAP ( without ending semicolon), Singular, Maxima command, resp., enter gp("foo") for Pari, gap.eval("foo")} singular.eval("foo"), maxima("foo"), resp.. These programs merely send the command string to the external program, execute it, and read the result back into Sage. Therefore, these will not work if the external program is not installed and in your PATH.
If you know only part of the name of a Sage command and want to know where it occurs in Sage, a new option for 0.10.11 has been added to make it easier to hunt it down. Just type sage -grep <string> to find all occurences of <string> in the Sage source code. For example,
was@form:~/s/local/bin$ sage -grep berlekamp_massey
matrix/all.py:from berlekamp_massey import berlekamp_massey
matrix/berlekamp_massey.py:def berlekamp_massey(a):
matrix/matrix.py:import berlekamp_massey
matrix/matrix.py: g =
berlekamp_massey.berlekamp_massey(cols[i].list())
Type help(foo) or foo?? for help and foo.[tab] for searching of Sage commands. Type help() for Python commands.
For example
help(Matrix)
returns
Help on function Matrix in module sage.matrix.constructor:
Matrix(R, nrows, ncols, entries = 0, sparse = False)
Create a matrix.
INPUT:
R -- ring
nrows -- int; number of rows
ncols -- int; number of columns
entries -- list; entries of the matrix
sparse -- bool (default: False); whether or not to store matrices as sparse
OUTPUT:
a matrix
EXAMPLES:
sage: Matrix(RationalField(), 2, 2, [1,2,3,4])
[1 2]
[3 4]
sage: Matrix(FiniteField(5), 2, 3, range(6))
[0 1 2]
[3 4 0]
sage: Matrix(IntegerRing(), 10, 10, range(100)).parent()
Full MatrixSpace of 10 by 10 dense matrices over Integer Ring
sage: Matrix(IntegerRing(), 10, 10, range(100), sparse = True).parent()
Full MatrixSpace of 10 by 10 sparse matrices over Integer Ring
in a new screen. Type q to return to the Sage screen.
A file imported into Sage must end in .py, e.g., foo.py and contain legal Python syntax. For a simple example see Permutation groups with the Rubik’s cube group example above.
Another way to read a file in is to use the load or attach command. Create a file called example.sage (located in the home directory of Sage) with the following content:
print "Hello World"
print 2^3
Read in and execute example.sage file using the load command.
sage: load "example.sage"
Hello World
8
You can also attach a Sage file to a running session:
sage: attach "example.sage"
Hello World
8
Now if you change example.sage and enter one blank line into Sage, then the contents of example.sage will be automatically reloaded into Sage:
sage: !emacs example.sage& #change 2^3 to 2^4
sage: #hit return
***************************************************
Reloading 'example.sage'
***************************************************
Hello World
16
We shall explain the basic steps for installing the most recent version of Sage (which is the “source” version, not the “binary”).
Download sage-*.tar (where * denotes the version number) from the website and save into a directory, say HOME. Type tar zxvf sage-*.tar in HOME.
cd sage-* (we call this SAGE_ROOT) and type make. Now be patient because this process make take 2 hours or so.
Optional: When the compilation is finished, type on the command line in the Sage home directory:
./sage -i database_jones_numfield
./sage -i database_gap-4.4.8
./sage -i database_cremona_ellcurve-2005.11.03
./sage -i gap_packages-4.4.8_1
This last package loads the GAP GPL’d packages braid, ctbllib, DESIGN, FactInt, GAPDoc, GRAPE, LAGUNA, SONATA 2.3, and TORIC . It also compiles (automatically) the C programs in GUAVA and GRAPE.
Other optional packages to install are at http://modular.math.washington.edu/sage/packages/optional/.
Another way: download packages from http://sage.scipy.org/sage/packages/optional/ and save to the directory SAGE_ROOT. Type
/sage -i sage-package.spkg
for each sage-package you download (use sage -f if you are reinstalling.) This might be useful if you have a CD of these packages but no (or a very slow) internet connection.
If you want to build the documentation, cd devel/doc and type ./rebuild. This requires having latex and latex2html installed.
Let’s say you want to know what the Python program is for the Sage command to compute the center of a permutation group. Use Sage’s help interface to find the file name:
sage: PermutationGroup.center?
Type: instancemethod
Base Class: <type 'instancemethod'>
String Form: <unbound method PermutationGroup.center>
Namespace: Interactive
File: /home/wdj/sage/local/lib/python2.4/site-packages/sage/groups/permgroup.py
Definition: PermutationGroup.center(self)
Now you know that the command is located in the permgroup.py file and you know the directory to look for that Python module. You can use an editor to read the code itself.
Sage has several special functions:
and orthogonal polynomials
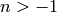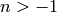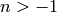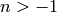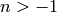.... and 
and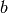 
symbolic or
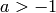and 
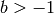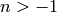.. The ultraspherical polynomials are also
known as Gegenbauer polynomials.In Sage, these are restricted to numerical evaluation and plotting but via maxima, some symbolic manipulation is allowed:
sage: maxima.eval("f:bessel_y (v, w)")
'bessel_y(v,w)'
sage: maxima.eval("diff(f,w)")
'(bessel_y(v-1,w)-bessel_y(v+1,w))/2'
sage: maxima.eval("diff (jacobi_sn (u, m), u)")
'jacobi_cn(u,m)*jacobi_dn(u,m)'
sage: jsn = lambda x: jacobi("sn",x,1)
sage: P = plot(jsn,0,1, plot_points=20); Q = plot(lambda x:bessel_Y( 1, x), 1/2,1)
sage: show(P)
sage: show(Q)
In addition to maxima, pari and octave also have special functions (in fact, some of pari‘s special functions are wrapped in Sage).
Here’s an example using Sage’s interface (located in sage/interfaces/octave.py) with octave (http://www.octave.org/doc/index.html).
sage: octave("atanh(1.1)") ## requires optional octave
(1.52226,-1.5708)
Here’s an example using Sage’s interface to pari‘s special functions.
sage: pari('2+I').besselk(3)
0.0455907718407551 + 0.0289192946582081*I
sage: pari('2').besselk(3)
0.0615104584717420
The last command can also be executed using the command
sage: bessel_K(3,2)
0.647385390948634
sage: bessel_K(3,2,prec=100)
0.64738539094863415315923557097
Sage is a framework for number theory, algebra, and geometry computation that is initially being designed for computing with elliptic curves and modular forms. The long-term goal is to make it much more generally useful for algebra, geometry, and number theory. It is open source and freely available under the terms of the GPL. The section titles in the reference manual gives a rough idea of the topics covered in Sage.
Sage was started by William Stein while at Harvard University in the Fall of 2004, with version 0.1 released in January of 2005. That version included Pari, but not GAP or Singular. Version 0.2 was released in March, version 0.3 in April, version 0.4 in July. During this time, support for Cremona’s database, multivariate polynomials and large finite fields was added. Also, more documentation was written. Version 0.5 beta was released in August, version 0.6 beta in September, and version 0.7 later that month. During this time, more support for vector spaces, rings, modular symbols, and windows users was added. As of 0.8, released in October 2005, Sage contained the full distribution of GAP, though some of the GAP databases have to be added separately, and Singular. Adding Singular was not easy, due to the difficulty of compiling Singular from source. Version 0.9 was released in November. This version went through 34 releases! As of version 0.9.34 (definitely by version 0.10.0), Maxima and clisp were included with Sage. Version 0.10.0 was released January 12, 2006. The release of Sage 1.0 was made early February, 2006. As of February 2008, the latest release is 2.10.2.
Many people have contributed significant code and other expertise, such as assistance in compiling on various OS’s. Generally code authors are acknowledged in the AUTHOR section of the Python docstring of their file and the credits section of the Sage website.