How do you count points on an elliptic curve over a finite field in Sage?
Over prime finite fields, includes both the the baby step giant step method, as implemented in PARI’s ellap, and the SEA (Schoof-Elkies-Atkin) algorithm as implemented in PARI by Christophe Doche and Sylvain Duquesne. An example taken form the Reference manual:
sage: E = EllipticCurve(GF(10007),[1,2,3,4,5])
sage: E.cardinality(algorithm='sea')
10076
sage: E.cardinality(algorithm='bsgs')
10076
The command E.points() will return the actual list of rational points.
How do you count points on a plane curve over a finite field? The rational_points command produces points by a simple enumeration algorithm. Here is an example of the syntax:
sage: x,y,z = PolynomialRing(GF(5), 3, 'xyz').gens()
sage: C = Curve(y^2*z^7 - x^9 - x*z^8); C
Projective Curve over Finite Field of size 5 defined by -x^9 + y^2*z^7 - x*z^8
sage: C.rational_points()
[(0 : 0 : 1), (0 : 1 : 0), (2 : 2 : 1), (2 : 3 : 1), (3 : 1 : 1), (3 : 4 : 1)]
sage: C.rational_points(algorithm="bn")
[(0 : 0 : 1), (0 : 1 : 0), (2 : 2 : 1), (2 : 3 : 1), (3 : 1 : 1), (3 : 4 : 1)]
The option algorithm="bn uses Sage’s Singular interface and calls the brnoeth package.
Here is another example using Sage’s rational_points applied to
Klein’s quartic over 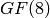 .
.
sage: x, y, z = PolynomialRing(GF(8,'a'), 3, 'xyz').gens()
sage: f = x^3*y+y^3*z+x*z^3
sage: C = Curve(f); C
Projective Curve over Finite Field in a of size 2^3 defined by x^3*y + y^3*z + x*z^3
sage: C.rational_points()
[(0 : 0 : 1),
(0 : 1 : 0),
(1 : 0 : 0),
(1 : a : 1),
(1 : a^2 : 1),
(1 : a^2 + a : 1),
(a : 1 : 1),
(a : a^2 : 1),
(a : a^2 + 1 : 1),
(a + 1 : a + 1 : 1),
(a + 1 : a^2 : 1),
(a + 1 : a^2 + a + 1 : 1),
(a^2 : 1 : 1),
(a^2 : a^2 + a : 1),
(a^2 : a^2 + a + 1 : 1),
(a^2 + 1 : a + 1 : 1),
(a^2 + 1 : a^2 + 1 : 1),
(a^2 + 1 : a^2 + a : 1),
(a^2 + a : 1 : 1),
(a^2 + a : a : 1),
(a^2 + a : a + 1 : 1),
(a^2 + a + 1 : a : 1),
(a^2 + a + 1 : a^2 + 1 : 1),
(a^2 + a + 1 : a^2 + a + 1 : 1)]
For a plane curve, you can use Singular’s closed_points
command. The input is the vanishing ideal 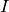 of the curve
of the curve
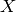 in a ring of
in a ring of 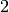 variables
variables ![F[x,y]](_images/math/b9eb5edcdbdd6de06f773186b906cd69e57a0fe7.png) .
The closed_points command returns a list of prime ideals (each a
Gröbner basis), corresponding to the (distinct affine closed)
points of
.
The closed_points command returns a list of prime ideals (each a
Gröbner basis), corresponding to the (distinct affine closed)
points of 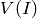 . Here’s an example:
. Here’s an example:
sage: singular_console()
SINGULAR / Development
A Computer Algebra System for Polynomial Computations / version 3-0-1
0<
by: G.-M. Greuel, G. Pfister, H. Schoenemann \ October 2005
FB Mathematik der Universitaet, D-67653 Kaiserslautern \
// ** executing /home/wdj/sagefiles/sage-0.9.4/local/LIB/.singularrc
> LIB "brnoeth.lib";
> ring s = 2,(x,y),lp;
> ideal I = x4+x,y4+y;
> list L = closed_points(I);
> L;
[1]:
_[1] = y
_[2] = x
[2]:
_[1] = y
_[2] = x+1
[3]:
_[1] = y
_[2] = x2+x+1
[4]:
_[1] = y+1
_[2] = x
[5]:
_[1] = y+1
_[2] = x+1
[6]:
_[1] = y+1
_[2] = x2+x+1
[7]:
_[1] = y2+y+1
_[2] = x+1
[8]:
_[1] = y2+y+1
_[2] = x
[9]:
_[1] = y2+y+1
_[2] = x+y
[10]:
_[1] = y2+y+1
_[2] = x+y+1
> Auf Wiedersehen.
sage: singular.lib("brnoeth.lib")
sage: s = singular.ring(2,'(x,y)','lp')
sage: I = singular.ideal('[x^4+x, y^4+y]')
sage: L = singular.closed_points(I)
sage: # Here you have all the points :
sage: print L
[1]:
_[1]=y^2+y+1
_[2]=x+1
...
Another way to compute rational points is to use Singular’s
NSplaces command. Here’s the Klein quartic over 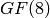 done this way:
done this way:
sage: singular.LIB("brnoeth.lib")
sage: s = singular.ring(2,'(x,y)','lp')
...
sage: f = singular.poly('x3y+y3+x')
...
sage: klein1 = f.Adj_div(); print klein1
[1]:
[1]:
// characteristic : 2
// number of vars : 2
// block 1 : ordering lp
// : names x y
// block 2 : ordering C
...
sage: # define a curve X = {f = 0} over GF(2)
sage: klein2 = singular.NSplaces(3,klein1)
sage: print singular.eval('extcurve(3,%s)'%klein2.name())
Total number of rational places : NrRatPl = 23
...
sage: klein3 = singular.extcurve(3, klein2)
Above we defined a curve 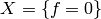 over
over
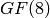 in Singular.
in Singular.
sage: print klein1
[1]:
[1]:
// characteristic : 2
// number of vars : 2
// block 1 : ordering lp
// : names x y
// block 2 : ordering C
[2]:
// characteristic : 2
// number of vars : 3
// block 1 : ordering lp
// : names x y z
// block 2 : ordering C
[2]:
4,3
[3]:
[1]:
1,1
[2]:
1,2
[4]:
0
[5]:
[1]:
[1]:
// characteristic : 2
// number of vars : 3
// block 1 : ordering ls
// : names x y t
// block 2 : ordering C
[2]:
1,1
sage: print klein1[3]
[1]:
1,1
[2]:
1,2
For the places of degree 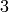 :
:
sage: print klein2[3]
[1]:
1,1
[2]:
1,2
[3]:
3,1
[4]:
3,2
[5]:
3,3
[6]:
3,4
[7]:
3,5
[8]:
3,6
[9]:
3,7
Each point below is a pair: (degree, point index number).
sage: print klein3[3]
[1]:
1,1
[2]:
1,2
[3]:
3,1
[4]:
3,2
[5]:
3,3
[6]:
3,4
[7]:
3,5
[8]:
3,6
[9]:
3,7
To actually get the points of 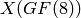 :
:
sage: R = klein3[1][5]
sage: R.set_ring()
sage: singular("POINTS;")
[1]:
[1]:
0
[2]:
1
[3]:
0
[2]:
[1]:
1
[2]:
0
[3]:
0
...
plus 21 others (omitted). There are a total of 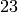 rational points.
rational points.
Can you compute a basis of a Riemann-Roch space in Sage?
Unfortunately, the answer is “no” at the present time. The version of Singular currently used by (version 3.0.2) has a Brill-Noether algorithm implementation (computing a basis of a Riemann-Roch space) which appears to be buggy. The rest of this section is included to illustrate the syntax once the bugs in brnoeth get worked out (or to help any developers wishing to work on this themselves).
To compute a basis for the Riemann-Roch space 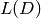 associated to a divisor
associated to a divisor 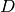 on a curve
on a curve 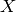 over a
field
over a
field 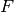 , you can use ‘s “wrapper” riemann_roch_basis
to Singular or Singular itself. Both are illustrated below.
, you can use ‘s “wrapper” riemann_roch_basis
to Singular or Singular itself. Both are illustrated below.
sage: x, y, z = PolynomialRing(GF(5), 3, 'xyz').gens()
sage: f = x^7 + y^7 + z^7
sage: C = Curve(f); pts = C.rational_points()
sage: D = C.divisor([ (3, pts[0]), (-1,pts[1]), (10, pts[5]) ])
sage: C.riemann_roch_basis(D)
[x^8*y/(x^6*z^3 - x^5*y*z^3 + ... # 32-bit
[(x^9 + x^8*y)/(x^6*z^3 - ... # 64-bit
The output is somewhat random.
Singular’s BrillNoether command (for details on this command, see the section Brill-Noether in the Singular online documentation (http://www.singular.uni-kl.de/Manual/html/sing_960.htm and the paper {CF}):
sage: singular.LIB('brnoeth.lib')
sage: _ = singular.ring(5,'(x,y)','lp')
sage: print singular.eval("list X = Adj_div(-x5+y2+x);")
Computing affine singular points ...
Computing all points at infinity ...
Computing affine singular places ...
Computing singular places at infinity ...
Computing non-singular places at infinity ...
Adjunction divisor computed successfully
<BLANKLINE>
The genus of the curve is 2
sage: print singular.eval("X = NSplaces(1..2,X);")
Computing non-singular affine places of degree 1 ...
Computing non-singular affine places of degree 2 ...
sage: print singular("X[3];")
[1]:
1,1
[2]:
1,2
[3]:
1,3
[4]:
1,4
[5]:
1,5
[6]:
1,6
The 6 Places in X[3] are of degree 1. We define the rational divisor {G = 4*C[3][1]+4*C[3][2]+4*C[3][3]} (of degree 12):
sage: singular.eval("intvec G = 4,4,4,0,0,0;")
'intvec G = 4,4,4,0,0,0;'
sage: singular.eval("def R = X[1][2];")
'def R = X[1][2];'
sage: singular.eval("setring R;")
'setring R;'
sage: print singular.eval("list LG = BrillNoether(G,X);")
Forms of degree 6 :
28
<BLANKLINE>
Vector basis successfully computed
<BLANKLINE>
Here is the vector basis of L(G):
sage: print singular.eval("LG;")
[1]: # 32-bit
_[1]=x2 # 32-bit
_[2]=x2+z2 # 32-bit
[2]: # 32-bit
_[1]=-x4+x2z2 # 32-bit
_[2]=x2y2+y2z2 # 32-bit
[1]: # 64-bit
_[1]=-x5+x4z-x3y2+2x3z2+x2y2z # 64-bit
_[2]=-x4z+x3y2+z5 # 64-bit
[2]: # 64-bit
_[1]=-2x5-x4z+2x3y2+2x3z2+x2z3 # 64-bit
_[2]=-x4z+x3y2+z5 # 64-bit
...
Sage can compute an AG code 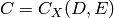 by calling
Singular’s BrillNoether to compute a basis of the Riemann Roch
space
by calling
Singular’s BrillNoether to compute a basis of the Riemann Roch
space 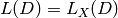 . In addition to the curve
. In addition to the curve 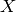 and the divisor
and the divisor 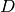 , you must also specify the evaluation
divisor
, you must also specify the evaluation
divisor 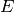 .
.
As in the previous section, until the bugs in brnoth are worked out, this section is only included to illustrate syntax (or to help any developers wishing to work on this themselves).
Here’s an example, one which computes a generator matrix of an associated AG code. This time we use Singular’s AGCode_L command.
sage: singular.LIB('brnoeth.lib')
sage: singular.eval("ring s = 2,(x,y),lp;")
'ring s = 2,(x,y),lp;'
sage: print singular.eval("list HC = Adj_div(x3+y2+y);")
Computing affine singular points ...
Computing all points at infinity ...
Computing affine singular places ...
Computing singular places at infinity ...
Computing non-singular places at infinity ...
Adjunction divisor computed successfully
<BLANKLINE>
The genus of the curve is 1
sage: print singular.eval("list HC1 = NSplaces(1..2,HC);")
Computing non-singular affine places of degree 1 ...
Computing non-singular affine places of degree 2 ...
sage: print singular.eval("HC = extcurve(2,HC1);")
Total number of rational places : NrRatPl = 9
We set the following to junk to discard the output:
sage: junk = singular.eval("intvec G = 5;") # the rational divisor G = 5*HC[3][1]
sage: junk = singular.eval("def R = HC[1][2];")
sage: singular.eval("setring R;")
'setring R;'
The vector 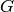 represents the divisor
“5 times the point at infinity”.
represents the divisor
“5 times the point at infinity”.
Next, we compute the Riemann-Roch space.
sage: print singular.eval("BrillNoether(G,HC);")
Forms of degree 3 :
10
<BLANKLINE>
Vector basis successfully computed
<BLANKLINE>
[1]:
_[1]=x
_[2]=z
[2]:
_[1]=y
_[2]=z
[3]:
_[1]=1
_[2]=1
[4]:
_[1]=y2+yz
_[2]=xz
[5]:
_[1]=y3+y2z
_[2]=x2z
That was the basis of the Riemann-Roch space, where each pair of fuctions represents the quotient (first function divided by second function). Each of these basis elements get evaluated at certain points to construct the generator matrix of the code. We next construct the points.
sage: singular.eval("def R = HC[1][5];")
'// ** redefining R **'
sage: singular.eval("setring R;")
''
sage: print singular.eval("POINTS;")
[1]:
[1]:
0
[2]:
1
[3]:
0
[2]:
[1]:
0
[2]:
1
[3]:
1
[3]:
[1]:
0
[2]:
0
[3]:
1
[4]:
[1]:
(a+1)
[2]:
(a)
[3]:
1
...
plus 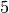 more, for a total of
more, for a total of 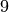 rational points
on the curve. We define our “evaluation divisor”
rational points
on the curve. We define our “evaluation divisor” 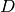 using
a subset of these points (all but the first):
using
a subset of these points (all but the first):
sage: singular.eval("def ER = HC[1][4];")
''
sage: singular.eval("setring ER;")
''
sage: # D = sum of the rational places no. 2..9 over F_4
sage: singular.eval("intvec D = 2..9;")
''
sage: # let us construct the corresponding evaluation AG code :
sage: print singular.eval("matrix C = AGcode_L(G,D,HC);")
Forms of degree 3 :
10
<BLANKLINE>
Vector basis successfully computed
<BLANKLINE>
sage: # here is a linear code of type [8,5,> = 3] over F_4
sage: print singular.eval("print(C);")
0,0,(a+1),(a), 1, 1, (a), (a+1),
1,0,(a), (a+1),(a),(a+1),(a), (a+1),
1,1,1, 1, 1, 1, 1, 1,
0,0,(a), (a+1),1, 1, (a+1),(a),
0,0,1, 1, (a),(a+1),(a+1),(a)
This is, finally, our desired generator matrix, where a
represents a generator of the field extension of degree 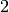 over the base field
over the base field 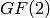 .
.
Can this be “wrapped”?