For any congruence subgroup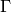 
, the direct sum
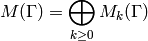
is a ring, since the product of modular forms
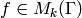and 
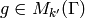is
an element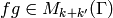 
. Sage can compute
likely generators for rings of modular forms, but currently doesn’t
prove any of these results.
We verify the statement proved in Serre’s “A Course in Arithmetic”
that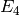 
and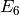 
generate the space of level
one modular forms.
sage: ModularFormsRing(SL2Z).generators(prec=4)
[(4, 1 + 240*q + 2160*q^2 + 6720*q^3 + O(q^4)),
(6, 1 - 504*q - 16632*q^2 - 122976*q^3 + O(q^4))]
Have you ever wondered which forms generate the ring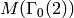 
? It
turns out that one form of weight 2 and one form of weight 4 suffice.
sage: ModularFormsRing(Gamma0(2)).generators(prec=12)
[(2, 1 + 24*q + 24*q^2 + 96*q^3 + 24*q^4 + 144*q^5 + 96*q^6 + 192*q^7 + 24*q^8 + 312*q^9 + 144*q^10 + 288*q^11 + O(q^12)),
(4, 1 + 240*q^2 + 2160*q^4 + 6720*q^6 + 17520*q^8 + 30240*q^10 + O(q^12))]
Here’s generators for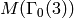 
. Notice that
elements of weight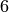 
are now required, in addition to
weights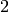 
and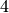 
.
sage: ModularFormsRing(Gamma0(3)).generators()
[(2, 1 + 12*q + 36*q^2 + 12*q^3 + 84*q^4 + 72*q^5 + 36*q^6 + 96*q^7 + 180*q^8 + 12*q^9 + O(q^10)),
(4, 1 + 240*q^3 + 2160*q^6 + 6720*q^9 + O(q^10)),
(6, q - 6*q^2 + 9*q^3 + 4*q^4 + 6*q^5 - 54*q^6 - 40*q^7 + 168*q^8 + 81*q^9 + O(q^10))]
We can also handle rings of modular forms for odd congruence subgroups, but
with the usual caveat that we can’t calculate forms of weight 1. So these are
elements generating the graded ring of forms of weight 0 or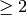 
.
sage: ModularFormsRing(Gamma1(3)).generators()
[(2, 1 + 12*q + 36*q^2 + 12*q^3 + 84*q^4 + 72*q^5 + 36*q^6 + 96*q^7 + 180*q^8 + 12*q^9 + O(q^10)),
(3, 1 + 54*q^2 + 72*q^3 + 432*q^5 + 270*q^6 + 918*q^8 + 720*q^9 + O(q^10)),
(3, q + 3*q^2 + 9*q^3 + 13*q^4 + 24*q^5 + 27*q^6 + 50*q^7 + 51*q^8 + 81*q^9 + O(q^10)),
(4, 1 + 240*q^3 + 2160*q^6 + 6720*q^9 + O(q^10))]
-series