Some Common Issues with Functions

Some aspects of defining functions (e.g., for differentiation or plotting) can be confusing. In this section we try to address some of the relevant issues.

Here are several ways to define things which might deserve to be called “functions”:

1. Define a Python function, as described in Functions, Indentation, and Counting. These functions can be plotted, but not differentiated or integrated.

sage: def f(z): return z^2
sage: type(f)
<type 'function'>
sage: f(3)
9
sage: plot(f, 0, 2)

In the last line, note the syntax. Using plot(f(z), 0, 2) instead will give an error, because z is a dummy variable in the definition of f and is not defined outside of that definition. Indeed, just f(z) returns an error. The following will work in this case, although in general there are issues and so it should probably be avoided (see item 4 below).

sage: var('z')   # define z to be a variable
z
sage: f(z)
z^2
sage: plot(f(z), 0, 2)

At this point, f(z) is a symbolic expression, the next item in our list.

2. Define a “callable symbolic expression”. These can be plotted, differentiated, and integrated.

sage: g(x) = x^2
sage: g        # g sends x to x^2
x |--> x^2
sage: g(3)
9
sage: Dg = g.derivative(); Dg
x |--> 2*x
sage: Dg(3)
6
sage: type(g)
<type 'sage.symbolic.expression.Expression'>
sage: plot(g, 0, 2)

Note that while g is a callable symbolic expression, g(x) is a related, but different sort of object, which can also be plotted, differentated, etc., albeit with some issues: see item 5 below for an illustration.

sage: g(x)
x^2
sage: type(g(x))
<type 'sage.symbolic.expression.Expression'>
sage: g(x).derivative()
2*x
sage: plot(g(x), 0, 2)

3. Use a pre-defined Sage ‘calculus function’. These can be plotted, and with a little help, differentiated, and integrated.

sage: type(sin)
<class 'sage.functions.trig.Function_sin'>
sage: plot(sin, 0, 2)
sage: type(sin(x))
<type 'sage.symbolic.expression.Expression'>
sage: plot(sin(x), 0, 2)

By itself, sin cannot be differentiated, at least not to produce cos.

sage: f = sin
sage: f.derivative()
...
AttributeError: ...

Using f = sin(x) instead of sin works, but it is probably even better to use f(x) = sin(x) to define a callable symbolic expression.

sage: S(x) = sin(x)
sage: S.derivative()
x |--> cos(x)

Here are some common problems, with explanations:

4. Accidental evaluation.

sage: def h(x):
...       if x<2:
...           return 0
...       else:
...           return x-2

The issue: plot(h(x), 0, 4) plots the line 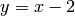, not the multi-line function defined by h. The reason? In the command plot(h(x), 0, 4), first h(x) is evaluated: this means plugging x into the function h, which means that x<2 is evaluated.

sage: type(x<2)
<type 'sage.symbolic.expression.Expression'>

When a symbolic equation is evaluated, as in the definition of h, if it is not obviously true, then it returns False. Thus h(x) evaluates to x-2, and this is the function that gets plotted.

The solution: don’t use plot(h(x), 0, 4); instead, use

sage: plot(h, 0, 4)

5. Accidentally producing a constant instead of a function.

sage: f = x
sage: g = f.derivative()
sage: g
1

The problem: g(3), for example, returns an error, saying “ValueError: the number of arguments must be less than or equal to 0.”

sage: type(f)
<type 'sage.symbolic.expression.Expression'>
sage: type(g)
<type 'sage.symbolic.expression.Expression'>

g is not a function, it’s a constant, so it has no variables associated to it, and you can’t plug anything into it.

The solution: there are several options.

• Define f initially to be a symbolic expression.

sage: f(x) = x        # instead of 'f = x'
sage: g = f.derivative()
sage: g
x |--> 1
sage: g(3)
1
sage: type(g)
<type 'sage.symbolic.expression.Expression'>

• Or with f as defined originally, define g to be a symbolic expression.

sage: f = x
sage: g(x) = f.derivative()  # instead of 'g = f.derivative()'
sage: g
x |--> 1
sage: g(3)
1
sage: type(g)
<type 'sage.symbolic.expression.Expression'>

• Or with f and g as defined originally, specify the variable for which you are substituting.

sage: f = x
sage: g = f.derivative()
sage: g
1
sage: g(x=3)    # instead of 'g(3)'
1

Finally, here’s one more way to tell the difference between the derivatives of f = x and f(x) = x

sage: f(x) = x
sage: g = f.derivative()
sage: g.variables()  # the variables present in g
()
sage: g.arguments()  # the arguments which can be plugged into g
(x,)
sage: f = x
sage: h = f.derivative()
sage: h.variables()
()
sage: h.arguments()
()

As this example has been trying to illustrate, h accepts no arguments, and this is why h(3) returns an error.